Рулевой привод с жесткой обратной связью.

Жесткая обратная связь обеспечивает пропорциональность угла отклонения руля величине управляющего сигнала и слабую зависимость этого отклонения от шарнирного момента. Сигнал, пропорциональный углу отклонения руля, при помощи обратной связи сравнивается с управляющим сигналом. В качестве элемента обратной связи может быть использован потенциометрический датчик, измеряющий угол отклонения руля. На рис.2 показана структурная схема рулевого привода с жесткой обратной связью.

Рис.2. Структурная схема рулевого привода с жесткой обратной связью.

Передаточная функция рулевого привода:

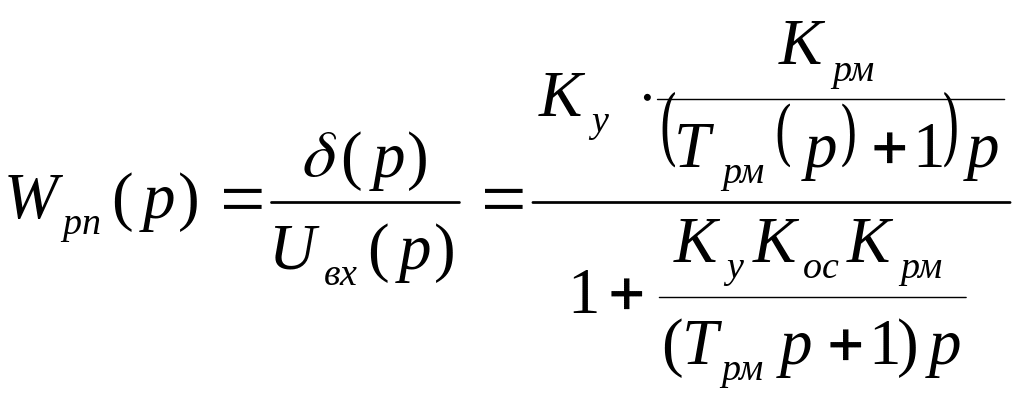
или

где - постоянная времени рулевого привода,

- степень затухания колебаний рулевого привода,

-коэффициент передачи рулевого привода,

Введение жесткой обратной связи, кроме обеспечения пропорциональности угла отклонения руля величине управляющего сигнала, снижает постоянную времени рулевого привода, т. е. увеличивает его быстродействие. Частота собственных колебаний рулевого привода должна быть примерно на порядок выше частоты угловых колебаний ЛА.

Синтез системы.

Составим разомкнутую структурную схему рулевого привода с жесткой обратной связью и определим значения коэффициентов.

Рис.3. Структурная схема разомкнутой системы рулевого привода

Для определения коэффициента К_у смоделируем структурную схему разомкнутой системы рулевого привода с жесткой обратной связью в программной среде MathLab.

Рис.4. Структурная схема разомкнутой системы рулевого привода с жесткой обратной связью в среде MathLab

Приведем ЛАФЧХ разомкнутой системы рулевого привода с жесткой обратной связью при значении коэффициентов К_у=10 и К_рм=10:

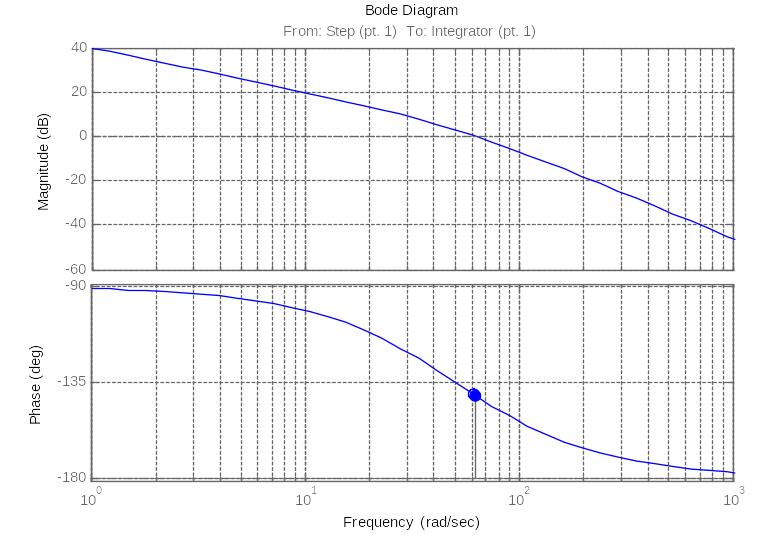
Рис.5. ЛАФЧХ разомкнутой системы рулевого привода.

Из графика видно, что при значении коэффициентов К_у=10 и К_рм=10 запас по фазе составляет φ=38.7˚. Из этого следует, что данная система устойчива.

Составим структурную схему замкнутой системы рулевого привода с жесткой обратной связью:

Рис.6. Структурная схема замкнутой системы рулевого привода с жесткой ОС.

Составим структурную схему замкнутой системы рулевого привода с жесткой обратной связью в программной среде MathLab.

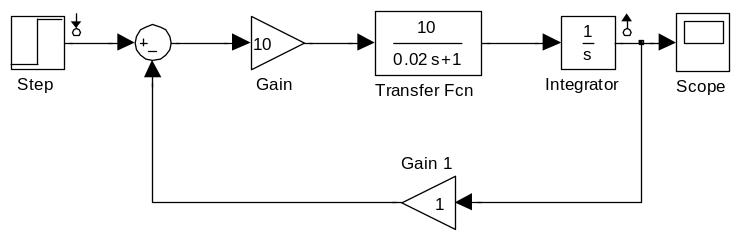
Рис.7. Структурная схема замкнутой системы рулевого привода с жесткой обратной связью.

График переходного процесса в замкнутом рулевом приводе с жесткой обратной связью имеет вид при значении коэффициентов

Рис.8. Переходный процесс замкнутой системы рулевого привода

Из графика видно, что время переходного процесса в замкнутом рулевом приводе с жесткой обратной связью при значении составляет 0,155с.

Таким образом, при Ку=10, К_р.м.=10 и Т_р.м.=0.02 мы получили постоянную времени рулевого привода равной Т_р.п.=0.014.

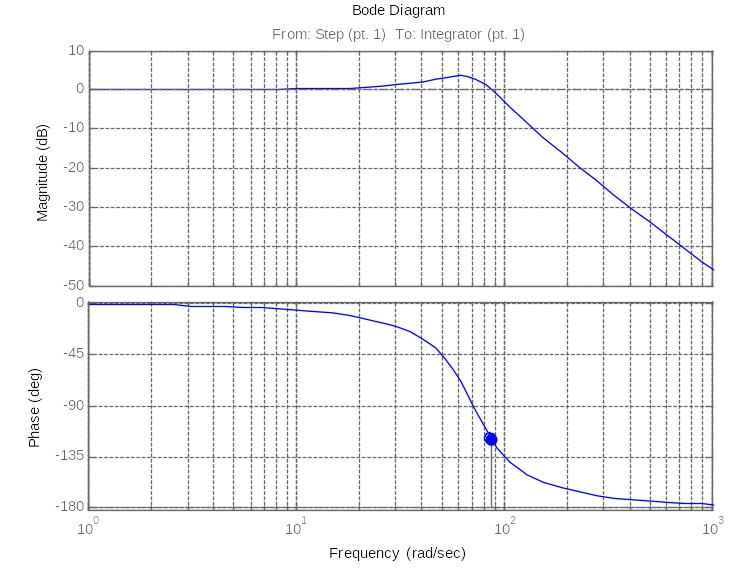
Рис.9. ЛАФЧХ замкнутой системы рулевого привода с жесткой ОС

Структурная схема системы ла – ап

Законом управления или регулирования называют простейшее уравнение, отображающее наиболее существенные связи и преобразования, реализуемые автопилоты.

В соответствии с заданием закон управления автопилотом с управлением по углу и с жесткой обратной связью рулевого привода имеет вид:

где ; .

Составим структурную схему разомкнутой системы управления автопилотом:

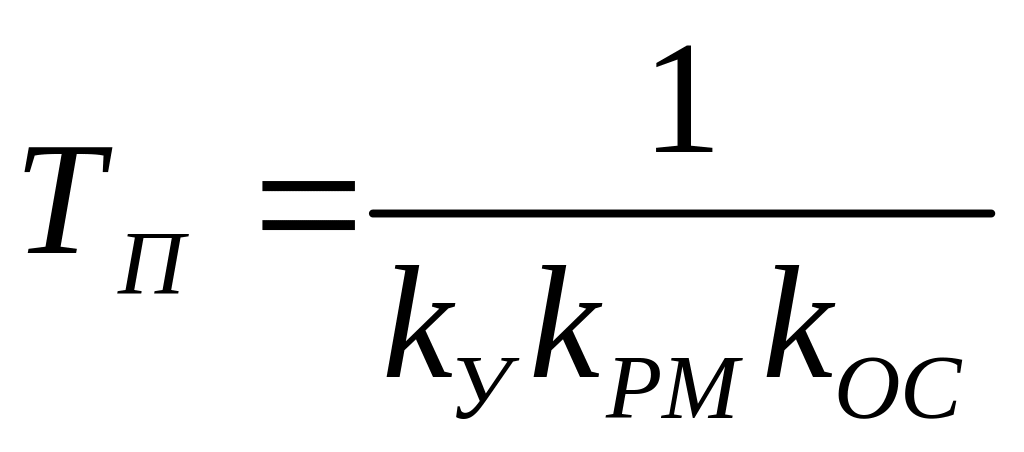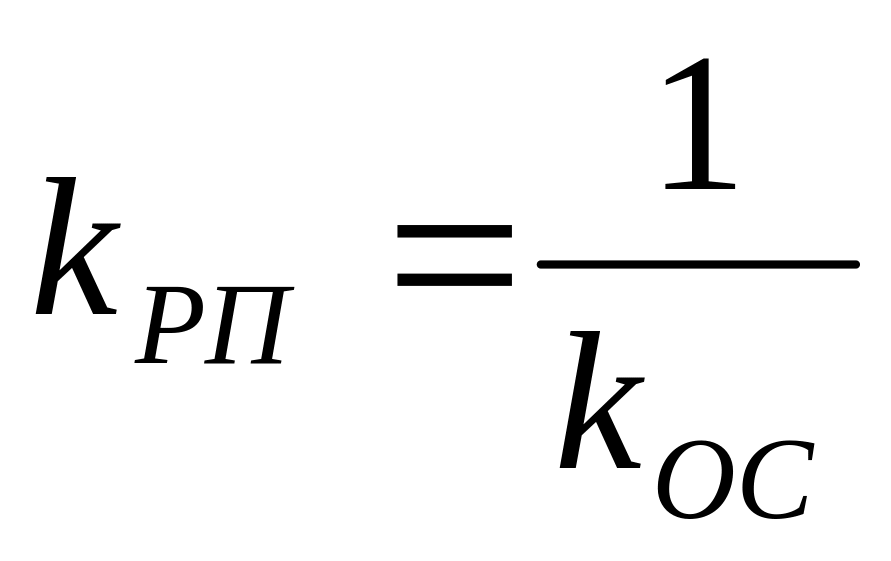Рис. 10. Структурная схема разомкнутой системы управления автопилотом

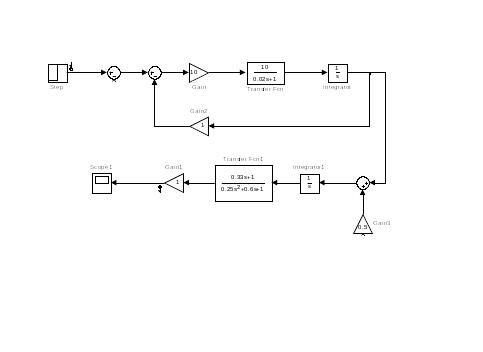
Рис. 11. Структурная схема разомкнутой системы управления автопилотом в среде MathLab

Приведем ЛАФЧХ разомкнутой системы управления автопилотом:

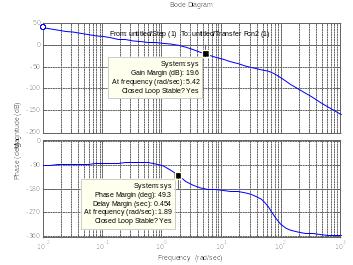
Рис. 12. ЛАФЧХ разомкнутой системы управления автопилотом

При значении коэффициента, Ку =1 запас по фазе составляет Δφ=49,3˚, а запас по амплитуде ΔL =19.6 Дб.

Для обеспечения необходимых запасов по фазе и амплитуде вводим корректирующее звено .

Составим разомкнутую систему управления автопилотом с корректирующим звеном:

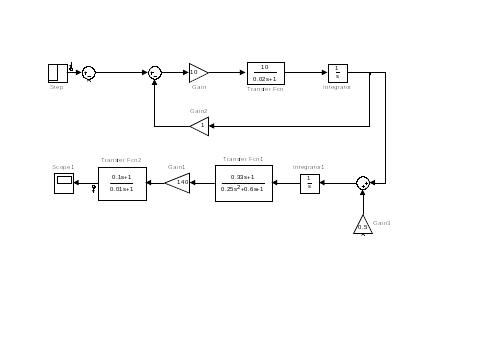
Рис. 13. Структурная схема разомкнутой системы управления автопилотом с корректирующим звеном в среде MathLab

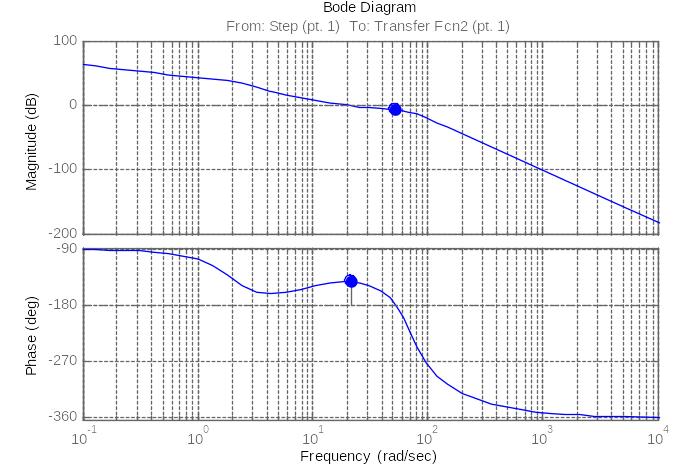
Рис. 14. ЛАФЧХ разомкнутой системы управления автопилотом

Из графика видно, что при значении коэффициентов Ку = Крм. =10 запас по фазе составляет 38°, амплитуда – 6,82 дБ.

Составим структурную схему замкнутой системы по отношению к внешнему управляющему моменту и построим ЛАФЧХ и график переходного процесса этой системы.

Структурная схема замкнутой системы по отношению к внешнему управляющему моменту показана на рис 15.

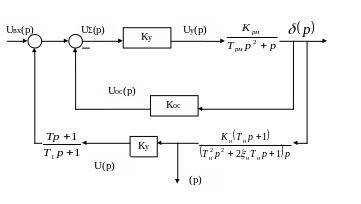
Рис. 15. Структурная схема замкнутой системы управления автопилотом по отношению к внешнему управляющему моменту

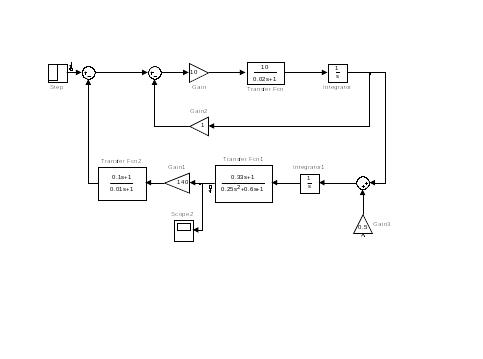
Рис.16. Структурная схема замкнутой системы управления автопилотом по отношению к внешнему управляющему моменту в среде MathLab.

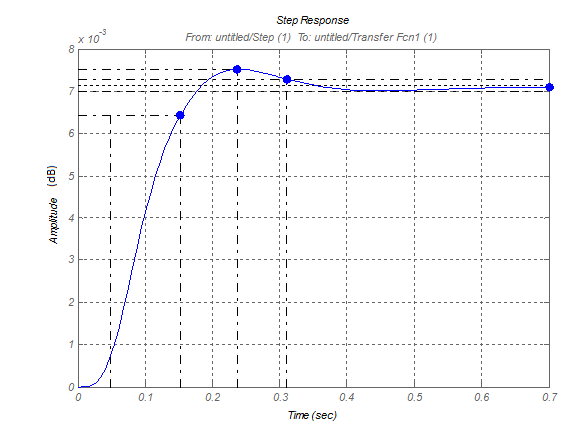
Рис.15. Переходный процесс замкнутой системы по управляющему воздействию.

Из графика видно, что:

Время переходного процесса – 0,311с.

Время нарастания – 0,104с.

Величина перерегулирования – 5,3%

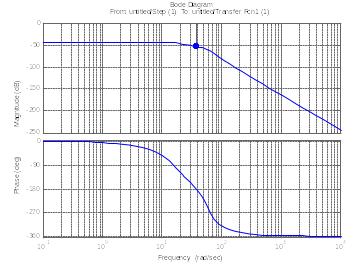
Рис.16. ЛАФЧХ замкнутой системы по управляющему воздействию.

Составим структурную схему замкнутой системы по отношению к внешнему возмущающему моменту и построим ЛАФЧХ и график переходного процесса этой системы.

Структурная схема замкнутой системы по отношению к внешнему управляющему моменту показана на рис 17:

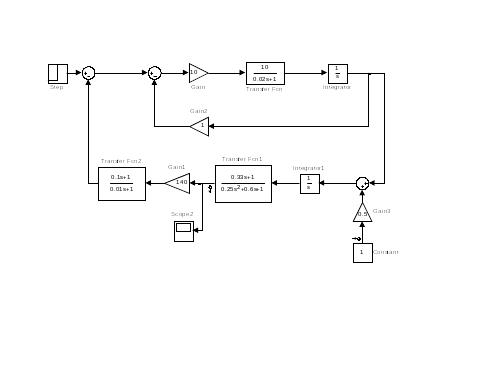
Рис. 17. Структурная схема замкнутой системы управления автопилотом по отношению к внешнему возмущающему моменту в среде MathLab

Построим график переходного процесса замкнутой системы по отношению к внешнему возмущающему моменту.

Рис.18. Переходный процесс замкнутой системы по возмущающему воздействию.

Из графика видим, что:

Время переходного процесса – 0,301с.

Время нарастания – 0,112с.

Величина перерегулирования – 4,79%

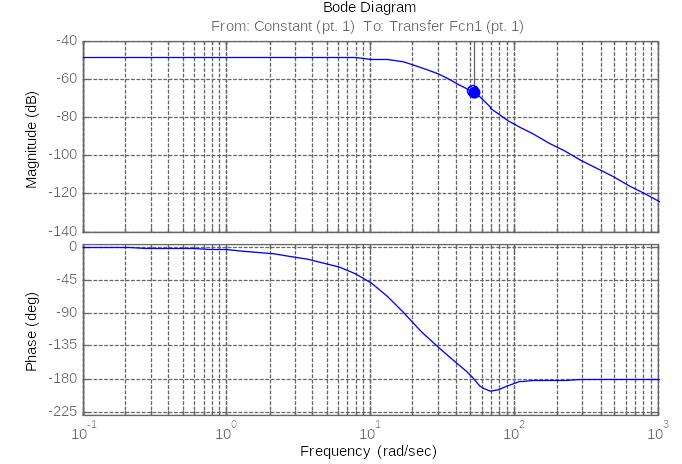
Рис.19. ЛАФЧХ замкнутой системы по возмущающему воздействию

Вывод.

В процессе выполнения работы по синтезу системы угловой стабилизации дозвукового транспортного самолета по заданному курсу была составлена схема сил и моментов, действующих на объект, составлена система уравнений «система угловой стабилизации - транспортный самолет», линеаризована эта система, составлены структурные схемы и получены передаточные функции разомкнутой и замкнутой системы. Методом ЛАФЧХ исследована устойчивость объекта, определено значение общего коэффициента усиления по контуру, при котором система имеет необходимые запасы устойчивости по амплитуде и фазе. Для обеспечения необходимых запасов по фазе и амплитуде ввели корректирующее звено. Построена ЛАФЧХ разомкнутой системы. Построена ЛАФЧХ замкнутой системы по отношению к внешнему возмущающему моменту. Построена ЛАФЧХ замкнутой системы по отношению к управляющему моменту. Построены графики переходных процессов, как реакции на единичное управляющее и возмущающее воздействие.

На основе полученных результатов и анализа построенных ЛАФЧХ и графиков переходных процессов системы угловой стабилизации дозвукового транспортного самолета по заданному курсу можно сказать, что при подобранных значениях коэффициентов система устойчива, имеет хороший запас по фазе и небольшое время переходных процессов.