7)Сложение двух гармонических колебаний одинакового направления и одной частоты

При сложении двух гармонических колебаний одинакового направления и частоты, результирующее смещение будет суммой ( ) смещений   и  , которые запишутся следующими выражениями:

,  , Сумма двух гармонических колебаний также будет гармоническим колебанием той же круговой частоты:   =   . Значения амплитуды А и начальной фазы φ этого гармонического колебания будет зависеть от амплитуд исходных колебаний и их начальных фаз (Рис. 1.2).

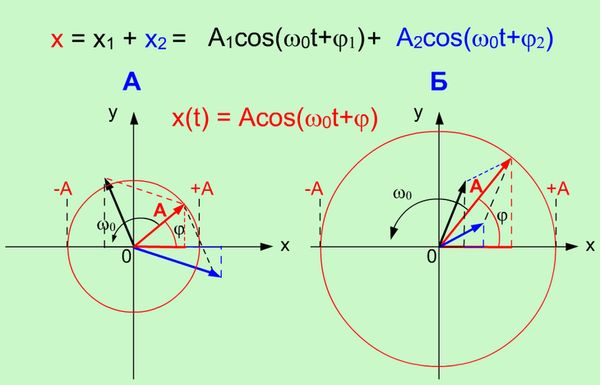
Рисунок 1.2. Сложение двух гармонических колебаний одинакового направлени частоты

На рисунке 1.2. приведено два примера А и В сложения гармонических колебаний с использованием метода векторных диаграмм. Из векторных диаграмм видно, что направление (начальная фаза φ) и длина А вектора амплитуды суммарного гармонического колебания зависит, как от направления (от начальных фаз), так и от длины векторов амплитуд исходных гармонических колебаний.  Если угол (разность фаз: Δφ = φ1 - φ2) между векторами А1 и А2 равен 0, то исходные колебания находятся в фазе и суммарная амплитуда (А =А1 +А2) будет максимальна. Если угол (разность фаз: Δφ = φ1 - φ2) между векторами А1 и А2 равен - π или π, то исходные колебания находятся в противофазе и суммарная амплитуда (А =  А1 -А2 ) будет минимальна.

8)Сложение двух гармонических колебаний с неодинаковыми частотами.(Биения и модуляции)

Если частоты колебаний   и  , неодинаковы, векторы А1 и А2 будут вращаться с различной скоростью. В этом случае результирующий вектор А пульсирует по величине и вращается с не постоянной скоростью. Результирующим движение уже будет не гармоническое колебание, а сложный колебательный процесс.

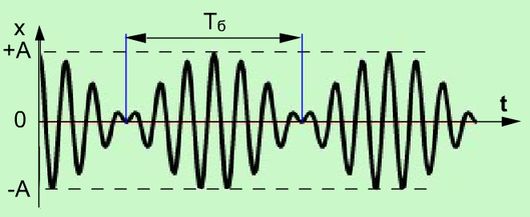
Биения Биения возникают при сложении колебаний, отличающихся по частоте на небольшую величину, и проявляются в появлении более низкочастотных изменений амплитуды суммарного сигнала, по сравнению с исходными частотами. Амплитуда колебаний при этом меняется от минимального значения равного разности исходных амплитуд до максимального значения, равного сумме амплитуд исходных колебаний, и вновь до минимального значения. Периодом биений является время повторения этого процесса (Рис 1.3.).

Рисунок 1.3.

За счет того, что вращение векторов А1 и А2 происходит с близкими, но отличающимися скоростями, разность фаз этих двух колебаний будет не постоянна, а медленно, то увеличиваться, то уменьшаться. Колебания будут находиться, то в фазе, то в противофазе, в результате амплитуда суммарного сигнала тоже будет меняться. Время за которое разность фаз измениться на 2π и будет периодом биений Тб (Тб = 2π/Δω). Δω -разность круговых частот исходных колебаний. Биения применяют при обнаружении металлических предметов мин, оружия и т.д.