4. Переполнение разрядной сетки

При сложении чисел одинакового знака, представленных в форме с фиксированной запятой, может возникнуть переполнение разрядной сетки.

Признак переполнения разрядной сетки сумматора прямого кода - появление единицы переноса из старшего разряда цифровой части числа.

Пример.

1а) А=0,1010 и В=0,1101 2а) А=-0,1100 и В=-0,1010

+ +

1 единица переноса 1 единица переноса

Признак переполнения разрядной сетки сумматора дополнительного кода при сложении положительных чисел - отрицательный знак результата, а при сложении отрицательных чисел - положительный знак результата.

Пример.

3а) А=0,1011 и В=0,1010 4а) А=-0,1011 и В=-0,1001

+ +

3. Признак переполнения разрядной сетки сумматора обратного кода - знак результата, противоположный знакам операндов.

Пример.

5а) А=0,0111 и В=0,1101 6а) А=-0,0110 и В =-0,1101

+ +

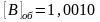
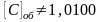
Для обнаружения переполнения разрядной сетки в составе цифрового автомата должны быть предусмотрены аппаратные средства, автоматически вырабатывающие признак переполнения - сигнал .

При умножении любых чисел также может возникнуть переполнение разрядной сетки.

Для обнаружения переполнения разрядной сетки в составе цифрового автомата должны быть предусмотрены аппаратные средства, автоматически вырабатывающие признак переполнения - некий сигнал переполнения.

Один из методов обнаружения переполнения разрядной сетки предполагает ввод вспомогательного разряда в знаковую часть изображения числа, который называют разрядом переполнения. Такое представление числа называют модифицированным.

5. Метод Квайна-Мак-Класски

При проэктировании цифровых автоматов широко используются методы минимизации булевых функций, позволяющие получать рекомендации для построения экономичных схем цифровых автоматов. Общая задача минимизации булевых функций может быть сформулирована следующим образом: найти аналитическое выражение заданной булевой функции в форме, содержащей минимально возможное число букв.

При минимизации по методу Квайна (базис 1) предполагается, что исходная функция задана в СНДФ.

Импликанта функции — некоторая логическая функция, обращаемая в нуль при наборе переменных, на котором сама функция также равна нулю.

Поэтому любой конъюнктивный терм, входящий в состав СНДФ, или группа термов, соединенных знаками дизъюнкции, являются импликантами исходной НДФ.

Первичная импликанта функции — Импликанта типа элементарной конъюнкции некоторых переменных, никакая часть которой уже является импликаитой.

Следует отметить, что в общей постановке данная задача пока не решена, однако достаточно хорошо исследована в классе дизъюнктивно - конъюнктивных форм.

Метод Квайна основывается на применении двух основных соотношений.

Соотношение склеивания

Ах V А/х = Ах V А/х V А,

где А - любое элементарное произведение.

Соотношение поглощения

А~х V А = А,   ~х E {х; /x}.

Справедливость обоих соотношений легко проверяется. Суть метода заключается в последовательном выполнении всех возможных склеиваний и затем всех поглощений, что приводит к сокращенной ДНФ. Метод применим к совершенной ДНФ. Из соотношения поглощения следует, что произвольное элементарное произведение поглощается любой его частью. Для доказательства достаточно показать, что произвольная простая импликанта р = x_i1x_i2 ... x_in может быть получена. В самом деле, применяя к р операцию развертывания (обратную операции склеивания):

A = A (x v /x) = Ax v A/x

по всем недостающим переменным x_i^(k+l), ..., X_i^n исходной функции f, получаем совокупность S конституент единицы. При склеивании всех конституент из S получим импликанту р. Последнее очевидно, поскольку операция склеивания обратна операции развертывания. Множество S конституент обязательно присутствует в совершенной ДНФ функции f поскольку р - ее импликанта.

Метод представляет собой формализованный на этапе нахождения простых импликант метод Квайна. Формализация производится следующим образом:

Все конституанты единицы из СДНФ булевой функции f записываются их двоичными номерами.

Все номера разбиваются на непересекающиеся группы. Признак образования i-й группы: i единиц в каждом двоичном номере конституенты единицы.

Склеивание производят только между номерами соседних групп. Склеиваемые номера отмечаются каким-либо знаком (зачеркиванием).

Склеивания производят всевозможные, как и в методе Квайна. Неотмеченные после склеивания номера являются простыми импликантами.

Нахождение минимальных ДНФ далее производится по импликантной матрице.

Пример (+Методичка по дискретной математике)