
Оглавление
1) Формы представления чисел 2
2) Представление отрицательных чисел 3
3) Сложение чисел, представленных в форме с фиксированной точкой, на двоичных сумматорах 4
4) Переполнение разрядной сетки 6
5) Метод Квайна-Мак-Класски 7
6) Метод карт Карно 8
7) Логические операторы электронных схем 9
8) Последовательностные автоматы 11
Формы представления чисел
Внутри ЭВМ информация всегда представляется в виде чисел, записанных в той или иной системе счисления.
Система счисления — совокупность приемов и правил для записи чисел цифровыми знаками или символами. Наиболее известна десятичная система счисления, в которой для записи чисел используются цифры 0, 1, ..., 9.
Двоичная система счисления — система счисления, в которой для изображения чисел используются два символа.
Представление чисел с фиксированной запятой (точкой). Естественная форма представления числа в цифровом автомате характеризуется тем, что положение его разрядов в автоматном изображении остается всегда постоянным независимо от величины самого числа.
Чтобы упростить функционирование цифрового автомата, необходимо ограничить входную информацию какой-то одной областью чисел (на вход автомата желательно подавать либо целые числа, либо правильные дроби, либо любые числа), что позволит определить значения масштабного коэффициента Ка. Например, если на вход цифрового автомата поступало только правильные дроби, то -1<[Aф]<1
где [Aф] — машинное изображение числа для формы представления с фиксированной запятой. Тогда число А будет представлено в виде А = [Aф]* Кa .
Величина масштабного коэффициента Кa, удовлетворяющего условию (3.19), определяет тот факт, что в машинном изображении запятая все гда стоит тюсле целой части дроби, т. е. перед ее старшим разрядом. Следовательно, можно хранить только дробную часть числа (цифровую часть), а в разряде целой части писать дополнительную информацию.
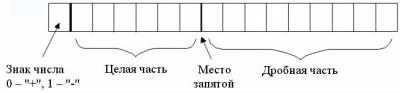
В форме с ФЗ в разрядной сетке выделяется строго определенное число разрядов для целой и для дробной частей числа. Левый (старший) разряд хранит признак знака (0 – "+", 1 – "-") и для записи числа не используется.
Представление чисел в форме с плавающей запятой. [A] =m•2P, где m - мантисса (|m|<1), а р – порядок (целое число). В разрядной сетке выделяется определенное количество разрядов для хранения мантиссы и порядка с их знаками. Основание системы счисления (2) нигде не хранится, но используется при вычислениях.

Существуют форматы с другим размещением мантиссы и порядка в разрядной сетке.
Для каждого числа существует множество нормальных форм:
0,25 = 0,25•100= 0,025•101 = 0,0025•102
При увеличении порядка происходит сдвиг мантиссы вправо, младшие разряды могут выйти за пределы разрядной сетки, что уменьшит точность представления чисел. Поэтому для представления чисел с ПЛЗ используется нормализованная форма записи, когда первая цифра мантиссы должна быть обязательно значащей. (двоичная единица):

Представление отрицательных чисел
Один из способов выполнения операции вычитания – замена знака вычитаемого на противоположный и прибавление его к уменьшаемому: А-В=А+(-В)
Таким образом операцию арифметического вычитания заменяют операцией алгебраического сложения, которая и становится основной операцией в ЭВМ.
Для машинного представления отрицательных чисел используют прямой, дополнительный и обратный коды.
Прямой код – это представление числа в двоичной системе счисления, при котором первый (старший) разряд отводится под знак числа. Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1. (0 00011010 - положительное число, 1 00011010 – отрицательное число)
Обратный код – Обратный n-разрядный двоичный код положительного целого числа состоит из одноразрядного кода знака (двоичной цифры 0), за которым следует n-1-разрядное двоичное представление модуля числа (обратный код положительного числа совпадает с прямым кодом).(Пример. Двоичное представление числа 5 есть 101. Обратный 10-разрядный двоичный код числа +5 записывается как 0000000101.)
Обратный n-разрядный двоичный код отрицательного целого числа состоит из одноразрядного кода знака (двоичной цифры 1), за которым следует n-1-разрядное двоичное число, представляющее собой инвертированное n-1-разрядное представление модуля числа. Следует отметить, что для изменения знака числа достаточно проинвертировать все его разряды не обращая внимания знаковый ли это разряд или информационные.
Для преобразования отрицательного числа в положительное тоже применяется операция инвертирования. Этим обратные коды удобны в применении. В качестве недостатка следует отметить, что в обратных двоичных кодах имеются два кода числа 0: «положительный нуль» 0000000000 и «отрицательный нуль» 1111111111 (приведены 10-разрядные обратные коды). Это приводит к некоторому усложнению операции суммирования. Поэтому в дальнейшем перешли к дополнительным кодам записи знаковых целых чисел.
Дополнительный код отрицательного числа можно получить инвертированием модуля двоичного числа (первое дополнение) и прибавлением к инверсии единицы (второе дополнение)
Дополнительный код — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ.
