1. Определение модели, понятие о моделировании.

Модель – с французского образ. Моделирование это процесс построения и изучения модели в целях получения новых знаний, то есть исследуемый объект и его модель могут быть любой природы. Модели могут быть предметными и идеальными(мысленными).

2. Классификация моделей

1 тип - Под предметной моделью понимается некоторый материальный объект отражающий свойства исследуемого объекта и способный заменить его в процессе эксперимента. Предметные модели применяются в тех случаях когда нужно изучить только некоторые особенности: геометрические, гидравлические характеристики при изменении условий эксплуатаций. В настоящее время это моделирование применяется либо в учебных целях, либо в особо ответственных моментах. Предметные модели бывают: пространственно-временные(геометрические), физические.

2 тип – предметно-математический – это модели на уровне математических уравнений описывающих процессы на объекте и модели. Обычно конструируются из иной физической природы элементов, чем исследуемый объект, но процессы в них описываются одними и теми же математическими уравнениями. Преимущество над предметными моделями: 1дешевле в 100 или 1000раз. 2 не требуют разрушения при построении новой модели. 3 могут быстро переналаживаться.

3 тип – идеальные модели – существуют в голове исследователя в виде образов(знаковые модели). Под математической моделью понимается совокупность математических и логических связей при помощи которых устанавливаются связи между исследуемым объектом и окружающей средой. Все математические модели гидравлических процессов можно разделить: 1 пространственные 2 по глубине. Могут быть с распределенными параметрами то есть параметры модели зависят от координат и с сосредоточенными параметрами когда в результате осреднения весь бассейн стягивается в одну точку. Модели с распределенными параметрами обычно применяются когда нужно описать процесс по территории всего бассейна. С сосредоточенными – когда нужна одна характеристика. Модели могут быть трех мерными а если модель имеет время то ее называют динамической.

Все эти модели могут быть стахостическими и детерменестическими(ее вид у=f(x)) они могут быть динамическими. Для описания стахостического процесса требуется коласальный объем данных за наблюдаемым процессом.

Динимако-стахостические модели – это когда на детерменестическую модель вводится случайная составляющая.

4 тип – физико-статистические модели – это модели в основе которых лежат строгие физические законы а параметры модели находятся по результатам наблюдений и обрабатываются статистически.

3. Линейная парная регрессия.

Yx=a₀+a₁x

S=∑(y- a₀+a₁x)²→min

Рассматривая S в качестве функции параметров а₀ и а₁ и проведя дифференцирование получаем

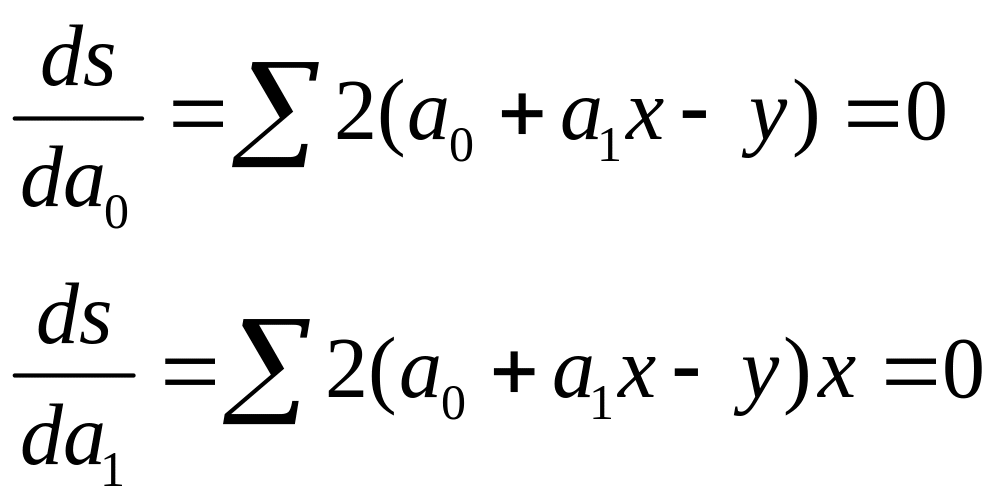
Откуда система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет слудующий вид:

na₀+a₁∑x=∑y

a₀∑x+a₁∑x²=∑xy

4. Нелинейная парная регрессия.

Y_x=a₀+a₁x+a₂x²

Значение величин ХУ представлены двумя рядами данных, если бы все значения полученные по данным наблюдения лежали бы строго на кривой, описываемой уравнением параболы то не существовало бы ни каких проблем однако на практике имеем разность между данными наблюдения и данными полученными по уравнению связи эта разность как раз и появляется в силу наличия ошибок упрощения, поэтому возникает проблема нахождения таких коэффициентов регрессии, при которых ошибка была бы минимальной. Оптимальным является оценка ошибки по методу наименьших квадратов.

S=∑(y-a₀-a₁x-a₂x²)²→min

Для нахождения значений неизвестных коэффициентов при которых функция была бы минимальной необходимо приравнять частное производное по этим величинам к нулю.

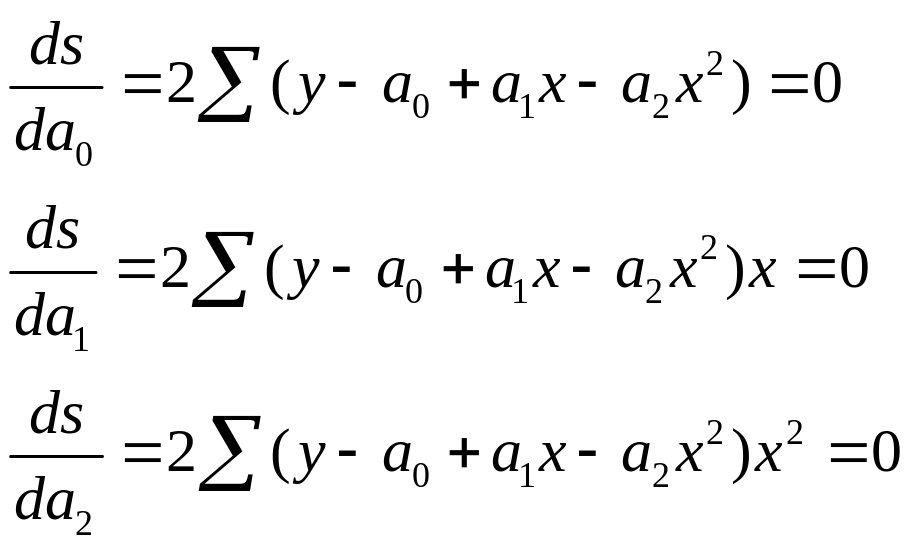
Проделав простейшие преобразования получим систему нормальных уравнений.

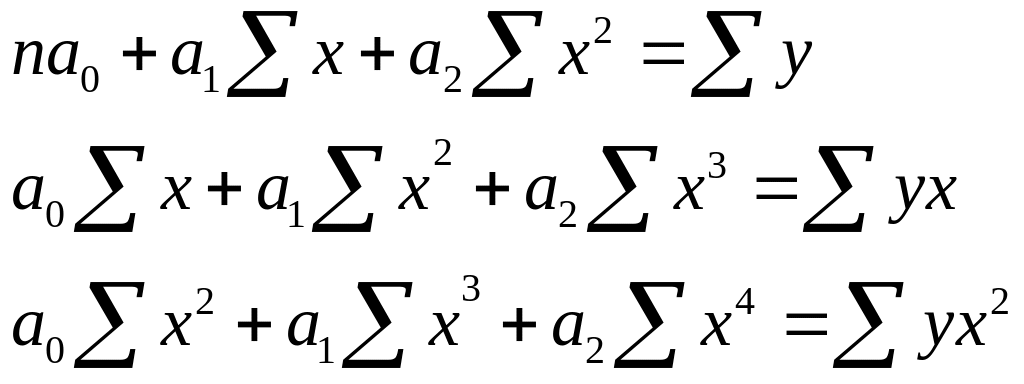
Решив систему найдем значения неизвестных коэффициентов а0, а1, а2 и получим уравнение регрессии.