1. Бінарныя дачыненні. Дачыненне эквівалентнасці і падзелы на класы.

Азн.Няхай А і В . уласцівасць ρ (a, b), і , тады кажуць, што зададзена бінарнае дачыненне паміж мноствамі А і В.

Пр. a/ b – цотны лік,

Абсяг вызн. і абсяг знач. = АхВ.

Далей будзем разглядаць бін дач на мн-ве А ( )

Азн.: 1. a ρ a, - рэфлексіўнасць.(a a)

2. , - антырэфлексіўнасць. (a>a)

3. a ρ b, то b ρ a , - сіметрычнасць.(a, b – цот)

4. , - антысіметрычнасць.

5. a ρ b і b ρ a, то a=b, - асіметрычнасць.( a b і b a, то a=b)

6. a ρ b і b ρ c, то a ρ c, - транзітыўнасць.(a>b, b>c, то a>c)

Азн. Дачыненне ρ - дачыненне эквівалентнасці, калі яно рэфлексіўнае, сіметрычнае, транзітыўнае. Абазн .

Напр. =,||, раўназначнасць, падабенства.

Азн. Няхай на мностве Х зададзена дачыненне эквівал ρ мн-ва усіх элементау мн-ва Х, якія эквівалентны элем х, наз классам эквівалентнасці х (адносна дачынення ρ) і абазн , , .

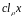Сцв. 1. (рэфлекс)

2.

3.

Д-з 3: , ( транзітыунасць)

транзіт .

Аналаг

Азн. Калі зададзена не пустое мн-ва Х і с-ма яго падмн-вау , дзе , і такіх, што і тады, калі , тады кажуць, што зедадзена разбіцце мн-ва Х.

Т-ма. З кожнай эквівалентнасцю ρ на А звязана разбіцце мноства А на класы і гэтымі класамі будуць усе розныя класы ρ-эквівалентеасці.

Д-з. Адносіна ρ на А валодае ўласцівасцямі рэфлексіўнасці, сіметрычнасці, транзітыўнасці.

маем а ρ а, зн. ,

Калі Ø, то .

Дап. што , тады і , г.зн. с ρ а і с ρ в - сіметр. Т.я. ρ - сіметр. і транзітыўна, то атр-ца а ρ с і с ρ в →а ρ в.

Няхай і а ρ в →х ρ в, таму . Т.ч. . Аналагічна паказваецца і адваротнае , зн. .

З даказанага вынікае, што калі Ø. Т.ч. робім выснову: усе розныя класы ρ-эквівалентнасці ствараюць разбіцце мноства А.

2. Кольца. Прыклады кольцаў. Найпрасцейшыя ўласцівасці кальца. Падкольца. Гомамарфізмы і ізамарфізмы кольцаў.

Азн. Няхай К на якім зададзена + і * . - зададзена кольца, калі:

1. +асац. (а+в)+с=а+(в+с)

2. 

3. 

4. камутат

5. * асац (ав)с=а(вс)

6. дыстрыбут. (а+в)с=ас+вс

7. с(а+в)=са+св.

Прыклады кольцаў: Z, Q, R, C, F, P[x], L, P^∞, Z_m.

Азн. Калі аперацыя + камутат-ая у кольцы, тады кольца наз камутат-ым.

Азн. Калі К камутат-ае кольца з 1, , то К – поле.

Прасцейшыя ўласцівасці кальца:

1. калі існуе нейтральны, то ен адзіны.

2. калі існуе працілеглы, то ен адзіны.

3. у кальцы К а*0=0*а=0

4. (-а)*в=-(ав)

5. (-а)*(-в)=ав

6. (а-в)с=ас-вс, а-в=а+(-в).

Азн. Няхай і . Калі - з’яуляецца кольцам адносна аперацый якія у , тады наз падкальцом кольца .

Прыкл. : .

Азн. Няхай дадзена 2 кольца і Адл-не f: наз гамамарфізмам кольцау, калі яно захоувае абедзве аперацыіі.

1. f(a+b)= f(a) f(b)

2. f(ab)= f(a) f(b).

Азн. Біектыўны гамамарфізм f: K→K^/ наз ізамарфізмам кальца К на К^/.

Азн. - ідэал , калі падкольца і і .

Крытэрый ідэала: Калі і , тады .

Лема(сумежн класау) .

Ул-ць: - кольца, яно наз фактаркольца кольца па ідэалу .