Розділ 6. Визначений інтеграл та його застосування

Тема 6.1. Визначений інтеграл та його обчислення

Мета. Дати поняття визначеного інтегралу, інтегралу по змінній верхній межі, ознайомитись з основними методами обчислення визначених інтегралів.

План.

1. Задачі, що приводять до поняття визначеного інтегралу.

2. Поняття визначеного інтегралу та його властивості.

3. Інтеграл по змінній верхній межі. Теорема про середнє. Формула Ньютона- Лейбніца.

4. Основні методи обчислення визначених інтегралів.

1. Розглянемо задачу про знаходження площі криволінійної трапеції. Якщо на площині задано фігуру, обмежену прямими x=a, x=b, віссю Ox і графіком деякої функції y=f(x), то така фігура називається криволінійною трапецією.

Для того, щоб знайти її площу, розіб’ємо відрізок [a,b] на n частин (надалі будемо казати, що зроблено T- розбиття). Побудуємо через кожну точку T- розбиття пряму паралельну до осі Oy до перетину її з графіком функції y=f(x). Позначимо точки T- розбиття як x₀, x₂, …, x_n, де x₀=a, x_n=b. Довжини відрізків, отриманих при T- розбитті, позначимо x_i, де x_i=x_i-x_i-1, i=1,2,…,n. Виберемо на кожному з відрізків T- розбиття деяку точку в якій функція приймає найменше значення на відрізку x_i і другу точку в якій функція приймає найбільше значення на цьому відрізку. Побудуємо через ці точки відрізки паралельні осі Ox до перетину з першим вертикальним відрізком. Ясно, що площа трапеції більша або рівна суми площ прямокутників, побудованих через точки мінімуму але менша або рівна суми площ прямокутників, побудованих через точки максимуму, тобто

. (1)

Надалі будемо вибирати таке T- розбиття, щоб довжина максимального його відрізка прямувала до нуля: , тобто кількість точок T- розбиття прямує до нескінченності (Зауважимо, що обернене не завжди справедливе). При такому T – розбитті границі виразів, що містяться в правій і лівій частині формули (1) прямуватимуть до площі криволінійної трапеції. Таким чином,

.

2. Такі задачі як визначення площі криволінійної трапеції, а також ряд інших, приводять до поняття визначеного інтегралу.

Нехай на деякому відрізку [a,b] задано функцію y=f(x). Проведемо T- розбиття відрізка [a,b] і побудуємо суму добутків значень функції в деяких точках відрізків T- розбиття помножених на довжини цих відрізків.

,

де x_i=x_i-x_i-1, i=1,2,…,n.

Означення. Якщо границя не залежить від виду T- розбиття, вибору точок на його відрізках і дорівнює сталому числу, то таке число називається визначеним інтегралом функції y=f(x) на відрізку [a,b].

Позначають

Тут f(x)- підінтегральна функція, f(x)dx –підінтегральний вираз, числа a,b – межі інтегрування.

Властивості визначеного інтегралу.

1. Якщо на відрізку [a,b] інтегрована функція f(x), то на цьому відрізку інтегрована і функція kf(x), причому

.

Доведення:

.

Аналогічно доводимо, що

2. Якщо на відрізку [a,b] функція f(x)=0, то .

3. Якщо на відрізку [a,b] функція f(x)=1, то .

4. Якщо на відрізку [a,b] функція f(x)0, то .

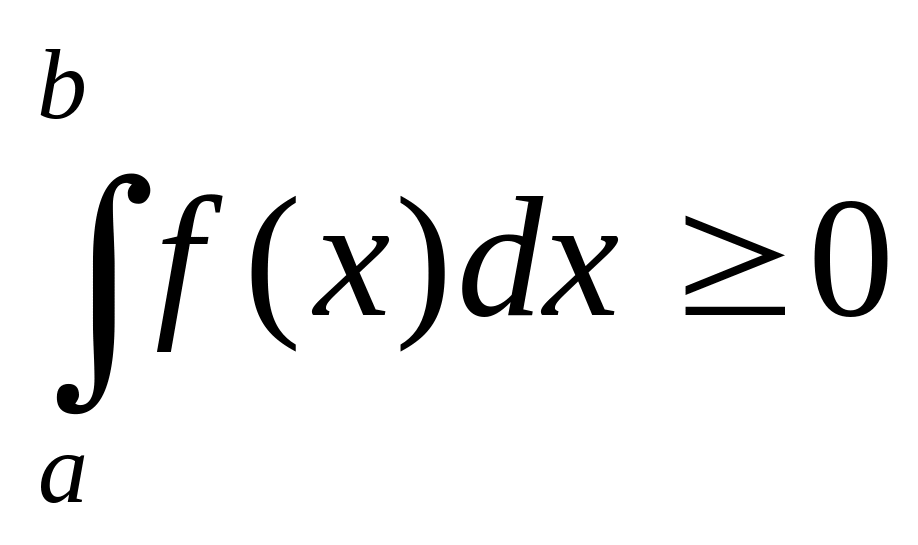5. Якщо на відрізку [a,b] інтегрована функція f(x), то на цьому відрізку інтегрована і функція , причому .

6. Якщо на відрізку [a,b] інтегровані функції f(x) та , то на цьому відрізку інтегровані і функції , причому (x)dx.

Без доведення приймемо твердження.

Теорема 1. Якщо функція інтегровна на відрізку [a,b], то вона обмежена на цьому відрізку.

Не всі функції, які ми розглядаємо є інтегровними, але можна виділити класи функцій, визначений інтеграл від яких існує.

Теорема 2. Якщо функція неперервна на відрізку [a,b], то вона інтегровна на цьому відрізку.

Теорема 3. Якщо функція монотонна на відрізку [a,b], то вона інтегровна на цьому відрізку.

Теорема 4. Якщо функція обмежена на відрізку [a,b] і неперервна в усіх точках цього відрізка, крім можливо, скінченної їх кількості, то вона інтегровна на цьому відрізку.

3. Теорема (про середнє). Якщо функція f(x) інтегровна на відрізку [a,b], то знайдеться така точка с[a,b], що .

Доведення. Так як функція f(x) інтегровна на відрізку [a,b], то вона обмежена на цьому відрізку, тобто існує таке значення M i m, що

.

З властивості 4 випливає, що якщо на відрізку [a,b] , то

.

Тобто

,

,

,

.

З останньої нерівності видно, що функція також обмежена, тобто існує така точка с[a,b], що f(c )= . А звідси очевидно

.

Теорему доведено.

Якщо функція f(x) інтегровна на відрізку [a,b], то поряд з інтегралом існує інтеграл . Можна говорити про деяку функцію F(x)= . Без доведення приймемо таке твердження:

Функція F(x)= є первісною для функції f(x).