Теоремы подобия, смещения, запаздывания
Теорема
подобия.
Дополнительное умножение аргумента
t
в оригинале на число а
R,
a
> 0 приводит в изображении к уменьшению
в а
раз параметра p
и самого изображения,
f(аt)
=:
F(
)
.
( 2 )
Доказательство.
f(аt)
=:
=
=
=
=
=
=
F(
)
Пр.6
sin at
=:
=
;
cosat
=:
=
Теорема смещения. Переход в изображении от p к (p + z), где z комплексное число, причем Re (p + z) > s0 , приводит к дополнительному умножению оригинала на экспоненту e-zt
F(p + z) =: e-zt f(t) ( 3 )
Доказательство.
e-zt
f(t)
=:
=
= F(p
+ z)
Пр.7
ezt
sin
at
=:
;ezt
cos at
=:
Теорема
запаздывания.
Уменьшение параметра t
в оригинале на величину
>
0 приводит к дополнительному умножению
изображения на экспоненту
f(t
-
)
=:
F(p)
( 4 )
Доказательство.
f(t
-
)
(t-
)
=:
F(p)
(t-
)
- функция Хевисайда (0 если t
<
,
1 еслиt
<
)
f(t
-
)
=:
=
+
+
Первый
интеграл равен 0, т.к.
(t-
)
= 0 при t
<
.
f(t
-
) =:
=
=
=
=
F(p)
Пр.8
(t
-
)
=:
и (t
– a)
(t
- а) =:
с учетом Пр. 5 .
Поиск изображения по графику оригинала
Пр.9 По данному графику оригинала найти изображение.
Построим аналитическое выражение для данной функции,
на основе общего уравнения прямой, проходящей через
две
точки (t1,
y1)
, (t2,
y2)
=
( 5 )
и
свойств единичной функции
(t
- а) =
(t)
(t)
-
(t
- а)
Решение.
Функцию на интервале [0 , a]
описывает разность двух единичных
функций
(t)
-
(t
- а) . Первую наклонную определим из ( 5
) по точкам (2а,
0), (а,
1): y
=-
(t
– 2a).
Для перехода от бесконечной прямой к
отрезку на интервале [a,
3a]
умножим уравнение на разность
(t
-а) -
(t
-3а)
Вторую наклонную определим из ( 5 ) по
точкам (4а,0)
, (3а,-1):
y
=
(t
– 4a),
и умножим уравнение на
(t
- 3а).
Сумма этих трех выражений определит
аналитический вид функции
f(t)
=
(t)
-
(t
- а) -
(t
– 2a)
[
(t
- а) -
(t
- 3а)]
+
(t
– 4a)
[
(t
- 3а)]
Представим
f(t)
в виде суммы слагаемых двух типов
(t
- b)
и (t
– b)
(t
- b)
f(t)
=
(t)
-
(t
- а) -
(t
– a)
(t
- а) +
(t
- а) +
(t
– 3a)
(t
- 3а)
+
(t
- 3а)+
+
(t
– 3a)
(t
- 3а)
-
(t
- 3а)
=
(t)
-
(t
– a)
(t
- а)
+
(t
–
3a)
(t
- 3а)
С помощью соотношений Пр.8 совершим переход к искомому изображению
F(t)
=:
-
+
.
Таблица изображений
-
№
f(t) при t>0
F(p)
№
f(t) при t>0
F(p)
1
1
9
t cos at
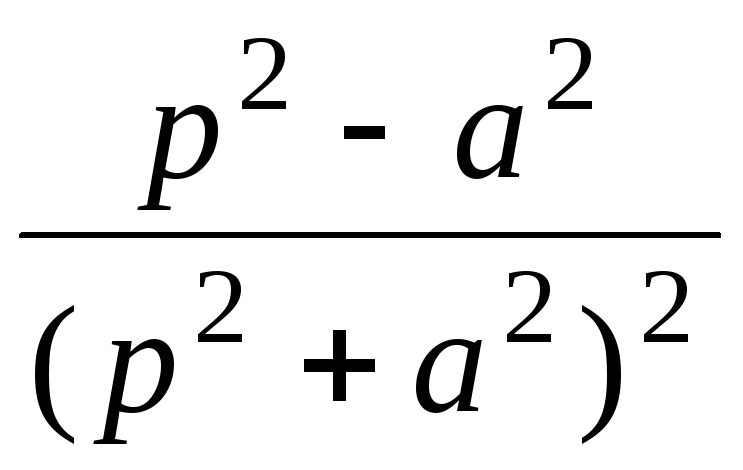
2
10
t sin at
3
eat
11
4
cos at
12
5
sin at
13
6
ezt cos at
14
7
ezt sin at
15
8
eat
16
