Лабораторная работа № 3 Резонансы напряжений и тока в электрических цепях

1. Цель работы.

Исследование явления резонанса в последовательном и параллельном контурах, их частотных характеристик, влияния нагрузки на свойства контуров.

2. Подготовка к выполнению работы.

При подготовке к работе необходимо изучить явления электрического резонанса в последовательном и параллельном контурах, основные расчетные соотношения, частотные характеристики контуров, влияние нагрузки на свойства контуров.

3. Последовательный контур.

3.1. Собрать схему последовательного колебательного контура (рис. 5)

подключенного к источнику Е.

_{Рис. 5}

_{3.2. Установить}

_{R = 20}

_Ом,

_{L = 2}

_мГн,

_{C = 50 + n ⋅ 5}

_{(нФ), где n – номер ла-}

бораторного макета.

_{3.3. Установить напряжение на выходе источника Е (или в точках 1 – 1¢),}

^{измеряемое по вольтметру, равным U} _вых

= 0,1 В.

3.4. Снять частотную характеристику

^U _L ^{= U} _вых ^{= f} ( ^f )

ненагруженного

_{последовательного контура в диапазоне частот, включающем в себя}

резонансную частоту

^f ₀ ^{, поддерживая напряжение на входе}

^U _вх ^на

каждой частоте постоянным и равным 0,1 В.

Для определения диапазона частот, в котором необходимо провести измерения, предварительно определите значение резонансной часто-

ты f ₀

по формуле:

₁

^{f 0 = .}

^{2p LC}

_{Остальные частоты можно получить, меняя частоту f в обе стороны от}

резонансной

^f ₀ ^{, например через 0,5 кГц.}

При измерении взять 5 точек ниже частоты резонанса и 5 точек

^{выше частоты резонанса (т.е. сдвиг 5 ⋅ 0,5 кГц = 2,5 кГц).}

^{Данные измерений записать в таблицу 6.}

_{Таблица 6}

Частота, кГц

f1

f 2

f 3

f 4

f 5

f 0

f 7

f 8

f 9

f10

f11

Rн =• (хх)

U L , В

Rн = 1 кОм

U L , В

_{По результатам измерений построить частотную характеристику (ре-}

зонансную кривую)

^U _L ^{= f ( f}

^{) , определить по ней полосу пропуска-}

ния

^S A ^{контура (на уровне 0,707U} L₀ ^{) и рассчитать значение доброт-}

_{ности ненагруженного контура:}

Q = f ₀

^S _A ^.

3.5. Снять частотную характеристику

U _L = U _вых = f ₍ f ₎

нагруженного

_{последовательного контура. Для этого подключить к выходу контура}

(к L ) сопротивление нагрузки R_н

_{сопротивления 1 кОм.}

(рис. 5), установив на нем значение

_{Проделать все измерения, построение графика и расчеты согласно}

^{п. 3.4. (Графики U} _L ^{= f ( f )}

для нагруженного и ненагруженного кон-

_{тура можно совместить). Данные измерений занести в таблицу 6. По}

^{результатам измерений и расчетов сделать вывод о влиянии R}_н

на из-

бирательные свойства последовательного контура, его эквивалентную добротность, полосу пропускания.

4. Параллельный контур.

4.1. Собрать схему параллельного колебательного контура, подключенно-

_{го к источнику J с большим внутренним сопротивлением (рис. 6) (у}

идеального источника тока

^R_вн ^{=• ).}

_{4.2. Установить}

_{L = 2}

_мГн,

_{R = 20}

_Ом,

_{C = 50 + n ⋅ 5}

_{(нФ). Установить ток}

_{генератора тока}

_{J = 10}

_мА.

^{4.3. Снять частотную характеристику ненагруженного ( R}_н

отключено)

параллельного контура

^U _к ^{= U} _вых ^{= f ( f )}

в диапазоне частот, вклю-

чающем в себя резонансную частоту

^f ₀ ^{, поддерживая ток генератора}

_{на каждой частоте постоянным и равным 10 мА. Расчет резонансной}

частоты

f ₀ сделать согласно формулы:

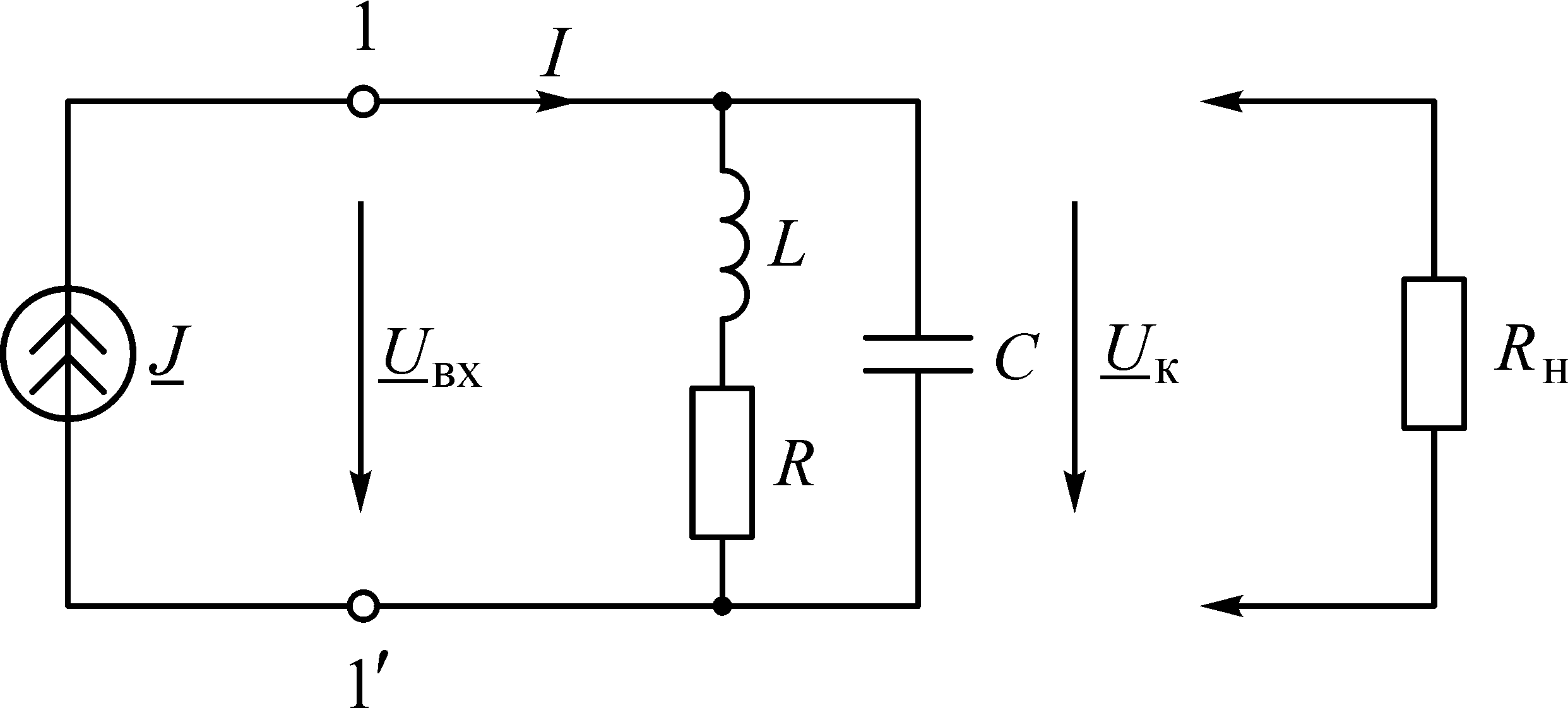
_{Рис. 6}

₁

^{f 0 =}

^{2p LC}

L C - R ²

^.

^{L C}

Остальные частоты так же, как в п. 3.4. Данные измерений записать в таблицу 7.

_{Таблица 7}

Частоты, кГц

f1

f 2

f 3

f 4

f 5

f 0

f 7

f 8

f 9

f10

f11

Rн =• (хх)

U к , В

Rн = 1 кОм

U к , В

_{По результатам измерений построить частотную характеристику (ре-}

зонансную кривую)

^U _к ^{= f ( f}

^{) , определить по ней полосу пропуска-}

ния

^S A ^{контура (на уровне 0,707U} к ₀ ^{) и рассчитать добротность Q не-}

нагруженного контура

_{Q = f 0}

^S _A ^.

4.4. Снять частотную характеристику

U _к = U _вых = f ₍ f ₎

нагруженного

контура. Для этого подключить к контуру сопротивление нагрузки

^{Rн =1 кОм (рис. 6).}

^{Проделать все измерения, построение графика и расчеты согласно}

_{п. 4.3. Данные измерений занести в таблицу 7.}

^{По результатам измерений и расчетов сделать вывод о влиянии R}_н ^на

эквивалентную добротность и полосу пропускания параллельного контура (т.е. на его избирательные свойства).

5. Требования к отчету.

Отчет должен содержать:

– схемы исследуемых цепей;

– данные элементов схемы;

– таблицы измеренных величин;

– графики частотных характеристик ненагруженного и нагруженно-

го последовательного и параллельного контуров;

– теоретический расчет добротностей и полос пропускания контуров

(по данным элементов схемы) – ненагруженного и нагруженного;

– выводы по работе, т.е. оценка влияния генератора и нагрузки на избирательные свойства контуров.