
- •116.1Теорема сложения вероятностей
- •116.2Свойства и статистический смысл дисперсии.
- •116.3Центральная предельная теорема Леви.
- •116.4Аксиоматика Колмогорова, вложение пред определений в аксиоматику.
- •705.1Возвратность цепей Маркова
- •705.2Условное мат ожидание и условное распределение одного подвектора норм случ вектора относит другого подвектора
- •705.3Многомерный нормальный вектор
- •705.4Свойства производящих функций, примеры их вычисления.
- •615.1Формула Байеса, примеры.
- •615.2Свойства производящих функций, примеры их вычисления.
- •615.3Случайные величины, их распределения, функции распределения и их свойства.
- •615.4Примеры использования производящих функций для вычисления моментов.
- •?.2 Математическое ожидание, механическая интерпретация, свойства.
- •?.4 Независимость событий, примеры независимых и зависимых событий.
- •??.2 Эргодическая теорема для цепей Маркова.
705.3Многомерный нормальный вектор
Многоме́рное норма́льное распределе́ние (или многоме́рное га́уссовское распределе́ние) в теории вероятностей— это обобщениеодномерного нормального распределения.
Случайный
вектор![]() имеет
многомерное нормальное распределение,
если выполняется одно из следующих
эквивалентных условий:
имеет
многомерное нормальное распределение,
если выполняется одно из следующих
эквивалентных условий:
1
Произвольная линейная
комбинациякомпонентов вектора![]() имеет
нормальное распределение или является
константой.
имеет
нормальное распределение или является
константой.
2
Существует вектор независимых
стандартных
нормальных случайных
величин
![]() ,
вещественный вектор
,
вещественный вектор![]() иматрицаА размерностиn*m,
такие что:
иматрицаА размерностиn*m,
такие что:
![]() .
.
3
Существует вектор
![]() инеотрицательно
определённаясимметричная матрица
инеотрицательно
определённаясимметричная матрица![]() размерностиn*n,
такие что плотность
вероятностивектораX
имеет вид:
размерностиn*n,
такие что плотность
вероятностивектораX
имеет вид:
![]()
где
![]() —
определитель матрицы
—
определитель матрицы![]() ,
а
,
а![]() —
матрицаобратнаяк
—
матрицаобратнаяк![]() .
.
4
Существует вектор
![]() и
неотрицательно определённая симметричная
матрица
и
неотрицательно определённая симметричная
матрица![]() размерностиn*n,
такие что характеристическая
функциявектораX
имеет вид:
размерностиn*n,
такие что характеристическая
функциявектораX
имеет вид:
![]()
замечания:
1Если одно из приведённых выше определений принято в качестве основного, то другие выводятся в качестве теорем.
2Вектор
![]() является
векторомсредних
значенийX,
а
является
векторомсредних
значенийX,
а
![]() —
егоковариационная
матрица.
—
егоковариационная
матрица.
3В случае n=1, многомерное нормальное распределение сводится к обычному нормальному распределению.
4Если
случайный вектор X
имеет многомерное нормальное распределение,
то пишут
![]() .
.
свойства многомерного распределения:
-Если
вектор
![]() имеет
многомерное нормальное распределение,
то его компоненты
имеет
многомерное нормальное распределение,
то его компоненты![]() имеют
одномерное нормальное распределение.
Обратное, вообще говоря, неверно!
имеют
одномерное нормальное распределение.
Обратное, вообще говоря, неверно!
-Если
случайные величины
![]() имеют
одномерное нормальное распределение
и совместнонезависимы,
то случайный вектор
имеют
одномерное нормальное распределение
и совместнонезависимы,
то случайный вектор![]() имеет
многомерное нормальное распределение.
Матрица ковариаций
имеет
многомерное нормальное распределение.
Матрица ковариаций![]() такого
вектора диагональна.
такого
вектора диагональна.
-Если
![]() имеет
многомерное нормальное распределение,
и его компоненты попарнонекоррелированы,
то они независимы. Однако, если только
компоненты
имеет
многомерное нормальное распределение,
и его компоненты попарнонекоррелированы,
то они независимы. Однако, если только
компоненты![]() имеют
одномерное нормальное распределение
и попарно не коррелируют, то отсюдане
следует, что они независимы.
имеют
одномерное нормальное распределение
и попарно не коррелируют, то отсюдане
следует, что они независимы.
Контрпример.
Пусть
![]() ,
а
,
а![]() с
равными вероятностями. Тогда если
с
равными вероятностями. Тогда если![]() ,
то корреляцияX
и Y
равна нулю. Однако, эти случайные величины
зависимы.
,
то корреляцияX
и Y
равна нулю. Однако, эти случайные величины
зависимы.
-Многомерное
нормальное распределение устойчивоотносительнолинейных
преобразований. Если![]() ,
а
A —
произвольная матрица размерности
m*n,
то
,
а
A —
произвольная матрица размерности
m*n,
то
![]() .
.
705.4Свойства производящих функций, примеры их вычисления.
Производящая функция
Производящая функция — способ задания вероятностных распределений. Используется чаще всего для вычисления моментов.
Пусть
есть случайная величина X
с распределением ![]() .
Тогда её производящей функцией моментов
называется функция, имеющая вид
.
Тогда её производящей функцией моментов
называется функция, имеющая вид
![]()
Пользуясь формулами для вычисления математического ожидания, определение производящей функции моментов можно переписать в виде:
![]()
то есть производящая функция моментов — это двустороннее преобразование Лапласа распределения случайной величины (с точностью до отражения).
Свойства производящих функций моментов
Свойства производящих функций моментов во многом аналогичны свойствам характеристических функций в силу похожести их определений.
Производящая функция моментов однозначно определяет распределение. Пусть X,Y суть две случайные величины, и
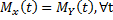 .
Тогда
.
Тогда  .
В частности, если обе величины абсолютно
непрерывны, то совпадение производящих
функций моментов влечёт совпадение
плотностей. Если обе случайные величины
дискретны, то совпадение производящих
функций моментов влечёт совпадение
функций вероятности.
.
В частности, если обе величины абсолютно
непрерывны, то совпадение производящих
функций моментов влечёт совпадение
плотностей. Если обе случайные величины
дискретны, то совпадение производящих
функций моментов влечёт совпадение
функций вероятности.Производящая функция моментов как функция случайной величины однородна:
![]()
Производящая функция моментов суммы независимых случайных величин равна произведению их производящих функций моментов. Пусть
 суть независимые случайные величины.
Обозначим
суть независимые случайные величины.
Обозначим  .
Тогда
.
Тогда
![]()
Пример: Производящая функция чисел Белла.
Альтернативный вариант ответа
Пусть
существует X-
случайная величина дискретного типа,
то есть принимает значения
![]() гдеX
целочисленное 0,1,2,…,k
с вероятностями p0,p1,…pk,
тогда производящей функцией мы называем
гдеX
целочисленное 0,1,2,…,k
с вероятностями p0,p1,…pk,
тогда производящей функцией мы называем
![]()
![]() ,
,
где Z- комплексная переменная, а X – случайная величина.
Свойства производящих функций:
1)
![]()
2)
![]()
![]()
3)Возьмем
![]() -
разложим в ряд Тейлора в точке (0).
-
разложим в ряд Тейлора в точке (0).![]() сравним (1) и (2)
сравним (1) и (2)![]() .
.
31//По производящей функции можно восстановить вероятности pk.
4)
![]()
Если
от
![]() в
(1) брать производные так как
в
(1) брать производные так как![]() при
при![]() можно брать любые производные.
можно брать любые производные.
![]() при
Z>1
тогда при Z=1
при
Z>1
тогда при Z=1
![]()
Необходимо, чтобы правая часть была конечна.
Частный случай:
![]()
![]()
5)
Если Y=aX+b
то
![]() (следует
из определения)
(следует
из определения)
6)
Если случайные величины X,Y
–независимы, то
![]()
![]() где
где
![]() независимы.
независимы.
Пример:
Вычислить производящую функцию распределения Пуассона.
Случайная величина принимает значения.
![]() где
k=0,1,2,…
где
k=0,1,2,…
тогда
![]()
где
![]()
Следствие:
Пусть
![]()
![]() -n
– независимых случайных величин, которые
имеют распределение Пуассона c
параметром
-n
– независимых случайных величин, которые
имеют распределение Пуассона c
параметром
![]() .
.![]() , тогдаY
тоже имеет распределение Пуассона с
параметром
, тогдаY
тоже имеет распределение Пуассона с
параметром
![]() .
.
Мы
получили
![]()
Пусть
 . Найти закон распределения, который
соответствует данной производящей
функции.
. Найти закон распределения, который
соответствует данной производящей
функции.
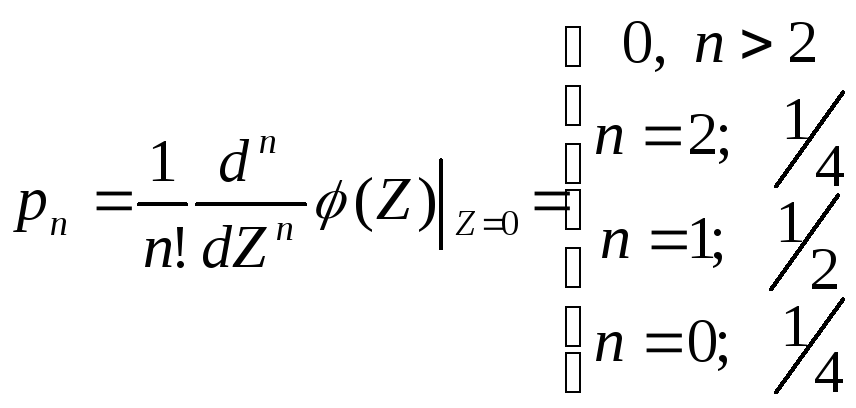 если
n>2;
то производная 0
если
n>2;
то производная 0
![]()
Случайная
величина принимает значение 0, 1, 2, с
вероятностями
![]()
Производящая функция называется производящей функцией момента (т.к. м. вычислить момент).
Вычислить
![]() для распределения Пуассона с параметром
для распределения Пуассона с параметром![]() .
.
![]()
Для распределения Пуассона получим формулу.
![]()
![]()
![]()
