4. Нагрузка от мостовых кранов

Расчетное усилие D_max ,передаваемое на колонну колесами крана определим по формуле:

D_max = γ_f · ψ · F_к · E_у + γ_f · G_n + γ_f · gⁿ · b_т ·b;

где γ_f – коэффициент надежности по нагрузке для крановых нагрузок, γ_f = 1,1;

ψ – коэффициент сочетаний при учете двух кранов, ψ = 0,85 – для весьма тяжелого режима;

F_к – нормативное вертикальное давление колеса, кН;

Е_у – сумма ординат линий влияния;

G_n – нормативный вес подкрановых конструкций, кН;

gⁿ – полезная нормативная нагрузка на тормозной площадке,

gⁿ = 1,5 кН/м²;

b_т – ширина тормозной площадки, м;

b – шаг колонн, м.

кН.

D_min = γ_f · ψ · F'_к · Е_у + γ_f · G_n + γ_f · gⁿ · b_т · b;

;

где Q – грузоподъемность крана, т;

Q_к – масса крана с тележкой, кН;

n – число колес с одной стороны крана.

кН.

кН.

Расчетная горизонтальная сила Т, передаваемая подкрановыми балками на колонну:

Т = γ_f · ψ · T_к · Е_у;

где Т_к – горизонтальная сила от мостовых кранов;

Е_у – сумма ординат линий влияния;

f = 0,05 – для кранов с гибким подвесом груза;

кН

Т = 1,1 · 0,85 · 30,4· 3,61 = 102,61064 кН

Расчетная схема рамы при действии крановых нагрузок на рис. 4.

Рис.4. Схема нагрузки от мостовых крано

3.3. Статический расчет поперечной рамы. Статический расчет рамы производится на ЭВМ. Таблица 1.

Таблица расчетных усилий в сечениях левой стойки рамы

(изгибающие моменты, кНм, нормальные и поперечные силы, кН)

4. Расчет внецентренно-сжатых колонн рам

1. Определение расчетных длин колонн в плоскости рамы

Расчетная длина колонны в плоскости рамы зависит от формы потери устойчивости и равна: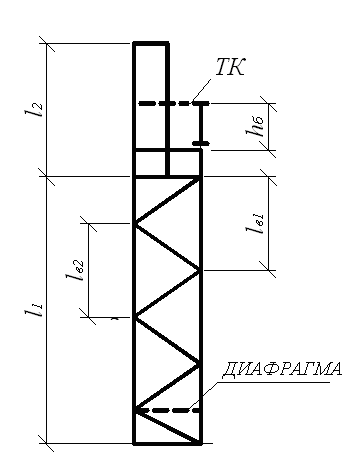

l_x = μ· l;

где μ – коэффициент приведения длины;

l – геометрическая длина стержня, м.

При Н_В/Н_Н = l₂/l₁ = 5770/8030 = 0,72 и N_H / N_B = 1682,55/287,55 = 5,85 > 3, значения μ₁ =2, μ₂ =3 – верхний конец колонны закреплен только от поворота.

Расчетная длина для нижней части колонны:

l_x1 = 2·1520 = 3040 см

Расчетная длина для верхней части колонны:

L_x2 = 3·640 = 1920 см

2. Определение расчетных длин колонн из плоскости рамы

Расчетная длина из плоскости рамы для нижней части колонны:

l_у1 = 1 1520=1520 см

Для верхней части колонны:

l_y2 = 0,8 640 = 512 см.

3. Расчет верхней части ступенчатой сплошной колонны

Сечение верхней части колонны принимаем в виде сварного двутавра высотой h_в = 700 мм.

Определим требуемую площадь сечения:

А_тр = N/ (φ_вн · R·γ),

где φ_вн – коэффициент снижения расчетного сопротивления при внецентренном сжатии, зависит от условной гибкости стержня λ_х и приведенного эксцентриситета m_x1;

γ – коэффициент условий работы, γ = 1.

,

где l_x2 – расчетная длина для верхней части колонны, см;

i_x – радиус инерции, см;

Е – модуль упругости, Е = 2,06·10⁴ кН/см².

Для симметричного двутавра:

i_x ≈ 0,42h; q_x = 2i_x²/ h ≈ 0,35h=24,5

где h – высота сечения колонны, см.

i_x = 0,42·70 = 29,4 см;

Приведенный эксцентриситет:

m_1x = η·m_x ,

где η – коэффициент влияния формы сечения;

m_x – относительный эксцентриситет.

m_x = e_x / q_x = M/ (N·0,35h),

m_x = 1283,34*100/ (957,6·24,5) = 5,5

Примем в первом приближении А_п / А_ст = 1, тогда

m_1x = 1,355 ·5,5 = 7,5

При λ_х = 2,25 и m_1x = 7,5 – φ_вн = 0,164

А_тр = 957,6/ 24,5*0,164 ≈ 238,3 см²

Компоновка сечения: высота стенки h_ст = h_в – 2t_п = 70 - 2·1,4 = 67,2 см, принимаем предварительно толщину полок t_п = 1,4 см.

При m >1 и λ >0,8 из условия местной устойчивости:

Принимаем t_ст = 1см.

Рис. 6.

Требуемая площадь полки:

см²

Назначаем конструктивно размеры полки не менее 200. Из условия устойчивости верхней части колонны из плоскости действия момента ширина полки:

b_п ≥ / t_f;

b_п ≥ 85.55/ 1.4 = 61.1=62 см.

Принимаем b_п = 62 см; t_п = 1,4 см.

Найдем геометрические характеристики сечения:

Полная площадь сечения:

А = 2·62·1,4 + 1·67,2 = 240.8 см²;

см⁴;

см;

см³;

Проверка устойчивости верхней части колонны в плоскости действия момента:

N/ φ_{x вн} ·А ≤ R·γ;

λ_x = 1920/ 29.12 = 66;

;

m_x = M_x *A/ (N·W_x) = 1283.34*100*240.8 / (957.6·5835.5) = 5.53;

η=1.4-0.02 =1.4-0.02*2.3=1.354

m_1x = η·m_x = 1.354·5.53 = 7.5

При λ_х = 2.3 и m_1x = 7.5 – φ_вн = 0,166

σ = 957.6/ (24.5*240.8*0.166) = 0.977 < 1