Граничные условия для векторов и .

Граничные условия для нормальных составляющих.

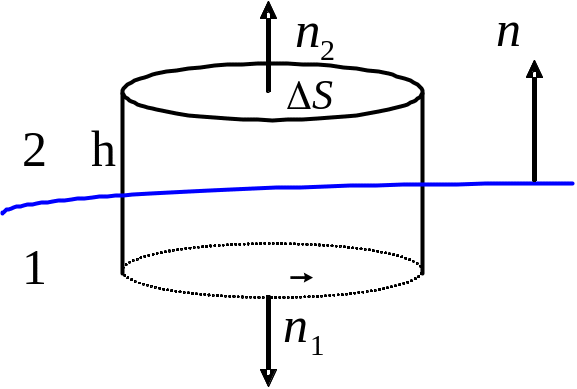
Рассмотрим границу раздела двух диэлектриков с диэлектрическими проницаемостями и (см. рисунок). Возьмем цилиндр очень малой

	высоты ( ), расположив его на границе раздела диэлектриков, как показано на рисунке, и воспользуемся теоремой Гаусса для вычисления потока вектора напряженности электрического поля через границу, разделяющую диэлектрики: ()

Сечение цилиндра должно быть выбрано таким, чтобы в пределах его торцов вектор всюду был одинаков. Тогда

.

Разные знаки составляющих потока вектора в выражении (4.2) обусловлены тем, что мы используем одну общую нормаль , направленную из первой среды 1 во вторую 2. Теперь устремим , при этом поток вектора , выходящий через боковую поверхность также устремится к нулю: . Тогда в пределе ( ) получаем

.

Итак:

Нормальная составляющая вектора напряженности электрического поля терпит разрыв на границе раздела двух диэлектриков.

Аналогично можно сосчитать поток векторов и через такую же цилиндрическую поверхность и получить граничные условия для них:

,

.

Однако, если на границе раздела диэлектриков нет сторонних зарядов ( ), то нормальная составляющая вектора электрической индукции непрерывна:

Граничные условия для тангенциальных составляющих.

Поместим небольшой прямоугольный контур вдоль границы раздела двух

диэлектриков, ориентировав его так, как показано на рисунке. Стороны контура, ориентированные вдоль границы раздела должны иметь такую длину , чтобы на её протяжении поле в каждом из диэлектриков не менялось, а «высота» контура должна быть пренебрежимо малой ( ). Воспользуемся теоремой о циркуляции для вектора :

В нашем случае:

.

Отсюда получаем

Вывод: Тангенциальные составляющие вектора напряженности электрического поля непрерывны (не меняются, не претерпевают скачка) при переходе через границу раздела диэлектриков.

Примеры вычисления полей в диэлектриках.

1). Точечный заряд в однородном и изотропном диэлектрике с диэлектрической проницаемостью .

Окружим заряд сферой радиуса и запишем теорему Гаусса для вектора электрической индукции:

Отсюда получаем выражения для электрической индукции и напряженности поля точечного заряда в веществе с известным значением диэлектрической проницаемости:

2). Диэлектрическая пластинка в однородном электрическом поле напряженностью .

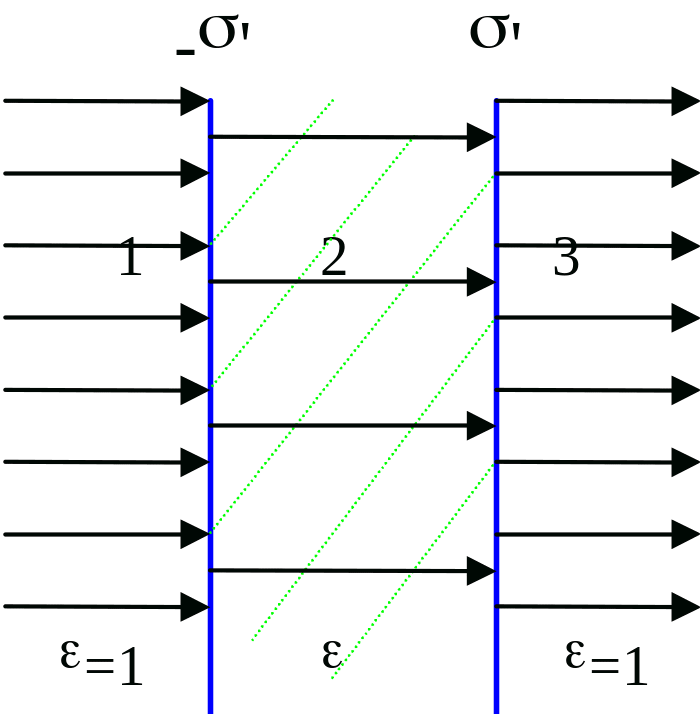
	Рассмотрим пластинку из диэлектрического материала, находящуюся в вакууме или в воздушной среде, диэлектрические проницаемости которых . Для простоты положим, что силовые линии поля перпендикулярны к поверхности пластины. На поверхности пластинки появляются связанные заряды, которые создают внутри пластины поле, направленное противоположно внешнему. Поскольку вектор

перпендикулярен поверхности пластинки (т.е. рассматривается только его нормальная составляющая) и сторонние заряды на пластинке отсутствуют ( ), то непрерывен во всех трех областях

Поле вне пластинки, например в области 1, совпадает с полем вектора электрической индукции:

Такое же поле в области 3. Поле внутри пластинки меньше поля снаружи (в вакууме) в раз:

Вектор поляризации также перпендикулярен пластинам и, учитывая, что , получаем из (4.5) и (4.9):

.

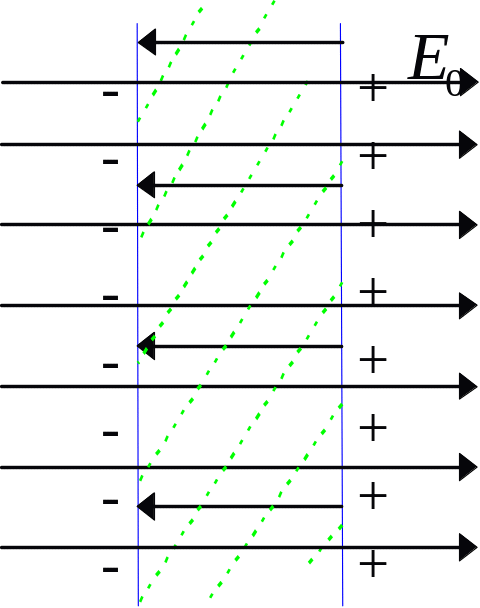
Примечание. Если пластинка находится между пластинами плоского конденсатора с плотностью стороннего заряда , то внешнее поле, создаваемое таким заряженным конденсатором, равно

.

Тогда получаем связь между плотностью сторонних зарядов и наведенных связанных зарядов:

На самом деле соотношение (4.22) справедливо для любого вида поверхности, разделяющей сторонние (в металле) и связанные (в диэлектрике) заряды.

Сегнетоэлектрики. Пьезоэффект.(СРС)