8. Независимость событий, примеры независимых и зависимых событий.

Вероятность появления события Апри условии, что событиеВпроизошло, называетсяусловной вероятностьюсобытияАи вычисляется по формуле:

где A, B E, P(B) 0.

События A, B Eназываютсянезависимыми, если.

В противном случае события АиВназываютсязависимыми.

Пример независимого события:

Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (событие A) равна 0,8, а вторым (событие В) — 0,7.

Решение.События А и В независимые, поэтому, по теореме умножения, искомая вероятность

Р(АВ) = Р(А)Р(В) = 0,7 * 0,8 = 0,56.

Пример зависимого события:

В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.

Решение.ОбозначимAизвлечение изношенного резца в первом случае, а— извлечение нового. Тогда. Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим.

Обозначим Bсобытие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:

Следовательно, вероятность события Bзависит от того, произошло или нет событиеA.

9. Формула полной вероятности, примеры.

Предположим, что в результате опыта может произойти одно из n несовместных событий (гипотез) Н₁,H₂,...,H_n. Пусть также имеется некоторое событие А и известны

Р(H_i) - вероятность гипотезы, P(A/H_i) - условная вероятность события А при этой гипотезе.

Тогда вероятность события А вычисляется по формуле полной вероятности:

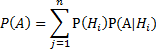
Доказательство. Заметим, что

и событияпопарно несовместны. Поэтому

Во втором равенстве мы использовали -аддитивность вероятностной меры, а в третьем — теорему умножения вероятностей.

Пример. Из 40 деталей 10 изготовлены в первом цехе, 25 - во втором, а остальные - в третьем. Первый и третий цехи дают продукцию отличного качества с вероятностью 0,9, второй цех - с вероятностью 0,7. Какова вероятность того, что взятая наудачу деталь будет отличного качества?

Решение: обозначим событие А = {выбрана деталь отличного качества},

H_i = {выбранная деталь изготовлена в i цехе}, i=1, 2, 3. Тогда

; ; .

По условию задачи

По формуле полной вероятности находим искомую вероятность:

10. Формула Байеса, примеры.

Формула Байеса

Пусть H₁,H₂,… — полная группа событий, и A — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие H_k, если в результате эксперимента наблюдалось событие A, может быть вычислена по формуле:

Доказательство. По определению условной вероятности,

Пример

Два стрелка подбрасывают монетку и выбирают, кто из них стреляет по мишени (одной пулей). Первый стрелок попадает по мишени с вероятностью 1, второй стрелок — с вероятностью 0,00001. Можно сделать два предположения об эксперименте:

H₁ = {стреляет 1-ый стрелок} и H₂ = {стреляет 2-ый стрелок}.

Априорные (a'priori — «до опыта») вероятности этих гипотез одинаковы:

Рассмотрим событие A = {пуля попала в мишень}. Известно, что

Поэтому вероятность пуле попасть в мишень

Предположим, что событие A произошло. Какова теперь апостериорная (a'posteriori — «после опыта») вероятность каждой из гипотез?

Очевидно, что первая из этих гипотез много вероятнее второй (а именно, в раз).

Действительно,