2. Дискретное вероятностное пространство, примеры.

Вероятностное пространство — это математическая модель случайного эксперимента (опыта) в аксиоматике А. Н. Колмогорова. Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, необходимую для его математического анализа средствами теории вероятностей. Любая задача теории вероятностей решается в рамках некоторого вероятностного пространства, полностью заданного изначально. Задачи, в которых вероятностное пространство задано не полностью, а недостающую информацию следует получить по результатам наблюдений, относятся к области математической статистики.

Дискретные вероятностные пространства.

Если множество элементарных исходов конечно или счетно: , то соответствующее вероятностное пространство называется дискретным. В случае дискретных вероятностных пространств событиями обычно считают все возможные подмножества . В этом случае для задания вероятности необходимо и достаточно приписать каждому элементарному исходу число так, чтобы их сумма была равна 1. Тогда вероятность любого события B задается следующим образом:

Важным частным случаем такого пространства является классический способ задания вероятностей, когда количество элементарных исходов конечно и все они имеют одинаковую вероятность. Тогда вероятность любого события определяется как отношение его мощности (т.е. количества элементарных исходов, благоприятствующих данному событию) к общему числу элементарных исходов:

Однако всегда необходимо помнить, что для того, чтобы применять данный способ, необходимо убедиться в том, что элементарные исходы действительно равновероятны. Это должно либо быть сформулировано как исходное условие, либо этот факт следует строго вывести из имеющихся начальных условий.

Пример. Монета бросается до первого появления герба. Доказать, что элементарному событию , состоящему в n бросаниях монеты, можно приписать вероятность . Найти вероятность того что:

1. Потребуется не менее двух бросаний;

2. Потребуется не четное количество бросаний.

3. Парадоксы доаксиоматической теории вероятностей.

Парадокс Бертрана.

При различных сопоставлениях событию А множества А' получается различный ответ в решении задачи.

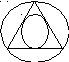
Задача. Имеется круг. В нем случайным образом выбирается хорда. Определить вероятность того, что длина хорды будет меньше длины стороны правильного треугольника, вписанного в этот круг.

4.Аксиоматика Колмогорова, вложение пред определений в аксиоматику.

Пусть F- некоторая система подмножеств множества элементарных событий Ω,F={A,B, …},ACΩ ,BCΩ, … МножествоFназывается алгеброй (σ-алгеброй), если выполнены следующие условия:

1. Ω € F

2. Если А € F, то Ā €F. (Ā – дополнительное событие к А, заключ. в том, что А не произошло)

3. Если А € FиB€F, то АUB€Fи А ∩B€F.

P- вероятностное распределение на σ-алгебре (алгебреF).P(A) – вероятность события А, где А €F. Выполнены следующие аксиомы:

1. P(Ω)=1

2. 0<=P(A)<=1.

3. Если A,B € F и A∩B=0, то P(AUB)=P(A)+P(B)

СуммаА+В (AUB) – называется такое событие, которое состоит в том, что либо произошло А, либо В, либо оба.

Из А следует В (А=> B) если событие А может произойти только с В.

Дополнение (отрицание)к событию А – Ā, называется событие, которое состоит в том, что А не произошло.

Разности событийА\В называется такое событие, которое состоит в том, что А произошло, а В не произошло.