30. Центральная предельная теорема Леви. Вывод из неё интегральной теоремы Муавра-Лапласа.
Теорема Леви
Теорема Леви в теории вероятностей — результат, увязывающий поточечную сходимость характеристических функций случайных величин со сходимостью этих случайных величин по распределению.
Формулировка:
Пусть 
последовательность случайных величин,
не обязательно определённых на одном
вероятностном
пространстве.
Обозначим характеристическую функцию
случайной величины Xn,
где 
,
символом φn(t).
Тогда если 
по распределению при 
,
и φ(t)
— характеристическая функция X,
то
Обратно, если 
,
где 
— функция действительного аргумента,
непрерывная
в нуле, то φ(t)
является характеристической функцией
некоторой случайной величины X,
и
Замечание:
Так как
характеристическая функция любой
случайной величины непрерывна в нуле,
второе утверждение имеет следующее
тривиальное следствие. Если 
,
где φn(t)
— характеристическая функция Xn,
и φ(t)
— характеристическая функция X,
то по распределению при 
.
Использование этого факта при
доказательстве сходимости по распределению
иногда называют методом
характеристических функций.
Метод характеристических функций
является стандартным способом
доказательства классической Центральной
предельной теоремы.
Вывод из неё интегральной теоремы Муавра-Лапласа
Пусть 0< p <1, тогда
для схемы Бернулли при 
для любых a и b справедлива формула
.
Отсюда, в частности, следует, что для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k1 и k2, можно использовать формулу
где , , - функция Лапласа.
Точность этой приближенной формулы растет с ростом n.
Если npq сравнительно невелико, то лучшее приближение дает формула
и для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k1 и k2, можно использовать формулу
, где , .
31. Свойства производящих функций, примеры их вычисления.
Производящая функция
Производящая функция — способ задания вероятностных распределений. Используется чаще всего для вычисления моментов.
Пусть есть случайная
величина X
с распределением 
.
Тогда её производящей функцией моментов
называется функция, имеющая вид
Пользуясь формулами для вычисления математического ожидания, определение производящей функции моментов можно переписать в виде:
то есть производящая функция моментов — это двустороннее преобразование Лапласа распределения случайной величины (с точностью до отражения).
Свойства производящих функций моментов
Свойства производящих функций моментов во многом аналогичны свойствам характеристических функций в силу похожести их определений.
Производящая функция моментов однозначно определяет распределение. Пусть X,Y суть две случайные величины, и
.
Тогда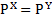 
.
В частности, если обе величины абсолютно
непрерывны, то совпадение производящих
функций моментов влечёт совпадение
плотностей. Если обе случайные величины
дискретны, то совпадение производящих
функций моментов влечёт совпадение
функций вероятности.Производящая функция моментов как функция случайной величины однородна:
Производящая функция моментов суммы независимых случайных величин равна произведению их производящих функций моментов. Пусть
суть независимые случайные величины.
Обозначим 
.
Тогда
Пример: Производящая функция чисел Белла.
Альтернативный вариант ответа
Пусть существует
X-
случайная величина дискретного типа,
то есть принимает значения
гдеX
целочисленное 0,1,2,…,k
с вероятностями p0,p1,…pk,
тогда производящей функцией мы называем
,
где Z- комплексная переменная, а X – случайная величина.
Свойства производящих функций:
1)
2)
3)Возьмем
-
разложим в ряд Тейлора в точке (0).
сравним (1) и (2)
.
31//По производящей функции можно восстановить вероятности pk.
4)
Если от
в
(1) брать производные так как
при
можно брать любые производные.
при Z>1
тогда при Z=1
Необходимо, чтобы правая часть была конечна.
Частный случай:
5) Если Y=aX+b
то
(следует
из определения)
6) Если случайные
величины X,Y
–независимы, то
где
независимы.
Пример:
Вычислить производящую функцию распределения Пуассона.
Случайная величина принимает значения.
где
k=0,1,2,…
тогда
где
Следствие:
Пусть
-n
– независимых случайных величин, которые
имеют распределение Пуассона c
параметром
.
, тогдаY
тоже имеет распределение Пуассона с
параметром
.
Мы получили
Пусть
. Найти закон распределения, который
соответствует данной производящей
функции.
если n>2;
то производная 0
Случайная величина
принимает значение 0, 1, 2, с вероятностями
Производящая функция называется производящей функцией момента (т.к. м. вычислить момент).
Вычислить
для распределения Пуассона с параметром
.
Для распределения Пуассона получим формулу.
