15. Свойства плотностей распределения.

Рассмотрим свойства плотности распределения f(x).

1. Всегда f(x)≥0, так как функция F(x) является неубывающей функцией.

2 Для функции распределения F(x) справедливо равенство:

Действительно, так как по определению f(x)=F'(x), то F(x) является первообразной функцией по отношению к плотности распределения f(x). Следовательно,

3. Вероятность попадания случайной величины в заданный интервал [Α ; Β] равна:

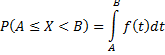
Действительно, в соответствии с формулой Ньютона-Лейбница этот определенный интеграл равен F(Β) - F(Α). По 3-му свойству функции распределения вероятностей эта разность и представляет собой вероятность P{Α≤X<Β} .

4. Интеграл от плотности распределения вероятности по всей области задания случайной величины равен единице:

Равенство представляет условие нормировки вероятностей для непрерывных случайных величин. По смыслу данный интеграл есть не что иное, как F(∞) = 1. Условие нормировки вероятностей часто используется для определения неизвестного параметра закона распределения.

Для иллюстрации геометрического смысла перечисленных свойств приведем пример графика плотности распределения вероятностей. Для большей наглядности на рис. представлен также график соответствующей функции распределения вероятностей.

Вся кривая плотности распределения вероятностей располагается выше оси OХ (свойство 1), причем максимум плотности достигается в точке х = а, в которой функция распределения вероятностей имеет наибольшую крутизну. Вероятность попадания случайной величины в интервал [Α ; Β] численно равна площади криволинейной трапеции, построенной на этом интервале как на основании и ограниченной сверху графиком плотности распределения (заштрихованная на рисунке область). Площадь всей криволинейной трапеции, заключенной между осью OХ и графиком плотности распределения, всегда равна единице. Любая функция, удовлетворяющая перечисленным выше свойствам, может быть плотностью распределения некоторой непрерывной случайной величины.

16. Математическое ожидание, механическая интерпретация, свойства.

Рассмотрим сначала следующий пример. Пусть на завод поступила партия, состоящая из N подшипников. При этом:

m₁ - число подшипников с внешним диаметром х₁,

m₂ - число подшипников с внешним диаметром х₂,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

m_n - число подшипников с внешним диаметром х_n,

Здесь m₁ + m₂ + ... + m_n = N. Найдем среднее арифметическое значение x_ср внешнего диаметра подшипника. Очевидно,

Внешний диаметр вынутого наудачу подшипника можно рассматривать как случайную величину , принимающую значения х₁, х₂, ..., х_n, c соответствующими вероятностями p₁=m₁/N, p₂=m₂/N, ..., p_n=m_n/N, так как вероятность p_i появления подшипника с внешним диаметром x_i равна m_i/N. Таким образом, среднее арифметическое значение x_ср внешнего диаметра подшипника можно определить с помощью соотношения

Пусть - дискретная случайная величина с заданным законом распределения вероятностей

Значения			…
Вероятности			…

Математическим ожиданием дискретной случайной величины называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е.

Возвращаясь к разобранному выше примеру, мы видим, что средний диаметр подшипника равен математическому ожиданию случайной величины - диаметру подшипника.

Математическим ожиданием непрерывной случайной величины с плотностью распределения называется число, определяемое равенством

При этом предполагается, что несобственный интеграл, стоящий в правой части равенства существует.

Рассмотрим свойства математического ожидания. При этом ограничимся доказательством только первых двух свойств, которое проведем для дискретных случайных величин.

1°. Математическое ожидание постоянной С равно этой постоянной.

Доказательство. Постоянную C можно рассматривать как случайную величину , которая может принимать только одно значение C c вероятностью равной единице. Поэтому .

2°. Постоянный множитель можно выносить за знак математического ожидания, т.е.

Доказательство. Имеем

3°. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин:

4°. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин: