5. Афинные преобразования

Определение. Аффинная система координат (или аффинным репером) на плоскости называется упорядоченная тройка точек этой плоскости не лежащих на одной прямой: R={О, Е1, Е2}.

Аффинное преобразование меняет и форму и размер.

Пусть на плоскости даны два аф-ых репера .

Возьмем произвольную координату изобразим точку , у которой в репере координаты такие же,как у точки в репере .

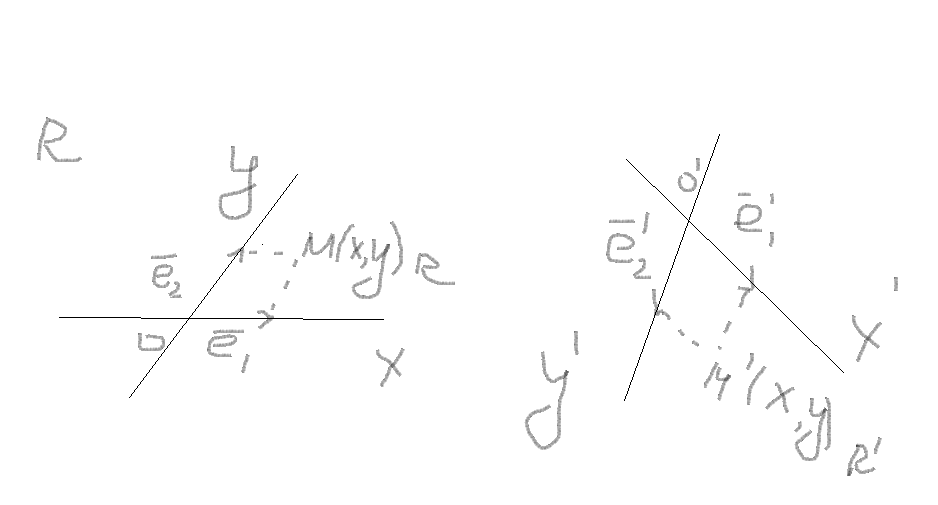
Преобразование плоскости,при каждая точка с координатами относительно репера отображается в точку с координатами относительно ,называется аффинным преобразованием плоскости.

Задается парой аффинных реперов.

Св-ва:

1.Множество аффинных преобразований плоскости образует группу.

2.каждая прямая при аффинном преобразовании переходит в прямую.

3.параллел прямые переходят в параллельные прямые

4.при аф.преобраз. сохраняется инцидентность точки и линии,если точка принадлежит линии, то образ точки лежит на образе линии.

5.Аф.преобраз. сохраняет отнош. Трех точек прямой

Если при аф преобр вектор , то вектор

Формулы аф.преобр.

Тот же рис что и выше

Определим репер в репере R

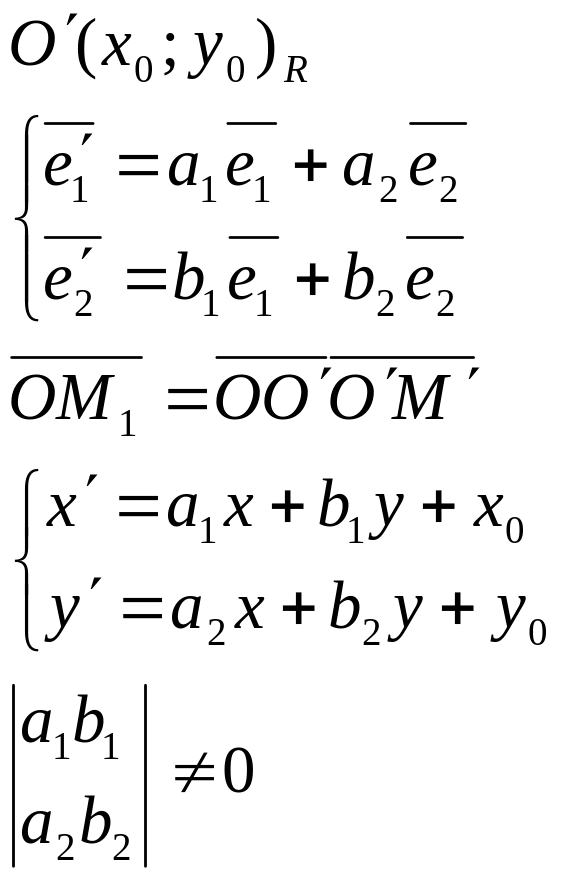
-формула аффинного преобразования

Верно иобратное,если преобраз задается данным формулами, то это аффинное преобраз.

Инвариантные точки.

Получим уравнение двух прямых.,если пр.пересек, то одна инвар. Точка, если прямые параллел-нет инвар. Точек,если прям совпад-бесчисл множество точек.

Т.Аф.преобр. плоскости либо не имеет инварианных точек либо имеет одну,либо бесконечное множество инвар.точек.Если аф. Преоб. Имеет прямую инвар.точек,то такое преобр назся проективно аффинным.а саму прямую называют осью родства или осью аффинитета.

аффинные преобразования образуют аффинную группу. В частности подгруппой аффинной группы преобразований является группа подобия (содержащая преобразования сдвига, поворота и изменения масштаба). В то же время аффинная группа является подгруппой общей линейной (проективной) группы, а евклидова группа является частным случаем аффинной группы преобразований.

Задача:

Часто бывает удобно при решении задач на аффинные свойства перейти с помощью аффинных преобразований к более простым фигурам, например, к правильному треугольнику. А затем с помощью обратного аффинного преобразования перенести полученный результат на искомую фигуру.

Для начала можно решить всем известную задачу о точке пересечения медиан треугольника.

Доказать, что медианы произвольного треугольника пересекаются в одной точке и делятся в отношении 2:1, считая от вершины.

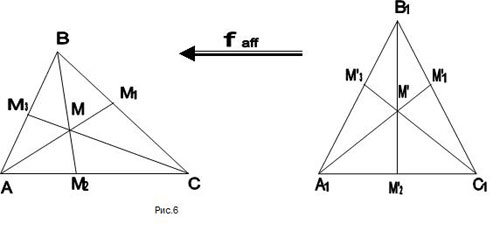
Решение (по алгоритму).

Пусть дан треугольник ABC. 1) Проверим аффинные свойства фигуры. Треугольник (по замечанию 1) является аффинной фигурой, быть медианой - это тоже аффинное свойство и отношения длин отрезков также сохраняется при аффинном отображении.

2) Значит, можно перейти к более удобной фигуре - равностороннему треугольнику.

3) Возьмем равносторонний треугольник . У этого треугольника медианы , пересекаются в одной точке (как высоты или биссектрисы равностороннего треугольника) и делятся этой точкой в отношении 2:1, считая от вершины. Действительно, и . А отношение из прямоугольного треугольника . Значит, .

4) Зададим аффинное отображение, переводящее треугольник в треугольник АВС. При этом отображении медианы треугольника переходят в медианы треугольника АВС и их точка пересечения переходит в точку пересечения их образов и она делит медианы произвольного треугольника ABC в отношении 2:1, считая от вершины.

5) Утверждение для произвольного треугольника доказано.