Вопрос 4.Определение преобразования плоскости.

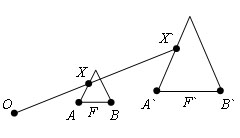
Если при преобразовании фигуры F в фигуру F` расстояние между точками изменяется в одно и тоже число раз, то такое преобразование называется преобразованием подобия. Т.е. произвольные точки AB фигуры F переходят в точки A`B` фигуры F`, так что A`B` =k*AB. Число k – это коэффициент подобия.

Движением называется отображение плоскости на себя при которром сохранаяются все расстояния между точками.

Гомотетией с центром в точке O и коэффициентом k называется такое отображение плоскости, при котором каждой точке X сопоставляется такая точка X', что OX' = kOX, причем не ислючается и возможность k<0.

Гомотетию с центром O и коэффициентом k часто обозначают через .

Свойства

-Если коэффициент гомотетии равен 1, то гомотетия является тождественным преобразованием: образ каждой точки совпадает с ней самой.

-Если коэффициент гомотетии равен -1, то гомотетия является центральной симметрией.

-Как и любое преобразование подобия, гомотетия преобразует прямую в прямую, отрезок в отрезок, луч в луч, угол в угол, окружность в окружность.

-Как и любое преобразование подобия, гомотетия сохраняет величины углов между кривыми.

- Анал.выр-е гомотетии

x’=kx+(k-1) x0 y’=ky+(k-1) y0

Т.Всякое преобразование подобия с коэфф.k можно представить в виде произведения гомотетии с тем же коэфф на движение.

Группа преобразований подобия и ее подгруппа

Существует хотя бы одна инвариантная точка

Т: мн-во всех преобразований подобия образует группу, наз.группой подобия

Подобие 1 рода образует группы: подгруппа группы преор.подобия.2 рода не образует.

Т.к. движение-частный случай преобр-я подобия. Основной инвариант:величина угла.отн-е подобия-отн-е эквив-сти. Эквив-е отн-я подобия являются подобными фигурами

Свойства подобия:

1. гомотет. c коэфф k есть преобразование подобия с коэфф |k|.

2. Всякое преобразование подобия с коэфф.k можно представить в виде произведения гомотетии с тем же коэфф на движение

Все свойства движения есть свойства подобия: отр в отр ,угол в угол, луч в луч, полуплоскость в полуплоскость. Доказанная теорема позволяет установить аналитический вид преобразования подобия

.Пусть начало координат точка О центр гомотетии. .

:

: -формула преобр подобия

И обратно: эти формулы задают преобразование подобия

Если k=1получаем формулы движения

Подобие 1р, 2р, в зависимости от того, движение какого рода определяет ее ориентацию. Т: всякое преобразование подобия отличное от движ-я им. 1 и только 1 инвариантную точку

Группы и подгр.

Пусть Н мно-во всех преобразований подобия.

Т1.Множество всех преобразований подобия образует группую

Основной инвариант величина угла.

Т2.мно-во подобий 1 рода образуют группу.Основ. инвариант ориентация угла.

Т3.Преобраз 2 рода группу не образуют.

Т4.Множество гомотетии с одним и тем же центром образует группу.

Т5.Всякая группа движений и ее подгр.явл.подгр.группы подобия.

Т6.Если гомотетия с разл. центрами присоединить совокупность параллельных переносов, то такая совокуп.образует группу.

Т: всякое преобразование подобия отличное от движ-я им. 1 и только 1 инвариантную точку

В некоторых задачах на построение данные бывают двух видов: одни определяют вид фигуры, которую нужно построить, другие – ее размеры. В этом случае удобно использовать метод подобия . Построение проводится поэтапно: сначала строят фигуру, подобную искомой, потом строят по заданным размерам саму искомую фигуру.

Рассмотрим применение метода на следующей задаче

Задача 2. В данный треугольник вписать квадрат так, чтобы две его вершины лежали на основании треугольника, а две других – на его боковых сторонах.

Решение. Пусть дан треугольник АВС. Нужно вписать в него квадрат.

Анализ. Предположим, что задача решена и искомый квадрат построен. Он подобен любому квадрату, у которого две вершины лежат на стороне АС, а третья – на стороне АВ. Построив такой квадрат и выполнив преобразование гомотетии, мы решим поставленную задачу.

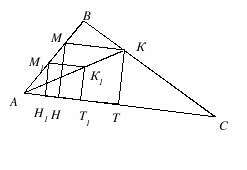
1. Строим произвольный квадрат Н1М1К1Т1, у которого две вершины лежат на стороне АС, а третья – на стороне АВ (пока не обращаем внимания на требование к четвертой вершине).

Из точки М1 опускаем перпендикуляр на АС, получаем отрезок М1Н1 – сторону квадрата.

На АС от точки Н1 отложим отрезок Н1Т1, равный М1Н1, получим вторую сторону квадрата.

Из точек М1 и Т1 проведем окружности радиусом М1Н1. На пересечении получим точку К1. Соединим точки, получим Н1М1К1Т1 – квадрат, у которого одна вершина не лежит на стороне треугольника.

2. Проведем луч АК1 до пересечения со стороной ВС, получим точку К.

3. Из точки К проведем прямую параллельно АС до пересечения с АВ, получим точку М.

4. Из точки К проведем прямую параллельно М1Н1 до пересечения с АС, получим точку Т; из точки М проведем прямую параллельно М1Н1 до пересечения с АС, получим точку Н.

5. Получили квадрат МКТН. Докажем, что квадрат МКТН – искомый.Доказательство.