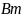- •Аннотация
- •Содержание
- •Введение
- •Глава I. Изоляционные конструкции
- •Вводы высокого напряжения
- •Электрический расчет ввода 132кВ с бми конденсаторного типа
- •Тепловой расчет ввода
- •Кабели высокого напряжения. Общие сведения.
- •1.2.1. Силовые кабели с поясной изоляцией
- •1.2.2. Электрический расчет кабеля.
- •Исходные данные:
- •1.2.3.Тепловой расчет кабеля.
- •1.3. Подвесные высоковольтные изоляторы
- •Стеклянные изоляторы
- •Фарфоровые изоляторы
- •Распределение напряжения вдоль гирлянды изоляторов
- •Расчет гирлянды напряжением 220кВ
- •Глава II. Потенциал ветроэнергетики в намибии
- •2.1. Демография Намибии
- •2.2. Ситуация энергетики в Намибии
- •2.4. Ветровая аккумулирующая электростанция
- •2.4.1. Описание изобретения
- •2.4.2.Принцип работы
- •2.4.3.Формула изобретения
- •Глава III. Меры безопасности при выполнении работ на электродвигателе
- •Заключение
- •Список используемой литературы
Тепловой расчет ввода
При проведении теплового расчета принимают тепловой поток вдоль оси изолятора равным нулю . из за небольшой поверхности стержня выступающего на воздухе, количество теплоты, отдаваемое внешним концом стержня в окружающую среду, невелико.
Зададимся
температурой
 . тепловыделение в токопроводящем
стержне длиной 1м.
. тепловыделение в токопроводящем
стержне длиной 1м.
 [1]
[1]
Здесь
 - удельное сопротивление меди
- удельное сопротивление меди
В первом считая от стержня , слое изоляции тепловыделение
 [1]
[1]
Где
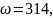
Зависимость
 от температуры для бумажно-масляной
изоляции (при частоте 50Гц ,
от температуры для бумажно-масляной
изоляции (при частоте 50Гц ,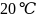
 )
приближенно выразим по формуле
)
приближенно выразим по формуле
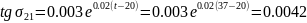 [3]
[3]
Находим перепад температур в первом слое изоляции.
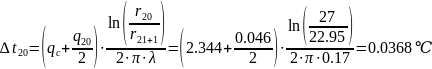 [1]
[1]
Где
 -
теплопроводность БМИ
-
теплопроводность БМИ
Перепад температур во втором слое

Где, –тепловыделение во втором слое
–тепловыделение во втором слое
 ,
,

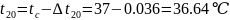
Аналогично рассчитываем перепады температур во всех слоях изоляции.
таблица 1.2.1
|
|||
|
|
|
|
I |
II |
III |
IV |
стержень |
2.344 |
37 |
3.218 |
20 |
0.046 |
36.64 |
0.061 |
19 |
0.043 |
36.633 |
0.054 |
18 |
0.041 |
36.679 |
0.050 |
17 |
0.040 |
36.714 |
0.046 |
16 |
0.039 |
36.741 |
0.044 |
15 |
0.039 |
36.763 |
0.042 |
14 |
0.040 |
36.781 |
0.040 |
13 |
0.041 |
36.796 |
0.039 |
12 |
0.042 |
36.808 |
0.038 |
11 |
0.044 |
36.819 |
0.038 |
10 |
0.047 |
36.828 |
0.038 |
9 |
0.051 |
36.836 |
0.038 |
8 |
0.055 |
36.843 |
0.039 |
7 |
0.061 |
36.848 |
0.040 |
6 |
0.068 |
36.853 |
0.041 |
5 |
0.078 |
36.857 |
0.043 |
4 |
0.09 |
36.860 |
0.045 |
3 |
0.107 |
36.862 |
0.048 |
2 |
0.132 |
36.863 |
0.052 |
1 |
0.167 |
36.863 |
0.057 |
сумма |
1.271 |
- |
0.893 |
Находим перепад температур в фарфоровой покрышке
 [1]
[1]
где
 -
теплопроводность фарфора
-
теплопроводность фарфора
перепад
температур от поверхности фарфоровой
покрышки в окружающую среду найдем при
вертикальном расположении изоляции.
Определяющий размер равен длине
воздушного конца изолятора
 .
Зададимся перепадом температур
.
Зададимся перепадом температур
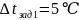 ,
тогда температура окружающей среды
будет
,
тогда температура окружающей среды
будет
 [1]
[1]
При
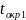 находим
:
находим
:
Коэффициент
кинематической вязкости воздуха,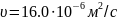
Коэффициент
теплопроводности воздуха, ,
число Прандтля
,
число Прандтля
 ,
,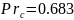 ; температурный коэффициент объемного
расширения воздуха,
; температурный коэффициент объемного
расширения воздуха,
 ;
;
Число
Грасгофа,
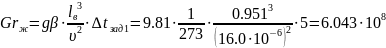
 [1]
[1]
При
вертикально расположенных трубах или
вертикальных плоских стенках средний
коэффициент теплоотдачи при
 определяется следующим образом;
определяется следующим образом;

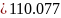 [1]
[1]
Находим коэффициент теплоотдачи при конвективном теплообмене.
 [1]
[1]
Перепад температур от стенки конструкции в окружающую среду
 [1]
[1]
Где S поверхность фарфоровой покрышки определим из формулы
 [1]
[1]
Полученный
перепад температур
 не равен
не равен
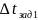 ,поэтому
расчёт повторяют, задавшись новым
значением перепада температур
,поэтому
расчёт повторяют, задавшись новым
значением перепада температур
 .Обычно
принимают
равным
.
.Обычно
принимают
равным
.
Зададимся
перепадом температур
 ,
тогда температура окружающей среды
будет
,
тогда температура окружающей среды
будет
 [1]
[1]
При
 найдем
:
найдем
:
Коэффициент
кинематической вязкости воздуха,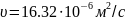
Коэффициент
теплопроводности воздуха,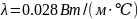 ,
число Прандтля
,
число Прандтля
 ,
, ; температурный коэффициент объемного
расширения воздуха,
;
; температурный коэффициент объемного
расширения воздуха,
;
Число Грасгофа,

 ,
то есть
,
то есть
При вертикально расположенных трубах или вертикальных плоских стенках средний коэффициент теплоотдачи при определяется следующим образом;
Находим коэффициент теплоотдачи при конвективном теплообмене.

Перепад температур от стенки конструкции в окружающую среду

Полученный
перепад температур
 не равен
,поэтому
расчёт повторяют ,задавшись новым
значением перепада температур
не равен
,поэтому
расчёт повторяют ,задавшись новым
значением перепада температур
 .Обычно
принимают
равным
.Проводят
изложенный выше расчет и определяют
.Обычно
принимают
равным
.Проводят
изложенный выше расчет и определяют
 ,который ,как правило не равен
.Расчет
следовало бы продолжить до тех пор ,пока
,который ,как правило не равен
.Расчет
следовало бы продолжить до тех пор ,пока
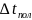 не станет равным
не станет равным
 .
Обычно это условие выполняется после
5-6 повторений расчета. С достаточной
для практики точностью определение
истинного перепада температур проще
выполнить графически.
.
Обычно это условие выполняется после
5-6 повторений расчета. С достаточной
для практики точностью определение
истинного перепада температур проще
выполнить графически.
Построив
зависимость
от
,
найдем (рис.3)
 , и тогда температура окружающей среды
составит:
, и тогда температура окружающей среды
составит:
 [1]
[1]

Рис.1.2.1. Определение перепада температур в окружающую среду.
Задаваясь температурами жил +60и -300С, проводим аналогичный расчет. Результаты расчета сведены в таблицу 1.2.2
Таблица 1.2.2
|
|
|
|
|
+60 |
59.855 |
0.16 |
2 |
57.6895 |
+37 |
36.863 |
0.15 |
1.88 |
34.833 |
-30 |
-30.114 |
0.121 |
1.57 |
-31.805 |
По
данным таблицы строим зависимость
суммарного перепада температур
 от температуры окружающей среды
от температуры окружающей среды



Рис.1.2.2 Зависимость суммарного перепада температур от стержня в окружающую среду от температуры окружающей среды



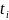 ,
,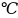
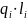 ,
,