13

Признаки объектов могут быть подразделены на детерминированные,

вероятностные, логические и структурные.

1. Детерминированные признаки – признаки, принимающие конкретные числовые значения (например, размах крыла , длина фюзеляжа , масса самолета G = 70 т и т.д.), которые могут рассматриваться в качестве координат точки в признаковом пространстве, соответствующей данному объекту. При рассмотрении признаков в качестве детерминированных ошибками измерений пренебрегают.

2. Вероятностные признаки – признаки, случайные значения которых распределены по всем классам объектов, при этом решение о принадлежности распознаваемого объекта к тому или другому классу может приниматься только на основании конкретных значений признаков данного объекта, определенных в результате проведения соответствующих опытов. Признаки распознаваемых объектов следует рассматривать как вероятностные и в случае, если измерение их числовых значений производится с такими ошибками, что по результатам измерений невозможно с полной определенностью сказать, какое числовое значение данная величина приняла.

3. Логические признаки распознаваемых объектов можно рассматривать как элементарные высказывания, принимающие два значения истинности («да», «нет» или «истина», «ложь») с полной определенностью. К логическим признакам относятся, прежде всего, признаки, не имеющие количественного выражения. Эти признаки представляют собой суждения качественного характера типа наличия или отсутствия некоторых свойств или некоторых элементов у распознаваемых объектов или явлений. В качестве логических признаков можно рассматривать, например, такие симптомы, используемые при медицинской диагностике, как боль в горле, кашель, насморк и т. д., такие свойства объектов геологической разведки, как растворимость или нерастворимость в определенных кислотах или в некоторых смесях кислот, наличие или отсутствие запаха, цвета и т. д. К логическим можно отнести также признаки, у которых важна не величина признака у распознаваемого объекта, а лишь факт попадания или непопадания ее в заданный интервал.

В пределах этих интервалов появление различных значений признаков у распознаваемых объектов предполагается равновероятным. На практике логические признаки подобного рода имеют место в таких ситуациях, когда либо ошибками измерений можно пренебречь, либо интервалы значений признаков выбраны таким образом, что ошибки измерений практически не оказывают влияния на достоверность принимаемых решений относительно попадания измеряемой величины в заданный интервал. Например, в области технической диагностики решение о выходе из строя технических устройств принимается лишь тогда, когда фактические значения некоторых параметров (признаков) превышают заданные интервалы. Отклонение же значений параметров от номинала, не сопровождающееся выходом за пределы соответствующих интервалов, является информацией о том, что устройство функционирует нормально.

4. Структурные (лингвистические, синтаксические) признаки представляют собой непроизводные элементы (символы) структуры объекта. Иначе эти элементы (константы) называют терминалами. Каждый объект может рассматриваться как цепочка терминалов или как предложение. Эти предложения и описывают объекты. При этом если предложение, описывающее неизвестный распознаваемый объект, относится к языку данного класса, то этот объект и принимается принадлежащим к этому классу. Например, при распознавании букв русского алфавита терминалами являются вертикальная, горизонтальная, наклонная черточка, наличие угла и т. д.

Классы объектов в соответствии с признаками:

Если признаки распознаваемых объектов – детерминированные, то описанием каждого класса объектов на языке этих признаков является его эталон, т.е. точка, сумма расстояний которой от точек, описывающих объекты, принадлежащие данному классу, минимальна.

Если признаки распознаваемых объектов – логические и имеют количественные выражения, то для описания классов объектов на языке признаков необходимо (в предположении достаточности исходной информации) определить диапазоны значений признаков , соответствующие классам При этом каждый из отрезков может рассматриваться как элементарное логической высказывание A, B, C,… . Если признаки распознаваемых объектов есть суждения качественного характера, то каждый из них также рассматривается как элементарное логическое высказывание . Для описания классов на языке этих признаков необходимо выяснить, какими из них характеризуется каждый класс, после этого установить зависимости в форме булевых соотношений между признаками A, B, C,…; и классами .

Если признаки распознаваемых объектов – структурные, то описаниями классов объектов являются языки, состоящие из предложений, каждое из которых характеризует структурные особенности объектов, принадлежащих исключительно одному из классов.

Выработка сведений о распознаваемых объектах и априорное описание классов – весьма трудоемкая часть в решении классификационных задач, требующая глубокого изучения свойств этих объектов.

Алгоритмы распознавания в соответствии с признаками:

Алгоритмы распознавания основываются на сравнении той или другой меры близости или меры сходства распознаваемого объекта с каждым классом. При этом, если выбранная мера близости L данного объекта с каким – либо классом превышает меру его близости с другими классами, то принимается решение о принадлежности этого объекта классу

В алгоритмах распознавания, базирующихся на использовании детерминированных признаков, в качестве меры близости используется среднеквадратичное расстояние между данным объектом и совокупностью объектов представляющих собой класс :

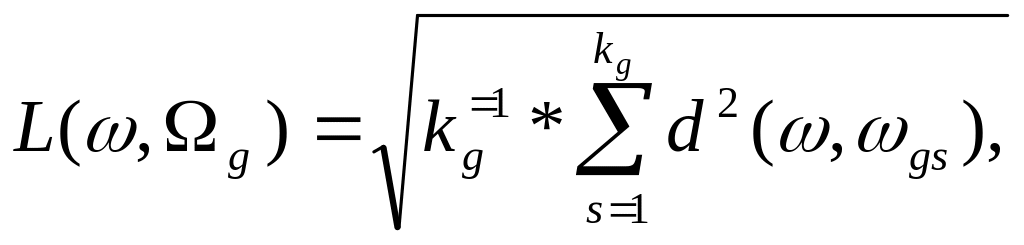
В алгоритмах распознавания, базирующихся на использовании вероятностных признаков, в качестве меры близости используется риск, связанный с решением о принадлежности распознаваемого объекта к классу

В алгоритмах распознавания, базирующихся на использовании логических признаков, не используется понятие «мера близости». Когда построено описание классов на языке логических признаков в виде соответствующих булевых соотношений (эквивалентности или импликаций), при подстановке в эти соотношения значений признаков, характеризующих распознаваемый объект, автоматически возникает ответ: к какому классу или классам этот объект может быть отнесен и к каким он не относится.

В алгоритмах распознавания, базирующихся на использовании структурных (лингвистических) признаков, понятие меры близости также не используется. Когда построены языки, описывающие классы в виде совокупностей предложений, характеризующих структурные особенности объекта, относящиеся к каждому классу, то распознавание неизвестного объекта осуществляется идентификацией предложения, описывающего этот объект, с одним из предложений языка – элемента описания соответствующего класса.

Искуственные нейронные сети биологический прототип

Нервная система человека, построенная из элементов, называемых нейронами, имеет ошеломляющую сложность. Около 10¹¹ нейронов участвуют в примерно 10¹⁵ передающих связях, имеющих длину метр и более. Каждый нейрон обладает многими качествами, общими с другими элементами тела, но его уникальной способностью является прием, обработка и передача электрохимических сигналов по нервным путям, которые образуют коммуникационную систему мозга.

Рис. 1.1. Биологический нейрон

На рис. 1.1 показана структура пары типичных биологических нейронов. Дендриты идут от тела нервной клетки к другим нейронам, где они принимают сигналы в точках соединения, называемых синапсами. Принятые синапсом входные сигналы подводятся к телу нейрона. Здесь они суммируются, причем одни входы стремятся возбудить нейрон, другие – воспрепятствовать его возбуждению. Когда суммарное возбуждение в теле нейрона превышает некоторый порог, нейрон возбуждается, посылая по аксону сигнал другим нейронам. У этой основной функциональной схемы много усложнений и исключений, тем не менее большинство искусственных нейронных сетей моделируют лишь эти простые свойства.

Искусственный нейрон

Искусственный нейрон имитирует в первом приближении свойства биологического нейрона. На вход искусственного нейрона поступает некоторое множество сигналов, каждый из которых является выходом другого нейрона. Каждый вход умножается на соответствующий вес, аналогичный синаптической силе, и все произведения суммируются, определяя уровень активации нейрона. На рис. 1.2 представлена модель, реализующая эту идею. Хотя сетевые парадигмы весьма разнообразны, в основе почти всех их лежит эта конфигурация. Здесь множество входных сигналов, обозначенных x₁, x₂,…,x_n, поступает на искусственный нейрон. Эти входные сигналы, в совокупности обозначаемые вектором X, соответствуют сигналам, приходящим в синапсы биологического нейрона. Каждый сигнал умножается на соответствующий вес w₁, w₂,…, w_n, и поступает на суммирующий блок, обозначенный Σ. Каждый вес соответствует «силе» одной биологической синаптической связи. (Множество весов в совокупности обозначается вектором W.) Суммирующий блок, соответствующий телу биологического элемента, складывает взвешенные входы алгебраически, создавая выход, который мы будем называть NET. В векторных обозначениях это может быть компактно записано следующим образом:

                                               NET = XW.

Рис. 1.2. Искусственный нейрон

Активационные функции

Сигнал NET далее, как правило, преобразуется активационной функцией F и дает выходной нейронный сигнал OUT. Активационная функция может быть обычной линейной функцией

                                               OUT = K(NET),

где К – постоянная, пороговой функции

                                               OUT = 1, если NET > T,                                                OUT = 0 в остальных случаях,

где Т – некоторая постоянная пороговая величина, или же функцией, более точно моделирующей нелинейную передаточную характеристику биологического нейрона и представляющей нейронной сети большие возможности.

Рис. 1.3. Искусственный нейрон с активационной функцией

На рис. 1.3 блок, обозначенный F, принимает сигнал NET и выдает сигнал OUT. Если блок F сужает диапазон изменения величины NET так, что при любых значениях NET значения OUT принадлежат некоторому конечному интервалу, то F называется «сжимающей» функцией. В качестве «сжимающей» функции часто используется логистическая или «сигмоидальная» (S-образная) функция, показанная на рис. 1.4а. Эта функция математически выражается как F(x) = 1/(1 + е^-x). Таким образом,

                                               .

По аналогии с электронными системами активационную функцию можно считать нелинейной усилительной характеристикой искусственного нейрона. Коэффициент усиления вычисляется как отношение приращения величины OUT к вызвавшему его небольшому приращению величины NET. Он выражается наклоном кривой при определенном уровне возбуждения и изменяется от малых значений при больших отрицательных возбуждениях (кривая почти горизонтальна) до максимального значения при нулевом возбуждении и снова уменьшается, когда возбуждение становится большим положительным. Гроссберг (1973) обнаружил, что подобная нелинейная характеристика решает поставленную им дилемму шумового насыщения. Каким образом одна и та же сеть может обрабатывать как слабые, так и сильные сигналы? Слабые сигналы нуждаются в большом сетевом усилении, чтобы дать пригодный к использованию выходной сигнал. Однако усилительные каскады с большими коэффициентами усиления могут привести к насыщению выхода шумами усилителей (случайными флуктуациями), которые присутствуют в любой физически реализованной сети. Сильные входные сигналы в свою очередь также будут приводить к насыщению усилительных каскадов, исключая возможность полезного использования выхода. Центральная область логистической функции, имеющая большой коэффициент усиления, решает проблему обработки слабых сигналов, в то время как области с падающим усилением на положительном и отрицательном концах подходят для больших возбуждений. Таким образом, нейрон функционирует с большим усилением в широком диапазоне уровня входного сигнала.

                                               .

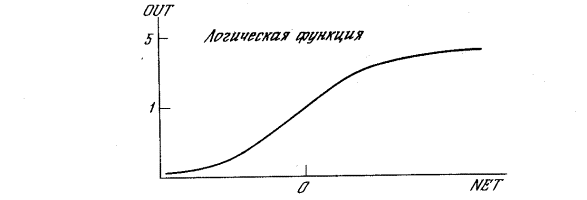
Рис. 1.4а. Сигмоидальная логистическая функция

Другой широко используемой активационной функцией является гиперболический тангенс. По форме она сходна с логистической функцией и часто используется биологами в качестве математической модели активации нервной клетки. В качестве активационной функции искусственной нейронной сети она записывается следующим образом:

                                               OUT = th(x).

Рис. 1.4б. Функция гиперболического тангенса

Подобно логистической функции гиперболический тангенс является S-образной функцией, но он симметричен относительно начала координат, и в точке NET = 0 значение выходного сигнала OUT равно нулю (см. рис. 1.4б). В отличие от логистической функции гиперболический тангенс принимает значения различных знаков, что оказывается выгодным для ряда сетей (см. гл. 3).

Рассмотренная простая модель искусственного нейрона игнорирует многие свойства своего биологического двойника. Например, она не принимает во внимание задержки во времени, которые воздействуют на динамику системы. Входные сигналы сразу же порождают выходной сигнал. И, что более важно, она не учитывает воздействий функции частотной модуляции или синхронизирующей функции биологического нейрона, которые ряд исследователей считают решающими.

Несмотря на эти ограничения, сети, построенные из этих нейронов, обнаруживают свойства, сильно напоминающие биологическую систему. Только время и исследования смогут ответить на вопрос, являются ли подобные совпадения случайными или следствием того, что в модели верно схвачены важнейшие черты биологического нейрона.