ПРИМЕРНАЯ БАЗА ТЕСТОВЫХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ «АНАЛИЗ ДАННЫХ И ПРОГНОЗИРОВАНИЕ ЭКОНОМИКИ» ДЛЯ СТУДЕНТОВ СПЕЦИАЛЬНОСТИ 050506-ЭКОНОМИКА
При моделировании экономических процессов встречаются с двумя типами данных:С) пространственные данные и временные ряды;
Примером пространственных данных являются:А) объемы производства в какой-то момент времени;
Исследованием экономических временных рядов с целью выделения бизнес-циклов (т.е. исследованием цикличности экономики) первым занялсяА) Жюгляр;
Для анализа или прогноза используются следующие основные классы моделей:Д) модели временных рядов, регрессионные модели с одним уравнением и системы одновременных уравнений;
К моделям временных рядов относятся следующие модели:Д) тренда, сезонности, тренда и сезонности;
Данные могут быть классифицированы как:
A) конечные и бесконечные;
B) дискретные и непрерывные;
C) дискретные и интервальные;
D) модальные и медианные;
E) целые и дробные.
**************************
7. Модой называют:
A) наблюдаемое значение признака;
B) варианту с наименьшей частотой;
C) варианту с наибольшей частотой;
D) варианту, приходящуюся на середину ранжированного вариационного ряда;
E) варианту, приходящуюся на первое или последнее место ранжированного вариационного ряда.
**************************
8. Медианой называют:
A) наблюдаемое значение признака;
B) варианту с наименьшей частотой;
C) варианту с наибольшей частотой;
D) варианту, приходящуюся на середину ранжированного вариационного ряда;
E) варианту, приходящуюся на первое или последнее место ранжированного вариационного ряда.
**************************
9. Какая характеристика ряда распределения находится по формуле:
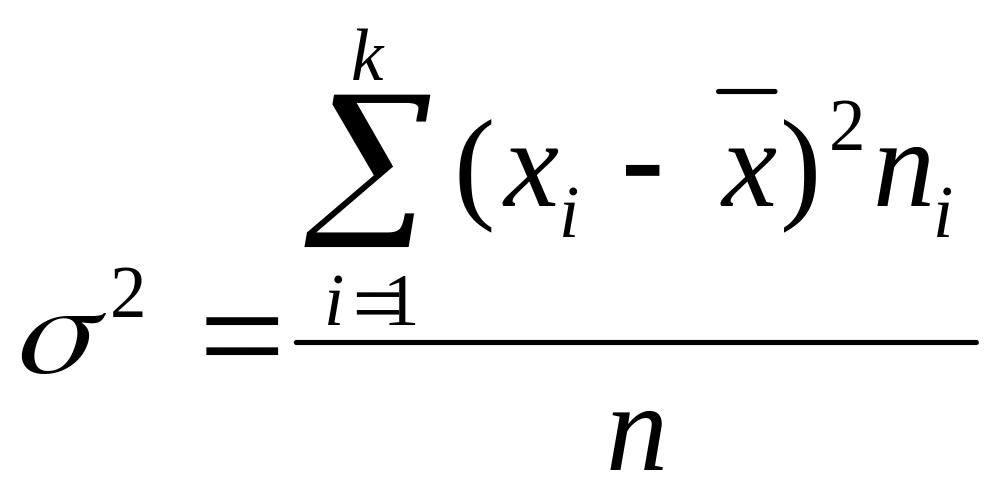
A) простая дисперсия;
B) взвешенная дисперсия;
C) обыкновенная дисперсия;
D) средняя арифметическая простая или взвешенная;
E) коэффициент вариации.
**************************
10. Какая характеристика ряда распределения находится по формуле:
A) простая дисперсия;
B) взвешенная дисперсия;
C) обыкновенная дисперсия;
D) средняя арифметическая простая или взвешенная;
E) коэффициент вариации.
**************************
11. Какая характеристика ряда распределения находится по формуле:
A) дисперсия;
B) среднее квадратическое отклонение;
C) средняя арифметическая;
D) среднее линейное отклонение;
E) коэффициент вариации.
**************************
12. Какая характеристика ряда распределения находится по формуле:
A) дисперсия;
B) среднее квадратическое отклонение;
C) средняя арифметическая;
D) среднее линейное отклонение;
E) коэффициент вариации.
**************************
13. Какая характеристика ряда распределения находится по формуле:
A) дисперсия;
B) среднее квадратическое отклонение;
C) средняя арифметическая;
D) среднее линейное отклонение;
E) коэффициент вариации.
**************************
14. Какая характеристика ряда распределения находится по формуле:
,
A) дисперсия;
B) среднее квадратическое отклонение;
C) средняя арифметическая;
D) среднее линейное отклонение;
E) коэффициент вариации.
**************************
15. Как изменится дисперсия, если варианты увеличить (или уменьшить) в одно и тоже число раз:
A) дисперсия увеличится (или уменьшится) на то же число;
B) дисперсия увеличится (или уменьшится) в квадрат этого числа;
C) дисперсия увеличится (или уменьшится) во столько же раз;
D) дисперсия не изменится;
E) дисперсия изменится на единицу.
**************************
16. Как изменится дисперсия, если варианты увеличить (или уменьшить) на одно и тоже число:
A) дисперсия увеличится (или уменьшится) на то же число;
B) дисперсия увеличится (или уменьшится) в квадрат этого числа;
C) дисперсия увеличится (или уменьшится) во столько же раз;
D) дисперсия не изменится;
E) дисперсия изменится на единицу.
**************************
17. Укажите формулу дисперсии:
A)
;
B)
;
C)
;
D)
;
E)
.
**************************
18. Какая характеристика ряда распределения находится по формуле:
?
A) ассоциации;
B) ассиметрии;
C) регрессии;
D) островершинности;
E) плосковершинности.
**************************
19. Какая характеристика ряда распределения находится по формуле
?
A) средняя степенная 5-го порядка;
B) начальный момент 5-го порядка;
C) средняя гармоническая 5-го порядка;
D) центральный момент 5-го порядка;
E) дисперсия в 5-ой степени.
**************************
20. Какой коэффициент из характеристик ряда распределения определяется по формуле:
?
A) коэффициент ассоциации;
B) коэффициент ассиметрии;
C) коэффициент регрессии;
D) коэффициент ассимиляции;
E) нет верных ответов.
**************************
21. Какой коэффициент
из характеристик ряда распределения
определяется по формуле:
?
A) коэффициент ассоциации;
B) коэффициент островершинности;
C) коэффициент регрессии;
D) коэффициент ассиметрии;
E) коэффициент регрессии.
**************************
22. Какая характеристика ряда распределения находится по формуле:
?
A) начальный момент 5-го порядка;
B) коэффициент ассиметрии;
C) коэффициент островершинности;
D) центральный момент 5-го порядка;
E) нет верных ответов.
**************************
23. Какая характеристика ряда распределения находится по формуле:
?
A) начальный момент 2-го порядка;
B) центральный момент 2-го порядка;
C) коэффициент ассиметрии;
D) коэффициент островершинности;
E) нет верных ответов.
**************************
24. Какой коэффициент
определяется по формуле:
?
A) коэффициент ассоциации;
B) коэффициент ассиметрии;
C) коэффициент регрессии;
D) коэффициент островершинности;
E) ) коэффициент детерминации.
**************************
25. Какой коэффициент
определяется по формуле:
?
A) коэффициент ассоциации;
B) коэффициент ассиметрии;
C) коэффициент регрессии;
D) коэффициент островершинности;
E) нет верных ответов.
**************************
26. О чем свидетельствует
данное выражение:
(эксцесс)>0
?
A) ряд несимметричный с правосторонней ассиметрией;
B) ряд симметричный;
C) распределение островершинное;
D) распределение плосковершинное;
E) распределение средневершинное, соответствующее нормальному.
**************************
27. О чем свидетельствует данное выражение: (эксцесс)<0 ?
A) ряд несимметричный с правосторонней ассиметрией;
B) ряд симметричный;
C) распределение островершинное;
D) распределение плосковершинное;
E) распределение средневершинное, соответствующее нормальному.
**************************
28. О чем свидетельствует данное выражение: (эксцесс)=0 ?
A) ряд несимметричный с правосторонней ассиметрией;
B) ряд симметричный;
C) распределение островершинное;
D) распределение плосковершинное;
E) распределение средневершинное, соответствующее нормальному.
**************************
29. О чем свидетельствует
данное выражение:
(коэффициент
ассиметрии)>0 ?
A) ряд несимметричный с правосторонней ассиметрией;
B) ряд симметричный;
C) ряд несимметричный с левосторонней ассиметрией;
D) распределение плосковершинное;
E) распределение средневершинное, соответствующее нормальному.
**************************
30. О чем свидетельствует данное выражение: (коэффициент ассиметрии)<0 ?
A) ряд несимметричный с правосторонней ассиметрией;
B) ряд симметричный;
C) ряд несимметричный с левосторонней ассиметрией;
D) распределение плосковершинное;
E) распределение средневершинное, соответствующее нормальному.
**************************
31. О чем свидетельствует данное выражение: (коэффициент ассиметрии)=0 ?
A) ряд несимметричный с правосторонней ассиметрией;
B) ряд симметричный;
C) ряд несимметричный с левосторонней ассиметрией;
D) распределение плосковершинное;
E) распределение средневершинное, соответствующее нормальному.
**************************
32. Какое свойство отражает (в математической форме) следующее выражение: ряд несимметричный с правосторонней ассиметрией ?
A) =0;
B) >0;
C) <0;
D) >0;
E) =0.
**************************
33. Какое свойство отражает (в математической форме) следующее выражение: ряд несимметричный с левосторонней ассиметрией ?
A) =0;
B) >0;
C) <0;
D) >0;
E) =0.
**************************
34. Какое свойство отражает (в математической форме) следующее выражение: ряд симметричный ?
A) =0;
B) >0;
C) <0;
D) >0;
E) =0.
**************************
35. Какое свойство отражает (в математической форме) следующее выражение: распределение островершинное ?
A) =0;
B) >0;
C) =0;
D) <0;
E) >0.
**************************
36. Какое свойство отражает (в математической форме) следующее выражение: распределение плосковершинное ?
A) =0;
B) >0;
C) =0;
D) <0;
E) >0.
**************************
37. Какое свойство отражает (в математической форме) следующее выражение: распределение средневершинное ?
A) =0;
B) >0;
C) =0;
D) <0;
E) >0.
**************************
38. Какой из центральных моментов используется для вычисления коэффициента ассиметрии ( )?
A) центральный момент 2-го порядка;
B) центральный момент 3-го порядка;
C) центральный момент 4-го порядка;
D) центральный момент 5-го порядка;
E) центральный момент 6-го порядка.
**************************
39. Какой из центральных моментов используется для вычисления коэффициента эксцесса ( )?
A) центральный момент 2-го порядка;
B) центральный момент 3-го порядка;
C) центральный момент 4-го порядка;
D) центральный момент 5-го порядка;
E) центральный момент 6-го порядка.
**************************
40. Чему равен
центральный момент порядка q
(
)
при q=0 (т.е.
)?
A) =1;
B) =0;
C)
=
;
D)
=
;
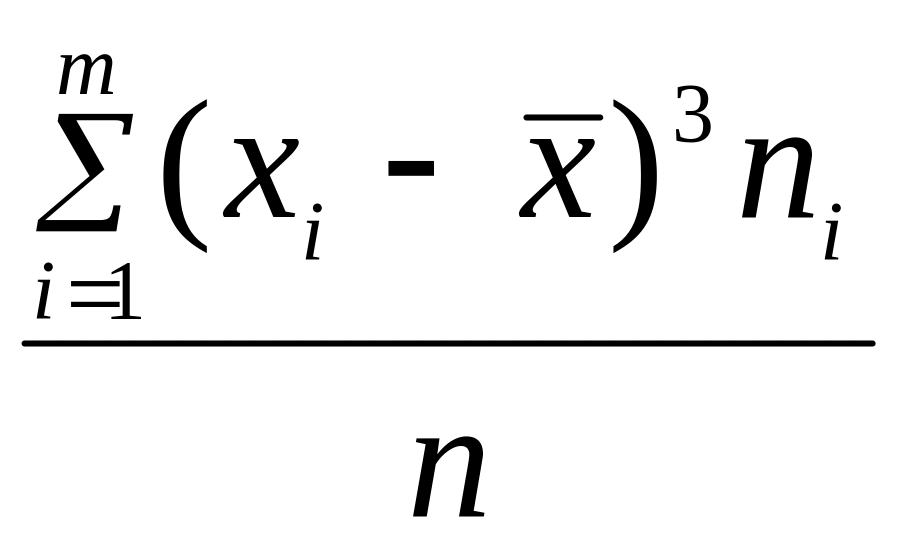E)
=
.
**************************
41. Чему равен
центральный момент порядка q
(
)
при q=1 (т.е.
)?
A) =1;
B) =0;
C) = ;
D) = ;
E) = .
**************************
42. Чему равен
центральный момент порядка q
(
)
при q=2 (т.е.
)?
A) =1;
B) =0;
C) = ;
D) = ;
E) = .
**************************
43. Чему равен
центральный момент порядка q
(
)
при q=3 (т.е.
)?
A) =1;
B) =0;
C) = ;
D) = ;
E) = .
**************************
44. Чему равен
центральный момент порядка q
(
)
при q=4 (т.е.
)?
A) =1;
B) =0;
C) = ;
D) = ;
E) = .
**************************
45. Чему равен
начальный момент порядка q
(
)
при q=0 (т.е.
)?
A) =1;
B)
=
;
C)
=
;
D)
=
;
E)
=
.
**************************
46. Чему равен
начальный момент порядка q
(
)
при q=1 (т.е.
)?
A) =1;
B) = ;
C) = ;
D) = ;
E) = .
**************************
47. Чему равен
начальный момент порядка q
(
)
при q=2 (т.е.
)?
A) =1;
B) = ;
C) = ;
D) = ;
E) = .
**************************
48. Чему равен
начальный момент порядка q
(
)
при q=3 (т.е.
)?
A) =1;
B) = ;
C) = ;
D) = ;
E) = .
**************************
49. Чему равен
начальный момент порядка q
(
)
при q=4 (т.е.
)?
A) =1;
B) = ;
C) = ;
D) = ;
E) = .
**************************
50. Какая величина является частным случаем начального момента порядка q ( ), q=1 ?
A) средняя арифметическая;
B) средняя квадратическая;
C) средняя степенная;
D) среднее квадратическое отклонение;
E) дисперсия.
**************************
51. Какая величина
является частным случаем центрального
момента порядка q (
),
q=2 ?
A) средняя арифметическая;
B) средняя квадратическая;
C) средняя степенная;
D) среднее квадратическое отклонение;
E) дисперсия.
**************************
52. Как обозначается уровень значимости ?
A)
;
B)
;
C)
;
D)
;
E)
.
**************************
53. Укажите формулу для расчета доверительного интервала:
A)
-
>а>+
;
B) - <а<+ ;
C)
-
<а<
+
;
D) - >а> + ;
E)
-
<а<
+
.
**************************
54. Точность оценки
(предельная ошибка)
=0,06,
=0,2.
Укажите доверительный интервал:
A) 0,2<p<0,26;
B) 0,012<p<0,3;
C) 0,06<p<0,2;
D) 0,14<p<0,26;
E) 0,14<p<0,2.
**************************
55. Предельная
ошибка выборочной доли составляет
=0,06,
выборочная доля
=0,2.
Укажите доверительный интервал:
A) 0,2<p<0,26;
B) 0,012<p<0,3;
C) 0,06<p<0,2;
D) 0,14<p<0,2.
E) 0,14<p<0,26;
**************************
56. Какие различают классы статистических гипотез ?
A) параметрические и непараметрические;
B) основные (нулевые) и альтернативные;
C) структурные и неструктурные;
D) основные и дополнительные;
E) главные и второстепенные.
**************************
57. Укажите классы статистических гипотез:
A) главные и второстепенные.
B) основные (нулевые) и альтернативные;
C) структурные и неструктурные;
D) основные и дополнительные;
E) параметрические и непараметрические;
**************************
58. На какие виды делятся все статистические гипотезы (параметрические и непараметрические) ?
A) главные и второстепенные.
B) нулевые и альтернативные;
C) структурные и неструктурные;
D) основные и дополнительные;
E) значимые и незначимые;
**************************
59. Что называют нулевой гипотезой ?
A) гипотезу, которая всегда противоречит основной;
B) если в ней сформулировано некоторое предположение относительно функции распределения случайной величины Х;
C) если в ней сформулированы предположения относительно параметра известного закона распределения случайной величины Х;
D) выдвинутую гипотезу;
E) главную гипотезу.
**************************
60. Что называют альтернативной гипотезой ?
A) гипотезу, которая всегда противоречит основной;
B) если в ней сформулировано некоторое предположение относительно функции распределения случайной величины Х;
C) если в ней сформулированы предположения относительно параметра известного закона распределения случайной величины Х;
D) выдвинутую гипотезу;
E) главную гипотезу.
**************************
61. Что называют непараметрической статистической гипотезой ?
A) гипотезу, которая всегда противоречит основной;
B) если в ней сформулировано некоторое предположение относительно функции распределения случайной величины Х;
C) если в ней сформулированы предположения относительно параметра известного закона распределения случайной величины Х;
D) выдвинутую гипотезу;
E) главную гипотезу.
**************************
62. Что называют параметрической статистической гипотезой ?
A) гипотезу, которая всегда противоречит основной;
B) если в ней сформулировано некоторое предположение относительно функции распределения случайной величины Х;
C) если в ней сформулированы предположения относительно параметра известного закона распределения случайной величины Х;
D) выдвинутую гипотезу;
E) главную гипотезу.
**************************
63. Как называется гипотеза, которая всегда противоречит основной ?
A) нулевая;
B) единичная;
C) альтернативная;
D) параметрическая;
E) непараметрическая.
**************************
64. Как называется выдвинутая гипотеза ?
A) нулевая;
B) единичная;
C) альтернативная;
D) параметрическая;
E) непараметрическая.
**************************
65. Как называется гипотеза, если в ней сформулированы предположения относительно параметра известного закона распределения случайной величины Х ?
A) нулевая;
B) единичная;
C) альтернативная;
D) параметрическая;
E) непараметрическая.
**************************
66. Как называется гипотеза, если в ней сформулировано некоторое предположение относительно функции распределения случайной величины Х ?
A) нулевая;
B) единичная;
C) альтернативная;
D) параметрическая;
E) непараметрическая.
**************************
67. Как называется гипотеза, если функция распределения задана однозначным образом ?
A) нулевая;
B) альтернативная;
C) простая;
D) сложная;
E) единичная.
**************************
68. Как называется гипотеза, если она состоит из конечного или бесконечного числа гипотез ?
A) нулевая;
B) альтернативная;
C) простая;
D) сложная;
E) единичная.
**************************
69. Как обозначается нулевая гипотеза ?
A)
;
B)
;
C)
;
D)
;
E) .
**************************
70. Как обозначается альтернативная гипотеза ?
A) ;
B) ;
C) ;
D) ;
E) .
**************************
71. Что называют ошибкой I рода ?
A) когда допускается ошибка в расчетах не более одного раза;
B) когда допускается ошибка в расчетах не более двух раз;
C) которая возникает, когда выдвигают гипотезу в первый раз;
D) когда отвергается правильная гипотеза;
E) когда принимается неправильная гипотеза.
**************************
72. Что называют ошибкой II рода ?
A) когда допускается ошибка в расчетах не более одного раза;
B) когда допускается ошибка в расчетах не более двух раз;
C) которая возникает, когда выдвигают гипотезу в первый раз;
D) когда отвергается правильная гипотеза;
E) когда принимается неправильная гипотеза.
**************************
73. Что называют статистической гипотезой ?
A) предположение (гипотезу), допустимое только в статистике;
B) гипотезу, в которой сформулировано некоторое предположение относительно функции распределения случайной величины Х;
C) гипотезу, в которой сформулированы предположения относительно параметра известного закона распределения случайной величины Х;
D) некоторое предположение относительно параметров случайной величины Х в генеральной совокупности или законов распределения этой случайной величины, которое необходимо проверить на основе данных выборки;
E) предположение о законе распределения величин.
**************************
74. Что называют областью принятия гипотезы ?
A)
область, определяемая неравенством
К>
;
B) область, определяемая неравенством К< ;
C)
область, определяемая неравенством
К<
,
К>
;
D) совокупность значения критерия, при которых нулевую гипотезу отвергают;
E) множество значений критерия, при которых нулевую гипотезу принимают.
**************************
75. Как называется совокупность значений критерия, при которых нулевую гипотезу отвергают ?
A) критическая область;
B) область принятия гипотезы;
C) правосторонняя критическая область;
D) левосторонняя критическая область;
E) двусторонняя критическая область.
**************************
76. Как называется множество значений критерия, при которых нулевую гипотезу принимают
A) критическая область;
B) область принятия гипотезы;
C) правосторонняя критическая область;
D) левосторонняя критическая область;
E) двусторонняя критическая область.
**************************
77. Что называют наблюдаемым значением ?
A) случайную величину К, с помощью которой принимают решение о принятии или отвержении нулевой гипотезы;
B) значения критерия, вычисленное по выборкам;
C) область, определяемая неравенством К< , К> ;
D) совокупность значения критерия, при которых нулевую гипотезу отвергают;
E) множество значений критерия, при которых нулевую гипотезу принимают.
**************************
78. Как называют случайную величину К, с помощью которой принимают решение о принятии или отвержении нулевой гипотезы ?
A) критической областью;
B) выборочным наблюдением;
C) наблюдаемым значением;
D) статистическим критерием;
E) областью принятия гипотезы.
**************************
79. В зависимости от количества факторов, включенных в уравнение регрессии различают:
А) однофакторную, двухфакторную регрессии;
В) простую (парную) и множественную регрессии;
С) простую (парную) и сложную регрессии;
Д) единственную и множественную регрессии;
Е) частную и общую.
**************************
80. Множественная регрессия соответственно представляет собой регрессию результативного признака с двумя и большим числом факторов, т.е. модель вида:
А)
f
В)
f
‘
С)
Д) log
Е)
f
.
**************************
81. Модель вида
f
представляет собой:
А) модель парной регрессии;
В) модель множественной регрессии;
С) динамическую модель;
Д) экономическую модель;
Е) функцию спроса.
**************************
82. Уравнение регрессии может включать следующее количество факторных признаков:
А) один и более;
В) два и более;
С) три и более;
Д) только один факторный признак;
Е) только два факторных признака.
**************************
83. Уравнение простой регрессии характеризует связь между:
А) двумя переменными (х и у);
В) тремя переменными
(
и
);
С) четырьмя
переменными (
и
);
Д) множеством
переменных (
и
);
Е) спросом и предложением.
**************************
84. Величина у (результативного признака) складывается из 2 слагаемых:
А)
(теоретическое значение результативного
признака) и х (факторного признака);
В) (теоретическое значение результативного признака) и М(х) (математического ожидания случайной величины);
С)
(теоретическое значение результативного
признака) и
(случайной величины, характеризующей
отклонение (у-
),
найденного по уравнению регрессии);
Д)
(теоретическое значение результативного
признака) и
(стандартной ошибки предсказываемого
значения по уравнению регрессии);
Е) спроса и предложения.
**************************
85. Случайная
величина
в модели
показывает:
А) величину теоретического значения ;
В) значение коэффициента регрессии;
С) показывает значение в точке пересечения линии регрессии с осью Оу;
Д) значение влияния неучтенных в модели факторов;
Е) разность а и b.
**************************
86 Свободный член а в модели показывает:
А) относительную
величину теоретического значения
;
В) абсолютную величину теоретического значения ;
С) показывает значение в точке пересечения линии регрессии с осью Оу;
Д) влияние неучтенных в модели факторов;
Е) разность и b.
**************************
87. Коэффициент b в модели показывает:
А) относительную величину теоретического значения ;
В) абсолютную величину теоретического значения ;
С) показывает значение в точке пересечения линии регрессии с осью Оу;
Д) влияние неучтенных в модели факторов;
Е) на сколько изменится значение результативного признака при изменении факторного на одну единицу.
**************************
88. Процесс построения уравнения регрессии включает следующие этапы:
А) выбор формулы уравнения регрессии;
В) определение параметров выбранного уравнения;
С) анализ качества уравнения и проверка адекватности уравнения;
Д) выбор формулы уравнения регрессии, определение параметров выбранного уравнения, анализ качества уравнения и проверка адекватности уравнения;
Е) нет правильных ответов.
**************************
89. Выбор вида математической функции может быть осуществлен:
А) графическим методом;
В) аналитическим методом;
С) экспериментальным методом;
Д) графическим методом, аналитическим методом, экспериментальным методом;
Е) методом группировок.
**************************
90. Уравнение
регрессии
графически представляется в виде:
А
)
В)
С)
Д) Е)
**************************
91. Уравнение
регрессии
графически представляется в виде:
А ) В) С)
Д) Е)
**************************
92. Уравнение
регрессии
графически представляется в виде:
А ) В) С)
Д) Е)
**************************
93. Уравнение
регрессии
графически представляется в виде:
А ) В) С)
Д) Е)
**************************
94.
Уравнение регрессии
графически представляется в виде:
А ) В) С)
Д) Е)
**************************
95. Число наблюдений, как показывают результаты исследований, должно превышать число рассчитываемых параметров при переменной х:
A) не менее, чем в 6-7 раз;
B) не менее, чем в 12-14 раз;
C) не менее, чем в 18-21 раз;
D) не менее, чем в 24-28 раз;
E) не менее, чем в 30-35 раз.
**************************
96. Оценка параметра а по методу наименьших квадратов из системы нормальных уравнений определяется по формуле:
A)
;
B)
;
C)
;
D) а= - b;
E) а= + b.
**************************
97. Оценка параметра b по методу наименьших квадратов из системы нормальных уравнений определяется по формуле:
A)
;
B)
;
C)
;
D)
;
E)
b=
а.
**************************
98. В уравнении регрессии параметр b называется:
A) свободным членом;
B) коэффициентом регрессии;
C) возмущением;
D) коэффициентом корреляции;
E) коэффициент детерминации.
**************************
99. Если коэффициент
регрессии (b) больше
0, т.е. b>0, то коэффициент
корреляции (
)
изменяется в следующих пределах:
A)
;
B)
;
C)
;
D)
;
E)
.
**************************
100. Одним из критериев оценки качества линейной модели служит:
A) свободный член а;
B) коэффициент регрессии b;
C) коэффициент детерминации;
D) средняя арифметическая;
E) дисперсия.
**************************
101.Оценка значимости уравнения регрессии, в целом, дается с помощью:
A) t - критерия Стьюдента;
B) F - критерия Фишера;
C)
- Пирсона;
D) формулы Стэрджеса;
E) формулы Фридмана.
**************************
102.Величина (
)
характеризует долю дисперсии у
вызванную:
A) ошибкой выбора формы связи;
B) ошибкой учтенных в модели факторов;
C) влиянием неучтенных в модели факторов;
D) влиянием всех (учтенных и неучтенных в модели факторов);
E) ошибкой выборки.
**************************
103. Расчету F-критерия Фишера для оценки значимости уравнения регрессии предшествует:
A) анализ дисперсии;
B) анализ корреляции;
C) анализ ковариации;
D) анализ характеристик ряда;
E) анализ группировок.
**************************
104. Какую информацию содержит ковариационно-корреляционная матрица?
A) выборочные ковариации между всеми возможными парами переменных;
B) выборочные линейные коэффициенты корреляции между всеми возможными парами переменных;
C) коэффициенты дисперсии между всеми возможными парами переменных;
D) выборочные ковариации между всеми возможными парами независимых переменных и линейные коэффициенты парной корреляции между факторными и результативным признаком;
E) дисперсии всех независимых переменных.
**************************
105. Какая форма связи множественной регрессии с 4-мя независимыми переменными, если она описывается функцией
?
A) линейная;
B) степенная;
C) экспоненциальная;
D) гиперболическая;
E) показательная.
**************************
106. Какая форма связи множественной регрессии с 4-мя независимыми переменными, если она описывается функцией
?
A) линейная;
B) степенная;
C) экспоненциальная;
D) гиперболическая;
E) показательная.
**************************
107. Какая форма связи множественной регрессии с 4-мя независимыми переменными, если она описывается функцией
?
A) линейная;
B) степенная;
C) экспоненциальная;
D) гиперболическая;