Производные обратных тригонометрических функций

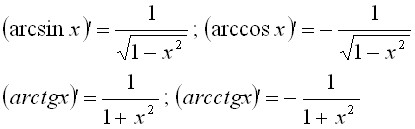
Основные формулы: 

Для сложных функций:

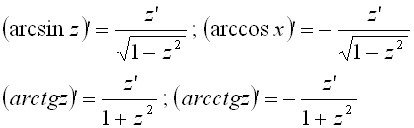
Рассмотрим обратные тригонометрические ф-ии.

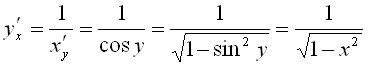
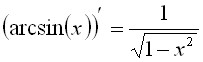
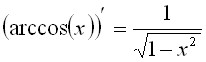
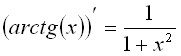
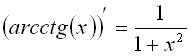
Производные от обратных тригонометрических функций

72. Неопределенные интегралы

      Пусть функция f(x), заданная в некотором промежутке^* [a, b], во всех его точках является производной функции F(x) , также заданной в [a, b]. Тогда эта последняя функция F(x) называется первообразной функцией для функции f(x) (в промежутке [a, b]).

     Имеет место

     Теорема 1. У всякой непрерывной на промежутке [a, b] функции имеется первообразная.

     Доказательство этой теоремы будет дано далее.

     Нетрудно видеть, что, если функция F(x) есть первообразная для f(x), то функция F(x) + C при любом постоянном C также является первообразной для f(x). В то же время никаких других первообразных, кроме функций вида F(x) + C, у f(x) уже быть не может. Действительно, еслиF₁(x) есть какая-то первообразная для f(x), то производная разности F₁(x) - F(x) будет всюду на [a, b] равняться нулю, а тогда сама разность есть величина постоянная, т. е.

F₁(x) - F(x) = C     и     F₁(x) = F(x) + C.

     Если F(x) есть первообразная функция для f(x), то функция двух аргументов x и C, равная F(x) + C, называется неопределенным интеграломфункции f(x) и обозначается символом

     Таким образом, неопределенный интеграл какой-нибудь функции представляет собой общий вид первообразных функций для этой функции. Величина C, входящая в определение неопределенного интеграла, называется "произвольной постоянной". Придавая ей то или иное закрепленное значение, можем получить из неопределенного интеграла любую первообразную.

     Легко понять, что из самого определения понятия интеграла вытекает следующее утверждение:

     Теорема 2. Производная неопределенного интеграла равна подинтегральной функции, т. е.