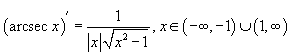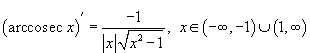Определение производной функции через предел

Пусть в некоторой окрестности точки   определена функция   Производной функции   в точке   называется предел, если он существует,

]Общепринятые обозначения производной функции в точке

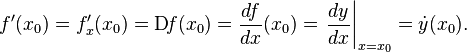
67. Геометрический смысл производной. Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

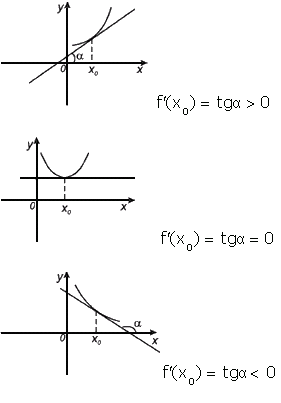
Рассмотрим график функции y = f ( x ):

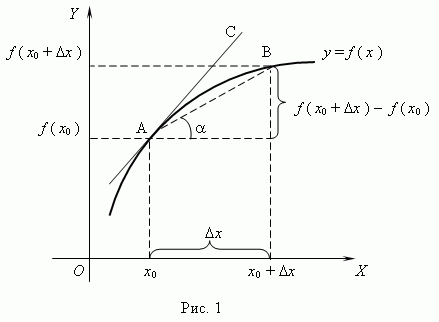
Из рис.1 видно, что для любых двух точек A и B графика функции:  xf(x0+ x)−f(x0)=tg , где   - угол наклона секущей AB.  Таким образом, разностное отношение равно угловому коэффициенту секущей.  Если зафиксировать точку A и двигать по направлению к ней точку B, то  x неограниченно уменьшается и приближается к 0, а секущая АВприближается к касательной АС.  Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует:

производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

В этом и состоит геометрический смысл производной.

68.Производная показательной и логарифмической функции

Предполагается, что основание a показательной и логарифмической функции больше нуля и не равно единице: a > 0, a ≠ 1. Производная показательной функции y = ax с основанием a определяется формулой

где ln a - натуральный логарифм a, т.е. логарифм a по основанию е, приблизительно равному 2,718281828... (2.7, затем два раза год рождения Л.Н.Толстого). Знаменитое трансцендентное число е можно вычислить с любой степенью точности с помощью различных компьютерных алгоритмов. Если a = е, то получаем красивый результат в виде

Производная логарифмической функции y = loga x определяется выражением

Для натурального логарифма y = ln x производная равна

69. вопрос РК 2, ответ 1,2

1. Производные тригонометрических функций

Производные шести тригонометрических функций и, соответственно, шести обратных тригонометрических функций определяются следующими формулами (рядом указана область определения каждой функции):

Пример 1

Вычислить производную функции  . Решение. Применим правило производной сложной функции несколько раз.        По формуле двойного угла        Следовательно, производная равна

2. Логарифмическая производная

Пример

Найти производную функции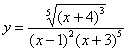 

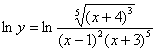
Собственно приступаем к дифференцированию.  Заключаем под штрих обе части:

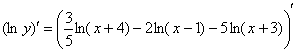
мы используем правило дифференцирования сложной функции  :

условие: 

Окончательный ответ:

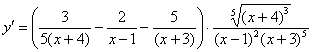
70. как 3 вопрос в РК 2

Таблица производных сложной функции

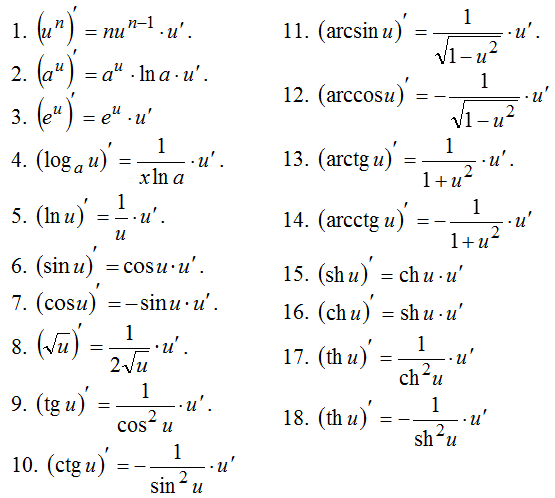
Сложная функция – это функция, аргументом которой также является функция.

С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать какf(g(x)). То есть, g(x) как бы аргумент функции f(g(x)).

К примеру, пусть f – функция арктангенса, а g(x) = lnx есть функция натурального логарифма, тогда сложная функция f(g(x)) представляет собой arctg(lnx). Еще пример: f – функция возведения в четвертую степень, а   - целая рациональная функция (смотритеклассификацию элементарных функций), тогда  .

В свою очередь, g(x) также может быть сложной функцией. Например, 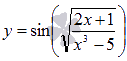 . Условно такое выражение можно обозначить как  . Здесь f – функция синуса,   - функция извлечения квадратного корня,   - дробная рациональная функция. Логично предположить, что степень вложенности функций может быть любым конечным натуральным числом  .

Часто можно слышать, что сложную функцию называют композицией функций.

Формула нахождения производной сложной функции.

Задание. Найти производную сложной функции 

Решение. Используем правила дифференцирования и таблицу производных сложных функций:

Ответ. 

71.

Пусть   - функция от аргумента x в некотором интервале  . Если в уравнении   y считать аргументом, а x - функцией, то возникает новая функция  , где   - функция обратная данной.