59. Способы задания функции

Различают 4 способа задания функции:

1. табличный Состоит в простом перечислении элементов функции f, т.е. при этом способе указывается значение аргумента x и соответствующе значение функции y=f(x)

x x1 x2 x3 x4

y y1 y2 y3 y4 Достоинства: точность, быстрота, по таблице значений легко найти нужное значение функции.

Недостатки: неполнота, отсутствие наглядности.

2. аналитический (формулы) Является наиболее важным для МА (мат.анализа), поскольку методы МА (дифференциального, интегрального счисления) предполагают этот способ задания. Одна и та же функция может быть задана различными формулами: y=∣sin(x)∣ y=√1−cos2(x) .

Часто при этом способе задания функции область определения не указывается, тогда под областью определения понимается естественная область определения, т.е. множество всех значений x при которых функция принимает действительное значение. Частным случаем аналитического способа задания функции является задание функции уравнением вида F(x,y)=0 (1) Если это уравнение обладает свойством, что ∀x∈ Д. Сопоставляется единственное y, такое, что

F(x,y)=0, то говорят, что уравнение (1) на Д неявно задает функцию. Еще один частный случай задания функции -- параметрический, при этом каждая пара (x,y)∈f задается с помощью пары функций

x=ϕ(t),y=ψ(t)

где t∈M .

3. графический Область определения -- проекция данного графика на Ох, а множество значений -- проекция Д(f) на Оу. Применяется в медицине, технике. Достоинство: наглядность.Недостаток: неточность.

4. словестный Отношение f, по которому каждому х находящееся соответствие у описывается словесно. Например, y=[x] : x из R (Целой частью х из R называют любое целое число не превосходящее х). Достоинство: можно воспользоваться когда первые три не срабатывают. Недостаток: ненаглядность

60. Предел функции. Определение. Свойства.

Предел функции. Число L называется пределом функции y = f ( x ) при x, стремящемся к a : если для любого > 0 найдётся такое положительное число = ( ), , зависящее от , что из условия | x - a | < , следует | f ( x ) – L | < . Это определение означает, что L есть предел функции y = f ( x ), если значение функции неограниченно приближается к L , когда значение аргумента x приближается к a.

lim

x → a (f(x) + g(x) - h(x)) =

lim

x → a f(x) +

lim

x → a g(x) -

lim

x → a h(x)

lim

x → a (f(x) * g(x)) =

lim

x → a f(x) *

lim

x → a g(x)

lim

x → a (cf(x)) = c *

lim

x → a f(x)

lim

x → a ( f(x)

g(x) ) = lim

x → a f(x)

lim

x → a g(x)

(

lim

x → a g(x) ≠ 0)

Число b называется пределом функции f(x) при x → a, если

для любого ε > 0 сущестувует δ > 0 такое, что для любого x

из δ-окрестности a (|x - a| < δ) выполняется |f(x) - f(a)| < ε.

Запись: ∀ ε > 0 ∃ δ > 0 : |x - a| < δ => |f(x) - f(a)| < ε

61. Бесконечно малые функции

Функция α(x), определенная в ·

O

(x 0), называется бесконечно малой функцией при x → x0, если lim

x → x0

α(x) = 0.

Свойства бесконечно малых функций

Пусть α(x) и β(x) — бесконечно малые функции при x → x0, и f(x) ограничена в некоторой проколотой окрестности точки x0. Тогда

1)α(x) + β(x) — бесконечно малая функция при x → x0;

2)α(x) · f(x) — бесконечно малая функция при x → x0.

Таблица эквивалентных бесконечно малых функций

При условии, что α(x) → 0 при x → x0 sin α(x) ~ α(x) 1 − cos α(x) ~ α(x)2

62. Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известныхматематических тождеств со взятием предела. Особенно известны:

• Первый замечательный предел:

• Второй замечательный предел:

63.

Свойства функций, непрерывных в точке

Поскольку точки   непрерывности функции   задаются условием  , то часть свойств функций, непрерывных в точке  , следует непосредственно из свойств пределов. Сформулируем их в виде следующей теоремы.

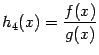        Теорема 3.1   Пусть функции   и   непрерывны в точке  . Тогда функции  ,  ,   непрерывны в точке  . Если  , то функция   также непрерывна в точке  .

        Доказательство.     Оно сразу же следует из теорем о пределах 2.8, 2.9, 2.10 и следствия 2.5.      

Как непосредственное следствие этой теоремы получается следующее

        Предложение 3.3   Рассмотрим множество всех функций, определённых в некоторой фиксированной окрестности   точки   и непрерывных в этой точке. Тогда это множество   является линейным пространством, то есть замкнуто относительно сложения и умножения на постоянные:

        Доказательство.     Действительно, постоянные   и   -- это непpеpывные функции (в любой точке); по пpедыдущейтеоpеме тогда непpеpывны в точке   пpоизведения   и  . Но тогда по этой же теоpеменепpеpывна в точке   и сумма  .      

        Теорема 3.2   Пусть функции   и   таковы, что существует композиция  ,  . Пусть функция   непрерывна в точке  , а функция  непрерывна в соответствующей точке  . Тогда композиция   непрерывна в точке  .

        Доказательство.     Заметим, что равенство   означает, что при   будет  . Значит,

(последнее равенство следует из непрерывности функции   в точке  ). Значит,

а это равенство означает, что композиция   непрерывна в точке  .      

Заметим, что, очевидно, в предыдущих двух теоремах можно было бы заменить базу   на односторонние базы   или   и получить аналогичные утверждения для непрерывности слева или справа:

        Теорема 3.3   Пусть функции   и   непрерывны слева (справа) в точке  . Тогда функции  ,  ,   непрерывны слева (соотв. справа) в точке  . Если  , то функция   также непрерывна слева (спpава) в точке  .    

        Теорема 3.4   Пусть функция   непрерывна слева (справа) в точке  , а функция   непрерывна в точке  . Тогда композиция   непрерывна слева (соотв. справа) в точке  .   

64.

операции над непрерывными функциями.

Теорема 1. Если функции f1(x) и f2(x) непрерывны в точке x0, то их сумма и произведение также непрерывны в точке x0. Если, кроме того, f2(x0) 0, то частное  также непрерывно в точке x0.

Доказательство. Доказательство основано на свойствах пределов. Докажем, например, что сумма непрерывных функций непрерывна. Функции f1(x), f2(x) непрерывны в точке x0, поэтому  f1(x) = f1(x0),  f2(x) = f2(x0). Применяя теорему о пределе суммы двух функций, получим:

(f1(x) + f2(x)) =  f1(x) +  f2(x) = f1(x0) + f2(x0),

что означает непрерывность f1(x) + f2(x) в точке x0. Аналогично для других утверждений теоремы. Заметим, что формулу f(x) = f(x0) (определяющую непрерывность функции f(x) в точке x0) можно записать в виде:  f(x) = f( x), так как  x = x0. Эта формула означает, что при нахождении предела непрерывной функции можно переходить к пределу под знаком функции.

Теорема 2. Если функция u = (x) непрерывна в точке x0, а функция y = f(u) непрерывна в точке u0 = (x0), то сложная функция y = f((x)) непрерывна в точке x0.

Доказательство. Покажем, что  f((x)) = f((x0)). Действительно, из непрерывности функции (x) имеем:  (x) = (x0) = u0, т.е. при x x0 следует, что u u0. Далее, из непрерывности функции f(u) получаем:

f((x)) =  f(u) = f(u0) = f((x0)).

Теорема доказана.

Установим непрерывность некоторых элементарных функций:

1. Всякая постоянная функция y = C непрерывна в каждой точке x0R, так как  C = C.

2. Функция y = x непрерывна в любой точке x0, так как  x = x0. Тогда функция  y = Cxn, где n N, непрерывна на всей числовой оси, как произведение непрерывных функций.

3. Любой многочлен: y = a0 + a1x + a2x2 + ...+ anxn, непрерывен в каждой точке числовой оси, как сумма непрерывных функций.

4. Всякая рациональная дробь, являющаяся отношением двух многочленов  , непрерывна во всех точках, в которых многочлен Q(x) не обращается в 0.

5. Функция y = sinx, y = cosxнепрерывны в точке x0 = 0, так как

sinx = 0, sin0 = 0,   cosx = 1, cos0 = 1, т.е.  sinx = sin0 и  cosx = cos0

(Это было доказано в разд. 1.9 ).

Сформулируем без доказательств следующую теорему.

Теорема 3. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.

Если функция f(x) непрерывна в каждой точке интервала (a, b), то говорят, что f(x) непрерывна на интервале (a, b). 

Пример 6. Функция f(x) =   непрерывна на интервалах (–, 3) и (3, +), так как при x0 3:  f(x) =   = f(x0).

65. Разрывность — Функция f(x) непрерывна при х = а, если при приближении х к а предел функции f(x) равен f(a); в этом случае lim f(х) = f(lim х). Если же это равенство не оправдывается, то говорят, что функция f(x) претерпевает разрыв при x=а.

Р. может появиться в следующих случаях: 1) если limf(x) не существует; 2) если limf(x) существует, но функция f(x) не имеет смысла при x = а; 3) если limf(x) и f(a) существуют, но limf(x) не = f(а).

66.Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование

Пусть в некоторой окрестности точки   определена функция   Производной функции называется такое число  , что функцию в окрестности  можно представить в виде

если   существует.