45. Общие уравнения прямой в пространстве

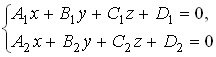
46. Каноническое уравнение плоскости в пространстве:

Аx+By+Cz+D=0, где D = -Ax0-By0-Cz0.

Параметрические уравнения прямой в пространстве:

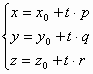
47. Угол между двумя плоскостями.

Пусть прямые l1 и l2 заданы уравнениями:

l1: y=k1x+в1

l2: y=k2x+в2

c углами наклона к оси Ох соответственно φ1 и φ2

Обозначим через φ1 угол наклона прямой l1 к оси Ох и через φ угол, на который нужно повернуть прямую l1 до совпадения с l2 (рис. 6).

Тогда φ1+φ=φ2 будет, очевидно, углом наклона прямой l2 к оси Oх. Отсюда φ=φ2-φ1 и если прямые l1 и l2 не являются перпендикулярными, то (по известной формуле тригонометрии)

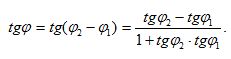
Заметив, что tgφ1=k1 и tgφ2=k2 получим:

Условия параллельности двух прямых:

а) Если прямые заданы уравнениями с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k1 = k2

б) Для случая, когда прямые заданы уравнениями в общем виде , необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

48. Ах2 + 2Вху + Су2 + 2Dx + 2Ey + F = 0. или

49. Эллипс и его параметры. Эллипс - это геометрическая фигура, которая ограничена кривой, заданной уравнением

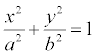
Он имеет два фокуса. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

Чертеж фигуры эллипс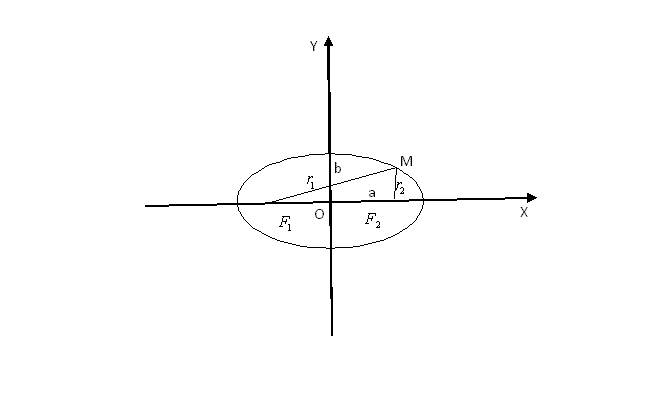

F1 , F2 – фокусы . F1 = ( c ; 0); F 2 (- c ; 0)

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

50. Гипербола и его параметры

Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния междуфокусами.

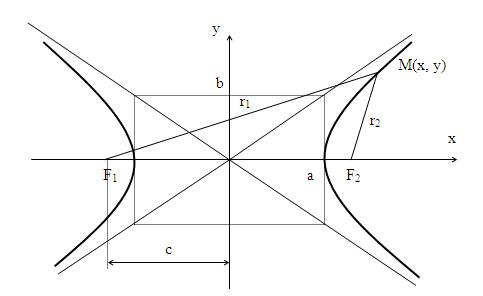
51. Парабола и его свойства

Пара́бола — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).

Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом. (у в квадрате = 2*р*х)

52. Постоянная и переменная велечина

Переменные величины — это такие величины, которые в условиях данного вопроса могут принимать различные значения

Постоянные величины — это такие величины, которые в условиях данного вопроса сохраняют неизменные значения.

53. О множестве. Основные понятия

Под множеством понимают объединение в одно целое объектов, связанных между собой неким свойством. Термин "множество" в математике не всегда обозначает большое количество предметов, оно может состоять из одного элемента и вообще не содержать элементов, тогда его называют пустым и обозначают Æ. Конечное множество состоит из конечного числа элементов, например, множество страниц в книге, множество студентов в группе и т.д.

Бесконечное множество состоит из бесконечного числа элементов, т.е. это множество, которое не является ни конечным, ни пустым. Например: множество действительных чисел, множество точек плоскости, множество атомов во Вселенной и т.д.

Счётное множество – множество, элементы которого можно пронумеровать. Например, множества натуральных, чётных, нечётных чисел. Счётное множество может быть конечным (множество книг в библиотеке) или бесконечным (множество целых чисел).

Несчётное множество – множество, элементы которого невозможно пронумеровать. Например, множество действительных чисел. Несчётное множество может быть только бесконечным.

Множества обычно обозначаются большими буквами А, В, С,…, а их элементы - малыми: а, в, с…