Где a, b, c - величины отрезков, отсекаемых плоскостью на осях координат. Уравнение плоскости "в отрезках"
Пусть
на координатных осях заданы точки 
и 
,
причем 
(рис.4.18).
Требуется составить уравнение плоскости,
проходящей через эти три точки.
Подставляя
в уравнение (4.21) координаты заданных
точек 
,
получаем:
Разделив
уравнение на 
,
получаем уравнение
(4.22) |
которое
называется уравнением
плоскости "в отрезках".
Говорят, что плоскость, проходящая через
точки 
и
, отсекает
на координатных осях "отрезки": 
на
оси абсцисс, 
на
оси ординат и 
на
оси аппликат. Разумеется, длины
отрезков 
и 
равны 
и 
соответственно.
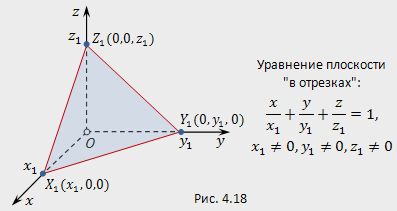
41. Нормальное уравнение плоскости
Уравнение Ax+By+Cz+D=0 плоскости, заданной относительно ПДСК, называется нормальным, если вектор n={A, B, C} перпендикулярен плоскости и |n|=1. Для того, чтобы общее уравнение плоскости привести к нормальному виду, достаточно обе части этого уравнения умножить на число M, чтобы (AM)2+(BM)2+(CM)2=1, то есть M=±1/√(A2+B2+C2), тогда нормальное уравнение плоскости имеет вид ±(Ax+By+Cz+D)/√(A2+B2+C2). В последнем уравнении знак перед дробью берется противоположно знаку коэффициента D.
Нормированное
уравнение, прямой на плоскости - уравнение
вида
где
- декартовы прямоугольные координаты
плоскости;
и
- координаты единичного вектора
перпендикулярного к прямой;
- расстояние от начала координат до
прямой. К Н. у. уравнение прямой вида
42. Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость. Если задано уравнение плоскости Ax + By + Cz + D = 0, то расстояние от точки M(Mx, My, Mz) до плоскости можно найти, используя следующую формулу
d = |A·Mx + B·My + C·Mz + D|
(A2 + B2 + C2)1/2
43. Угол между плоскостями.
Пусть плоскости α и β пересекаются по прямой с.
Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.
Другими словами, в плоскости α мы провели прямую а, перпендикулярную с. В плоскости β — прямую b, также перпендикулярную с. Угол между плоскостями α и β равен углу между прямыми а и b.
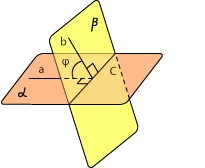
Условия перпендикулярности 2х плоскостей. Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, ВЕКТОР n1 * ВЕКТОР n2=0 или А1А2+В1В2+С1С2=0.
44. Приведение общего уравнения прямой к нормальному виду.
Уравнение и плоскость в данном контексте не отличаются друг от друга чем-то, кроме количества слагаемых в уравнениях и размерностью пространства. Поэтому сначала скажу все про плоскость, а в конце сделаю оговорку по поводу прямой.
Пусть дано общее уравнение плоскости: Ax + By + Cz + D = 0. Приведем его к нормальному виду. Для этого умножим обе части уравнения на нормирующий множитель М. Получаем: Мах+Мву+МСz+MD=0. При этом МА=cos, MB=cos;Mc=cos;. получаем систему:
М2 А2=cos2,
M2 B2=cos2;
M2 C2=cos2.
Сложив все уравнения системы, получаем М*(А2 +В2+С2)=1 Теперь остается только выразить отсюда М, чтобы знать, на какой именно нормирующий множитель надо умножить исходное общее уравнение для приведения его к нормальному виду:
M=-+1/КОРЕНЬ КВ А2 +B2 +C2
MD должен быть всегда меньше нуля, следовательно знак числа М берется противоположный знаку числа D.
С уравнением прямой все то же самое, только из формулы для М следует просто убрать слагаемое С2.