33. Общее уравнение прямой на плоскости.

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

•  C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

•  А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох

•  В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу

•  В = С = 0, А ≠0 – прямая совпадает с осью Оу

•  А = С = 0, В ≠0 – прямая совпадает с осью Ох

34. Уравнение прямой в отрезках

Если ни один из коэффициентов уравнения (1) не равен нулю, то его можно преобразовать к виду

, (2) где  ,   суть величины отрезков, которые отсекает прямая на координатных осях. Уравнение (2) называется уравнением прямой «в отрезках». Если две прямые даны уравнениями  и  , то могут представиться три случая:

а).   - прямые имеют одну общую точку;

б).   - прямые параллельны;

в).   - прямые сливаются, то есть оба уравнения определяют одну и ту же прямую.

35.Нормальное уравнение прямой

1. Нормальное уравнение прямой где p - длина перпендикуляра (нормали), опущенного из начала координат на прямую, а   - угол наклона этого перпендикуляра к оси Ox. Чтобы привести общее уравнение прямой Ax + By + C = 0 к нормальному виду, нужно все члены его умножить на нормирующий множитель  , взятый со знаком, противоположным знаку свободного члена C.

36 Расстояние между точкой и прямой.

вычисляется по следующей формуле: где x₀ и y₀ координаты точки, а A, B и С коэффициенты из общего уравнения прямой:

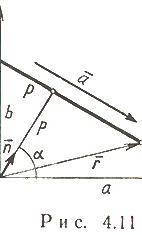
37.приведение общего уравнения прямой к нормальному вуиду.  Нормальное уравнение прямой (рис. 4.11) 

где   - угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.     Приведение общего уравнения прямой к нормальному виду:

Здесь   - нормируемый множитель прямой; знак выбирается противоположным знаку C, если   и произвольно, если C = 0.

38.Общее уравнение плоскости в пространстве.

Общим уравнением плоскости в пространстве называется уравнение вида

Ax + By + Cz + D = 0,

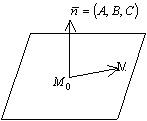
где A² + B² + C² ≠ 0 .  Определение. Вектор   перпендикулярен плоскости и называется ее нормальным вектором.

Если в прямоугольной системе координат    известны координаты трех точек  , не лежащих на одной прямой, то уравнение плоскости записывается в виде: 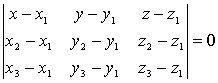 .Вычислив данный определитель, получим общее уравнение плоскости.

39.Уравнение плоскости проходящее через данную точку, и три данных точки.

Назовем нормалью к плоскости вектор, перпендикулярный к этой плоскости. Обозначают нормаль   (рис. 11).

 

Рис. 11

Определение. Уравнением поверхности в пространстве   называется такое уравнение между переменными   которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности.

Пусть точки   и   лежат на плоскости (рис. 11). Тогда   и, значит, их скалярное произведение равно нулю:   – это уравнение плоскости, проходящей через точку   перпендикулярно вектору  .

Укажем теперь основные уравнения плоскостей:

1)  – уравнение плоскости, проходящей через точку   перпендикулярно вектору  ;

2)   – общее уравнение плоскости (  – координаты нормали плоскости);

3) 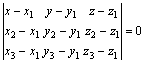  – уравнение плоскости, проходящей через три заданные точки  ,   и  ;

4)   – уравнение плоскости в отрезках, где   -величины направленных отрезков, отсекаемых плоскостью на координатных осях   и   соответственно.

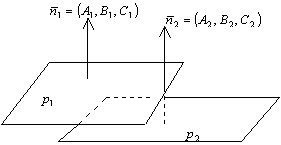
Если плоскости   и   параллельны или перпендикулярны друг к другу, то соответственно параллельны или перпендикулярны их нормальные векторы (рис. 12 и 13).

 

 

 

 

 

 Рис. 12

 

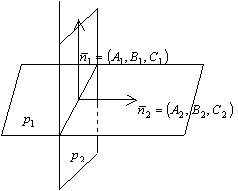
40.  Уравнение плоскости в отрезках