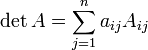РК 1

1. Определители 2го и 3го порядков.

Вычисление определителей второго порядка. Определитель второго порядка (матрицы размера 2 на 2) вычисляется по правилу: 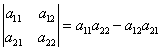Запомнить просто: произведение элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной.

Вычисление определителей третьего порядка. Определитель третьего порядка вычисляется по правилу: 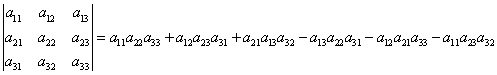Запомнить порядок сомножителей, конечно же, очень трудно, если не знать визуального представления этого правила, которое называется правило треугольников.

Правило Саррюса

2. Определитель н-го порядка

|a₁,₁ а₁,₂ … а₁,н |

| а₂,₁ а₂,₂ …..а₂,н|=|Aij| i,j=‾i,n‾

| ………………….. |

| а н,₁ а н,₂..а н,н|

Главная диагональ - с левого верхнего угла к правом нижнему, а побочная - с правого верхнего к левому нижнему.

Данное понятие определено только для двумерного массива, где число строк и столбцов совпадает (полjжим его n). Главная - диагональ в массиве от элемента [1,1] до элемента [n,n], т.е. [1,1], [2,2], [3,3] .. [n,n]  Побчная - диагональ в массиве от элемента [1,n] до элемента [n,1], т.е. [1,n], [2, n-1], [3, n-2] .. [n,1]

3. Правило Саррюса.

а11*а22*а33+а13+а21*а32+а12*а23*а31-а11*а23*а32-а13*а22*а31-а12*а21*а33

Закон составления выражения для определителя 3-го порядка весьма прост. Из членов, входящих со знаком +, один будет произведением элементов главной диагонали, каждый из двух других — произведением элементов, лежащих на параллели к этой диагонали, с добавлением третьего множителя из противоположного угла матрицы (рис. 252, а). Члены, входящие со знаком —, строятся таким же,образом относительно другой диагонали .Саррюса правило называют также правилом Саррюса или правилом диагоналей и треугольников.

Пример.

Задание. Вычислить определитель 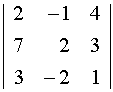  двумя способами:  а) разложением по элементам первой строки, б) по правилу Саррюса.

Решение. а) 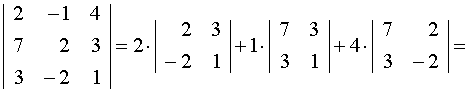   =2·(2·1-3·(-2)) + 1·(7·1-3·3) + 4(7·(-2)-3·2) = -66  б) 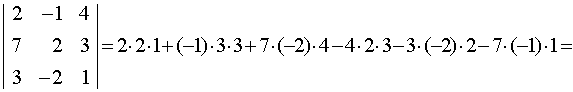 <  = 4 – 9 – 56 – 24 + 12 + 7 = -66

4. Когда определитель равен нулю:

1. Элементы какой либо строки или столбца-нули

2. Элементы двух параллельных строк или столбцов равны нулю

3. Элементы двух параллельных строк или столбцов пропорциональны

5. Основные свойства определителей.

1.1. Значение определителя не изменится, если:

- строки заменить на столбцы, такое действие называется транспонирование, т.е. действия, выполняемые со строками, справедливы и для столбцов;

- все элементы одной строки умножить на какое-либо число и прибавить к соответствующим элементам другой строки.

Такие действия с элементами определителя называются элементарными преобразованиями.

1.2. Определитель меняет знак на противоположный, если две каких-либо строки поменять местами.

6. Минор. Возьмём какой нибудь элемент Aij если вычеркнем i-тую строчку и j-тый столбец, то получим определитель н-1го порядка, полученный элемент называется минором элемента Aij и обозначается Mij.

Алгебраическое дополнение. Алгебраическим дополнением элемента Aij называется минор этого элемента, взятый со знаком (-1)^i+j и обозначается Aij=(-1)^i+j Mij

7. Сложение определителей. Каждый элемент некоторой строки(столбца) представляет собой сумму двух слагаемых,то определитель может быть представлен в виде в виде суммы двух определителей, причём в одном из них соответствующая строка (столбец) состоит из первых слагаемых, а в другом - из вторых слагаемых остальные же строки (столбцы) те же что и в исходном определителе.

Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k. Например,

.

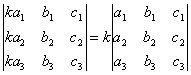8. Разложение определителя по элементам строки или столбца

Широко известен частный случай теоремы Лапласа — разложение определителя по строке или столбцу. Он позволяет представить определитель квадратной матрицы в виде суммы произведений элементов любой её строки или столбца на их алгебраические дополнения.

Пусть   — квадратная матрица размера  . Пусть также задан некоторый номер строки   либо номер столбца   матрицы  . Тогда определитель   может быть вычислен по следующим формулам:

Разложение по  -й строке: Разложение по  -му столбцу:

где   — алгебраическое дополнение к минору, расположенному в строке с номером   и столбце с номером  .   также называют алгебраическим дополнением к элементу  .

Утверждение является частным случаем теоремы Лапласа. Достаточно в ней положить   равным 1 и выбрать  -ую строку, тогда минорами, расположенными в этой строке будут сами элементы.

9. Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или у столбцов одинаковой длины). Матрица записывается в виде

или, сокращенно,A=(a_ij) (i=1,m, j=1,n) i-номер строки,(т.е.i=1,2,3..m),j-номер столбца.

Матрицу А называют матрицей размера  m x n  и пишут Аmxn.Числа a_ij составляющие матрицу, называются ее элементами. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ.

Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т. е.

А=В,если a_ij=b_ij  (i=1,m, j=1,n)

Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицуразмера n x n  называют матрицей n-го порядка.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой E.

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.

Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой O.

В матричном исчислении матрицы O и E играют роль чисел 0 и 1 в арифметике.

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называетсяматрицей транспонированной к данной. Обозначается А^Т

 

 Транспонированная матрица обладает следующим свойством: (А^Т)^Т=А

10. Сложение и умножение матриц.

Определение операции сложения двух матриц.

Операция сложения определена ТОЛЬКО ДЛЯ МАТРИЦ ОДНОГО ПОРЯДКА. Другими словами, нельзя найти сумму матриц разной размерности и вообще нельзя говорить о сложении матриц разной размерности. Также нельзя говорить о сумме матрицы и числа или о сумме матрицы и какого-нибудь другого элемента.

Определение.

Сумма двух матриц   и   - это матрица, элементы которой равны сумме соответствующих элементов матриц А и В, то есть,  .

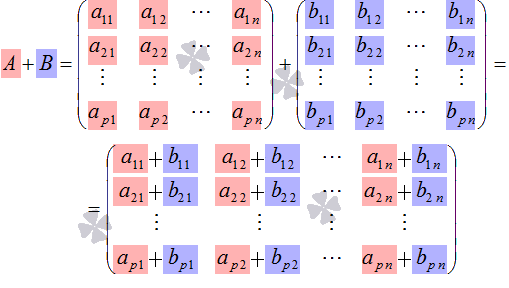
Таким образом, результатом операции сложения двух матриц является матрица того же порядка.

Определение операции умножения двух матриц.

Операция умножения двух матриц А и В определяется только для случая, когда ЧИСЛО СТОЛБЦОВ МАТРИЦЫ А РАВНО ЧИСЛУ СТРОК МАТРИЦЫ В.

Определение.

Произведение матрицы А порядка   и матрицы В порядка   - это такая матрица С порядка  , каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицыВ, то есть,

Таким образом, результатом операции умножения матрицы порядка   на матрицу порядка  является матрица порядка  .

11. Единичная и транспонированная матрицы.

Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно). Их вид:

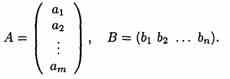
Матрица размера 1х1, состоящая из одного числа, отождествляется с этим числом,

т.е. (5)_1х1 есть 5.

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называетсяматрицей транспонированной к данной. Обозначается А^Т

 

12.Обратная матрица. Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

13. Системой   линейных алгебраических уравнений с   неизвестными называется система уравнений вида

A₁₁X₁+A₁₂X₂+….+A₁nXn=b₁

A₂₁X₁+A₂₂X₂+….+A₂nXn=b₂

Am₁X₁+Am₂X₂+….+AmnXn=bm

Числа   называются коэффициентами системы;   — свободными членами,   —неизвестными. Количество   уравнений в системе может быть меньше, больше или равно числу   неизвестных.

Решением системы называется упорядоченная совокупность   чисел   такая, что после замены неизвестных  соответственно числами   каждое уравнение системы превращается в верное числовое равенство. Система называется совместной, если она имеет хотя бы одно решение. Если система не имеет ни одного решения, то она называется несовместной.

Система (5.1) называется однородной, если все свободные члены равны нулю:

В отличие от однородной, систему общего вида (5.1) называют неоднородной.

14. Метод Крамера. Для системы   линейных уравнений с   неизвестными (над произвольным полем)

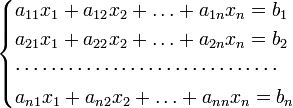
с определителем матрицы системы  , отличным от нуля, решение записывается в виде

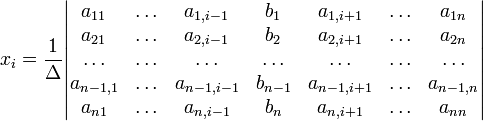
(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

В этой форме формула Крамера справедлива без предположения, что   отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца(определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы   и  , либо набор   состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом.

Пример:

Система линейных уравнений:

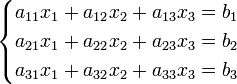
Определители:

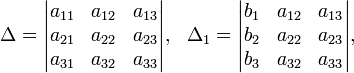
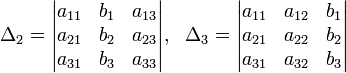
Решение:

Пример:

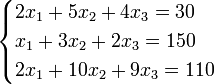
Определители:

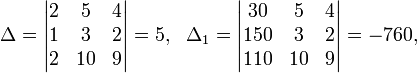
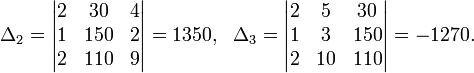
15. Матричный метод решения СЛАУ.

Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с   неизвестными (над произвольным полем):

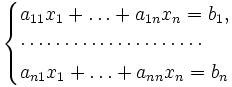
Тогда её можно переписать в матричной форме:

, где   — основная матрица системы,   и   — столбцы свободных членов и решений системы соответственно:

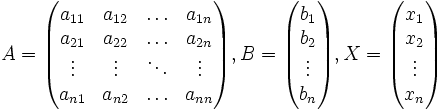
Умножим это матричное уравнение слева на   — матрицу, обратную к матрице  : 

Пример:

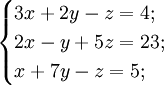
Сначала убедимся в том, что определитель матрицы из коэффициентов при неизвестных СЛАУ не равен нулю.

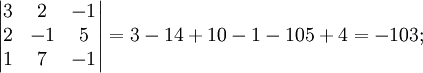
Теперь вычислим алгебраические дополнения для элементов матрицы, состоящей из коэффициентов при неизвестных. Они нам понадобятся для нахождения обратной матрицы.

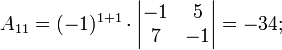
Далее найдём союзную матрицу, транспонируем её и подставим в формулу для нахождения обратной матрицы.

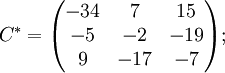
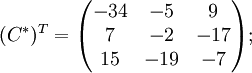
Подставляя переменные в формулу, получаем:

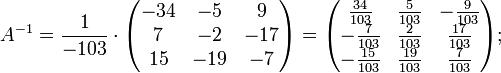
Осталось найти неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов.

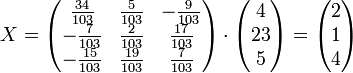
Итак, x=2; y=1; z=4.

16. Декартова система координат.

Системой координат называется совокупность одной, двух, трех или более пересекающихся координатных осей, точки, в которой эти оси пересекаются, – начала координат– и единичных отрезков на каждой из осей. Каждая точка в системе координат определяется упорядоченным набором нескольких чисел – координат. В конкретной невырожденной координатной системе каждой точке соответствует один и только один набор координат.

Если в качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной (или ортогональной). 

Полярная система координат на плоскости.

Возьмем на данной плоскости произвольную точку О и назовем её полюсом. Проведем на данной плоскости из точки О направленный луч, который назовем полярным лучом. Пусть М – произвольная точка данной плоскости. Соединим точку М с полюсом отрезком прямой и назовем этот отрезок ОМ и его длину   полярным радиусом точки М. Уголповорота   полярного луча вокруг полюса против часовой стрелки до совпадения с полярным радиусом точки М назовем полярным углом точки М.

                     

                                        рис.1.

Определение. Упорядоченная пара действительных чисел   называется полярными координатами точки М.

Определение. Полярной системой координат на плоскости называется полюс и полярный луч вместе с понятием полярных координат любой точки плоскости.

Замечание. Полярные координаты однозначно определяют положение любой точки на плоскости, за единственным исключением – самого полюса. Чтобы восстановить однозначность для любой точки плоскости полагают полярные координаты полюса равными нулю:

О(0; 0). Полярный угол рассматривают в пределах одного оборота и, как в тригонометрии, поворот против часовой стрелки считают положительным, а по часовой стрелке – отрицательным. Чаще всего полагают, что полярный угол  .

17. Связь полярной системы координат с ПДСК.

Пару полярных координат   и   можно перевести в Декартовы координаты   и   путём применения тригонометрических функций синуса и косинуса:

в то время как две декартовы координаты   и   могут быть переведены в полярную координату  :

 (по теореме Пифагора).

Для определения угловой координаты   следует принять во внимание два следующие соображения:

Для  ,   может быть произвольным действительным числом.

Для  , чтобы получить уникальное значение  , следует ограничиться интервалом в  . Обычно выбирают интервал   или  .

Для вычисления   в интервале  , можно воспользоваться такими уравнениями (  обозначает обратную функцию к тангенсу):

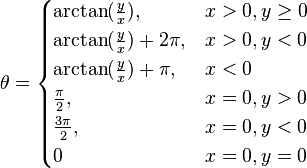
Для вычисления   в интервале  , можно воспользоваться такими уравнениями:^[14]

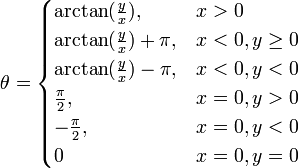
18. Вектор-направленный отрезок

=|‾a|

Модуль вектора

x=|‾a|cosA cosA=x/V‾x²+y²+z² |‾a|= V‾x²+y²+z²

вводим 3 взаимно перпендикулярных единичных вектора, приложенных к началу координат и направленных по осям тогда

i,j,k-орты ‾а=х*‾ i+y*‾j+z*‾k

19. Сложение, вычитание и умножение векторов

Суммой двух векторов   и   называется вектор  , направленный из начала вектора  в конец вектора   при условии, что начало  совпадет с концом вектора  . Если векторы заданы их разложениями по базисным ортам, то при сложении векторов складываются их соответствующие координаты.

Разностью векторов   и   называют вектор  Второе слагаемое является вектором, противоположным вектору   по направлению, но равным ему по длине.

Таким образом, операция вычитания векторов заменяется на операцию сложения.

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними, т.е.

Из определения следует

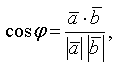
где φ - угол между векторами.

20. Направляющие косинусы векторов.

Направляющие косинусы вектора ‾a – это косинусы углов, которые вектор образует с положительными полуосями координат.

Чтобы найти направляющие косинусы вектора ‾a

 необходимо соответствующие координаты вектора поделить на модуль вектора.

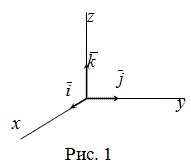
21. Разложение вектора по ортам.

Система ортов (или базисная система векторов) - это система единичных векторов осей координатОрт координатной оси   обозначается через  , оси   - через  , оси   - через  (рис. 1).

.

Для любого вектора   , который лежит в плоскости   , имеет место следующее разложение: 

Если вектор   расположен в пространстве, то разложение по ортам координатных осей имеет вид: 

Вектор - это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Если А — начало вектора, а В - его конец, то вектор обозначается символом АВ или а. Вектор ВА (у него начало в точке В, а конец в точке A ) называется противоположным векторуАВ . Вектор, противоположный вектору а , обозначается -а .

22.Скалярное произведение векторов

Скалярное произведение векторов — это число, равное произведению длин этих векторов на косинус угла между ними.

.

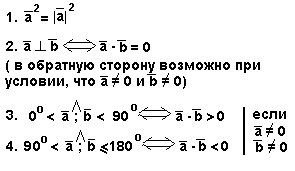Скалярное произведение векторов через их координаты

23.Угол между двумя векторами

Угол между векторами — угол между направлениями этих векторов (наименьший угол).

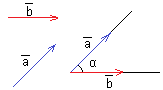
По определению, угол между двумя векторами находится в промежутке [0°; 180°]. Угол между векторами   обозначается так:  . Если векторы перпендикулярны, то угол между ними равен 90º. Если векторы сонаправлены, в частности один из них или оба нулевые, то угол между ними равен 0^о. Если противоположно направленные векторы, то угол между ними равен 180º. Угол между двумя ненулевыми векторами находится с помощью вычисления скалярного произведения. По определению скалярное произведение равно произведению длин векторов на косинус угла между ними (скалярное произведение для двух векторов с координатами (x₁; y₁) и (x₂; y₂) вычисляется по формуле: x₁x₂ + y₁y₂).

24.Условие парелельности и перпендикулярности двух векторов

Условие перпендикулярности векторов

• Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.

• Даны два вектора a (xa;ya) и b (xb;yb). Эти векторы будут перпендикулярны, если выражение x_ax_b + y_ay_b = 0.

Два ненулевых вектора называются перпендикулярными, если угол между ними равен девяноста градусам (  радиан).Если от некоторой точки плоскости отложить векторы равные заданным векторам, то с помощью транспортира можно измерить угол между ними. Это позволит с некоторой степенью точности установить перпендикулярность векторов (если при измерении получили угол девяносто градусов). При этом конечно же следует учитывать точность построения и точность измерения. Такой метод для определения перпендикулярности двух векторов следует использовать только тогда, когда мы ничего не знаем об этих векторах, а имеем только их изображение на плоскости.

Теорема.Для перпендикулярности двух ненулевых векторов   и   необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство  .

Доказательство.

Пусть векторы   и   перпендикулярны. Докажем выполнение равенства  .

По определению скалярное произведение векторов равно произведению их длин на косинус угла между ними. Так как векторы   и   перпендикулярны, то угол между ними равен девяноста градусам, следовательно, 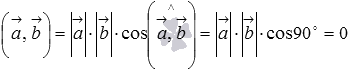 , что и требовалось доказать.

Переходим ко второй части доказательства.

Теперь считаем, что  . Докажем, что векторы   и   перпендикулярны.

Так как векторы   и   ненулевые, то из равенства 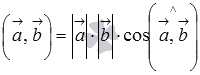  следует, что 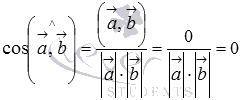 . Таким образом, косинус угла между векторами  и   равен нулю, следовательно, угол 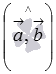  равен  , что указывает на перпендикулярность векторов   и  .

Итак, необходимое и достаточное условие перпендикулярности двух векторов полностью доказано.

Условие паралельности:

25.Векторные проихведения двух векторов

26.Коллинеарные и компланарные векторы.Два вектора, параллельные одной прямой, называются коллинеарными. Два ненулевыхколлинеарных вектора либо одинаково, либо противоположно направлены. Нулевой вектор считаетсяколлинеарным любому вектору. Теорема 1. Если векторы −→a и −→b коллинеарны и −→a/=−→0 , то существует  единственное число α такое, что −→b=α−→a. Векторы −→a,−→b и −→c называются компланарными, если существует плоскость, которой они  параллельны. Теорема 2. Если векторы −→a,−→b и −→c компланарны, а векторы −→a,−→b не коллинеарны, то существуют единственные числа α и β такие, что −→c=α−→a+β−→b.

Рассмотрим систему векторов −−→a1,−−→a2,...,−−→an и зададим n действительных чисел α1,α2,...,αn. Вектор −→b=α1−−→a1+α2−−→a2+...+αn−−→an называется линейной комбинацией данных векторов −−→a1,−−→a2,...,−−→an. Система векторов −−→a1,−−→a2,...,−−→an называется линейно зависимой, если существуют числа α1,α2,...,αn, среди которых хотя бы одно отлично от нуля, и такие что α1−−→a1+α2−−→a2+...+αn−−→an=−→0.  Если же равенство α1−−→a1+α2−−→a2+...+αn−−→an=−→0 справедливо только при α1=α2=...=αn=0, то система векторов −−→a1,−−→a2,...,−−→an называется линейно независимой.