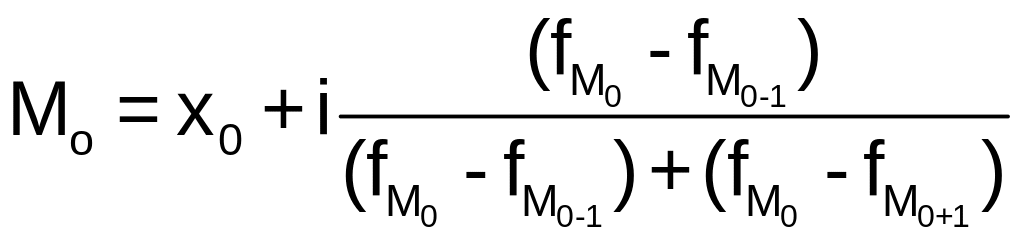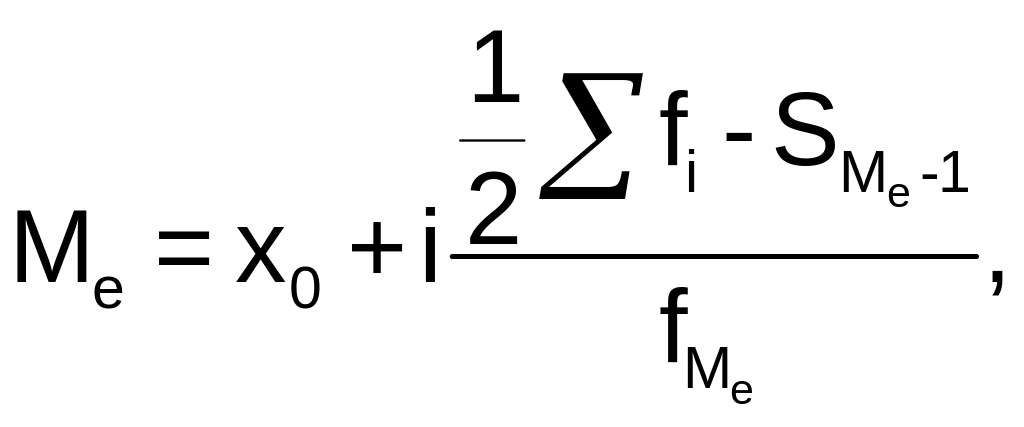Тема 5. Анализ рядов распределения
Цель – закрепление теоретического и практического материала по теме «Анализ рядов распределения».
Задача – провести анализ статистических рядов распределения, предоставить экономическую интерпретацию рассчитанным показателям
Методические рекомендации
Основные формулы для расчета характеристик рядов распреде-ления представлены в табл. 33.
Таблица 33
Формулы для расчета характеристик рядов распределения
Мода |
|
Медиана |
|
Дисперсия |
|
Среднее квадратическое отклонение |
|
Коэффициент вариации |
|
Средняя из внутрегрупповых дисперсий |
|
Межгрупповая дисперсия |
|
Общая дисперсия |
|
Коэффициент детерминации |
|
Дисперсия альтернативного признака |
|
Типовая задача
Задача 1
Имеем данные о распределении частных автомобилей п. Кома-ровка за сроком работы до капитального ремонта (табл. 34). Определите:
1. Показатели центральной тенденции.
2. Показатели вариации.
3. Показатели асимметрии и эксцесса.
Таблица 34
Распределение автомобилей за сроком службы
Группы по срокам работы к капитальному ремонту |
Количество автомобилей, ед. |
Накопленные частоты |
0 3 |
43 |
43 |
3 6 |
56 |
99 |
6 9 |
48 |
147 |
9 12 |
32 |
179 |
12 15 |
18 |
197 |
Всего |
197 |
|
Решение
Для расчета показателей целесообразно составить вспомогате-льную таблицу (табл. 35).
Таблица 35
Таблица расчетов
Группы по срокам работы к капитальному ремонту |
Середи-на интерва-ла, xi |
Количе-ство автомоби-лей, fi |
Накоплен-ные частоты, S |
xifs |
|
|
|
||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
||||
0 3 |
1,5 |
43 |
43 |
64,5 |
4,87 |
23,72 |
1019,96 |
||||
3 6 |
4,5 |
56 |
99 |
252 |
-1,87 |
3,50 |
196 |
||||
Окончание табл. 35
|
|
|
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
||||
6 9 |
7,5 |
48 |
147 |
360 |
1,13 |
1,28 |
61,44 |
||||
9 12 |
10,5 |
32 |
179 |
336 |
4,13 |
17,06 |
545,92 |
||||
12 15 |
13,5 |
18 |
197 |
243 |
7,13 |
50,83 |
914,94 |
||||
Всего |
|
197 |
|
1255,5 |
|
|
2738,26 |
||||
лет
– средний срок работы.
Для определения моды и медианы в интервальном ряде сначала находят интервал, который содержит эти показатели, а потом рассчитывают конкретные значения этих показателей.
Модальным интервалом в данном случае будет интервал 3 6 лет, поскольку наибольшее количество автомобилей находится в этом интервале. Мода будет равна:
Итак в исследуемой совокупности наибольшее количество автомобилей имеет срок работы к капитальному ремонту 4,86 лет.
Медианным интервалом также будет интервал 3 6, так как середина вариационного ранжированного ряда (98,5) находится по накопленным частотам там, где их сумма равна 99. Медиана будет составлять:
лет.
Итак, срок работы автомобилей равен 5,97 лет и является той вариантой которая делит вариационный ряд распределения на две равные части (98 автомобилей имеют срок работы ниже 5,97 лет и 99 автомобилей свыше 5,97 лет).
Среднее квадратичное отклонение будет составлять:
года.
Средний срок работы составляет 6,37 года, а среднее отклонение, которое показывает, как в среднем отклоняются индивидуальные значения признака от средней арифметической, равно 3,73 года.
Коэффициент вариации:
или
58,5 %.
Соответственно полученным результатам, совокупность не является однородной, так как полученное значение коэффициента вариации больше порогового значение 33 %.
Для определения формы распределения необходимо определить показатель асимметрии:
.
Асимметрия правосторонняя, так как показатель имеет положительный знак.
Рассчитаем коэффициент эксцесса:
,
где М4 – центральный момент четвертого порядка;
;
;
.
Отрицательное значение показателя эксцесса свидетельствует о плосковершинности распределения.
Проведенные расчеты подтверждаются общим видом распределения (рис. 1.1).
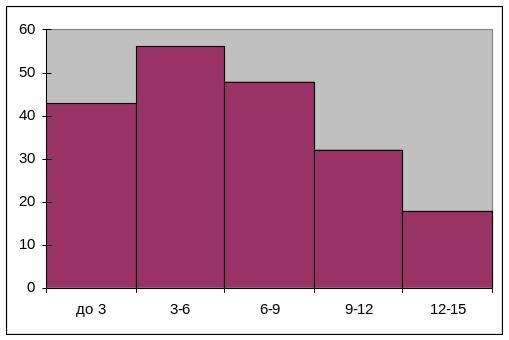
Рис. 1.1. Общий вид распределения