12. Связь разностного уравнения и z-преобразования.

Разностное уравнение описывает реальные действия, которые система дискретного времени должна над сходными данными во временной области, чтобы получить необходимый выход.

13. Цифровые фильтры. Виды цифровых фильтров.

Цифровые фильтры могут реализовывать возможности недоступные Аналоговым:

• Уровень затухания в аналоговых фильтрах ограничен

• Один фильтр может использовать несколько входных данных

• Используется для очень низких частот

• Уровень затухания определяется разрядностью

Недостатки:

• Ограниченная скорость

• Влияние конечной разрядности

  • Квантование коэффициентов

  • Потеря устойчивости (БИХ)

  • Ошибки округления

  • Шум округления

  • Переполнение

Фильтр с конечной импульсной характеристикой:

Фильтр с бесконечной импульсной характеристикой:

14. Сравнение ких и бих фильтров.

• БИХ – близки к Аналоговым фильтрам и используются для АЦП

• КИХ фильтр имеет большее количество коэффициентов нежели БИХ (следовательно БИХ быстрее)

• КИХ обеспечивают линейность ФЧХ

• БИХ обеспечивают нелинейность ФЧХ

• КИХ не рекуррентен (если пропустить сигнал через фильтр в обратном направлении то он не изменится)

• БИХ рекуррентен

15. Спецификация требований к фильтрам.

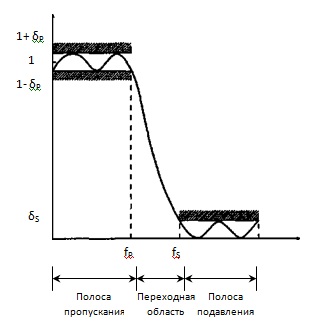
Спецификация требований включает спецификации 1)      Характеристик сигналов 2)      Характеристик фильтра (АЧХ, ФЧХ, скорость работы и режимы фильтрации); 3)      Принципа реализации (на базе ПК или в МК) 4)      Других требований к структуре (например, стоимость фильтра).

Ширина полосы перехода определяет, насколько резким является характеристика фильтра. В этой области амплитудная характеристика монотонно уменьшается от полосы пропускания до полосы подавления.  

 

16. Линейная фазовая характеристика и ее следствия.

Линейный ФЧХ обеспечивает постоянную групповую задержку (не меняется при изменении частоты).

Задержки сигнала:

• Фазовая – задержка по времени которую испытывает каждый частотный компонент сигнала проходя через фильтр

• Групповая – средняя задержка составного сигнала.

Если БИХ фильтр обладает положительной симметрией (h – четная), то

,

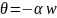Если БИХ фильтр обладает отрицательной симметрией (h – нечетная), то

,

17. Принципы расчета характеристик ких фильтра методом взвешивания.

Поскольку частотная характеристика любого цифрового фильтра  является периодической функцией частоты, ее можно представить рядом Фурье.

Лучшие результаты, дает метод проектирования КИХ-фильтров, основанный на использовании весовой последовательности конечной длины , называемой окном, для модификации коэффициентов Фурье h(n) в формуле с тем, чтобы управлять сходимостью ряда Фурье. Для большинства приемлемых окон функция  имеет главный лепесток, содержащий почти всю энергию окна, и боковые лепестки, которые обычно быстро затухают. 

18. Принципы расчета характеристик КИХ фильтра оптимизационными методами.

Задача оптимизации состоит в том, чтобы МИНимизировать МАКСимальную ошибку (отклонение)

- функция ошибки

W(w) – весовая функция

H_D – идеальная импульсная характеристика

H – реальная импульсная характеристика

19. Принципы расчета характеристик КИХ фильтра методам частотной выборки.

C помощью обратного преобразования Фурье находим импульсную хар-ку:

Н(к) – выборка из идеальной частотной характеристики

Чтобы избежать неравномерностей в импульсную хар-ку добавляют точки (чем больше точек, тем меньше неравномерностей).

20. Эффекты конечной разрядности в цифровых фильтрах.

1. Шум квантования (шум АЦП):

– мощность квантования

шаг квантования

разрядность

импульсная хар-ка

2. Влияние структуры фильтра:

   1. Прямая форма:

(+) малая вероятность переполнения т.к. один сумматор

(+) округлять проще т.к. один сумматор

2. Обратная форма (наверное)

3. Переполнение:

Для решения проблемы переполнения применяют масштабирование, но при этом уменьшается отношение (сигнал / шум).

Масштабирование: входной сигнал делять на коэффициент S_1, а выходной умножают на данный коэффициент.

Норма l₁ : - гарантирует отсутствие переполнения

Норма l₂ :

Норма : - максимум от спектра амплитудной хар-ки.

21. Подавления эхосигналов в линии передачи.

Задача минимизировать ошибку Е:

N – количество коэффициентов фильтра

22. В чем заключается обобщенная линейная или гомоморфная обработка

Гомоморфная фильтрация - это обобщенная техника для цифровой обработки сигналов

23. Модель речевых сигналов

24. В чем сущность метода линейного предсказания при сжатии речевых сигналов

25. Сокращение избыточности изображений методом линейного предсказания