1. Ортогональные и ортонормированные системы функций. Ортонормированный базис.

Функции ортогональны – если их скалярное произведение равно 0.

Функции нормированы – если их скалярное произведение равно 1.

Система функций ортогональная – если все ее функции не исчезают тождественно и попарно ортогональны

Система функций ортонормированная – если она ортогональная и произведение функции самой на себя равно 1.

Ортонормированная система является ортонормированный базисом на рассматриваемом интервале, если ряд Фурье любой квадратично-интегральной функции сходится в среднем к этой функции на рассматриваемом интервале.

2. Периодическая функция – это функция повторяющаяся через какой-то интервал времени: F(x) = F(x + n T)

3. Что такое ряд Фурье. Гармоника.

Ряд Фурье функции – это разложение данной функции ортогональным базисом.

Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -Pi ≤ X ≤ Pi можно выразить в виде сходящихся тригонометрических рядов.

Разложение в ряд Фурье – это функциональный ряд вида:

(1)

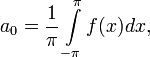
** ТЕОРЕМА О СХОДИМОСТИ **

Если функция непрерывна на интервале (-PI, PI), то ряд Фурье в этом интервале сходится!

Гармоника – это элементарная составляющая гармонического колебания.

Гармонические колебания имеют вид:

А – амплитуда

W – угловая частота

- начальная фаза

Ряд Фурье можно представить в виде суммы бесконечного числа гармоник:

U_{0 ­}– нулевая гармоника

К – номер гармоники

K*W – угловая частота К-ой гармоники = k * 2 * PI / T

4. Что такое частотные спектры. Какие они бывают.

Спектр – это совокупность гармоник, образующих исходный сигнал.

Частотный спектр – это совокупность коэффициентов a, b комплексного числа ряда Фурье

Типы спектров: дискретный, непрерывный, и наложение дискретных и непрерывных.

5. Что такое интеграл Фурье. Как связан интеграл Фурье с рядом Фурье.

Интеграл Фурье, который можно считать обобщением ряда Фурье на случай непериодической действительной функции, определённой на вей числовой прямой.

6. В чем заключается дискретизация и квантование непрерывных процессов.

Дискретизация – это определение значений непрерывного сигнала в дискретный момент времени.

Процесс дискретизации можно рассматривать как аналогового сигнала на выборочную функцию, которая состоит из импульсов единичной Амплитуды, с бесконечно малой шириной и периодом Т (равному частоте дискретизации)

Чтобы элементы выборки полностью описывали сигнал, частота дискретизации должна быть больше 2 * F_MAX.

Квантование – разбиение диапазона значений на конечное число интервалов, округление величины отсчета.

Шаг квантования равен: n – разрядность квантования

Каждый отсчету сигнала присваивается значений интервала в который попадает значение сигнала. Номер интервала – это двоичное число с разрядностью n. Таким образом входной (аналоговый) сигнал представляется последовательностью двоичных чисел. При этом каждое двоичное число представляется последовательностью импульсов высокого (1) и низкого (0) уровня