4. Системы эконометрических уравнений: виды, оценка параметров, области применения на практике.

Для описания реальных экономических систем, где статистические показатели находятся во взаимодействии и взаимосвязи, возникают сложности со спецификацией модели, поскольку многие факторные и результативные признаки взаимодействуют друг с другом. Из-за этого возникает проблема мультиколлинеарности факторов в уравнениях множественной регрессии. Одна и та же переменная может рассматриваться как факторная, независимая, а с другой – как результативная, случайная величина. Случайные переменные называют эндогенными, т.е. внутренними, так как они формируют свои значения внутри модели. Признаки, считающиеся заданными, известными, неслучайными получили название экзогенных, или внешних для данной системы. Один и тот же признак может быть эндогенным в одной задаче и экзогенным – в другой.Далее будем обозначать экзогенные переменные х, а эндогенные – у.

В зависимости от характера взаимосвязей между эндогенными и экзогенными переменными выделяют: системы рекурсивных (рекуррентных) и совместных, одновременных, взаимосвязанных уравнений.

Отличие между ними заключается в том, что в системе совместных уравнений одни и те же признаки одновременно могут выступать и в роли зависимых и в роли независимых переменных. Т.е. зависимые переменные входят в одних уравнениях в левую часть, в других – в правую часть системы:

В эконометрике такая система уравнений называется также структурной формой модели.

Структурная форма модели содержит при эндогенных переменных коэффициенты , экзогенных переменных – 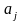, которые называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях от среднего уровня:В общем виде модель системы рекурсивных уравнений будет иметь вид:

В системе рекурсивных уравнений хоты бы одна эндогенная переменная должна определятся только лишь набором независимых переменных. Если все эндогенные переменные расположены в левой части, а экзогенные – в левой, то такая система называется системой независимых уравнений. Для решения систем независимых и рекурсивных переменных используется метод наименьших квадратов.Методы оценивания параметров систем одновременных уравнений рассмотрим далее.

Косвенный МНК

Препятствие к применению метода наименьших квадратов, которое заключается в коррелированности эндогенных переменных со случайными членами легко преодолеть, если:

1. привести систему к виду, чтобы в правой части оставались только экзогенные переменные. Такая форма называется приведенной;

2. затем применить метод наименьших квадратов к каждому уравнению в приведенной форме и получить оценки ее параметров;

3. перейти от приведенной формы к структурной, проведя процедуру обратного преобразования параметров.

Эта методика получила название косвенного метода наименьших квадратов и позволяет получать состоятельные и несмещенные оценки параметров структурной форму системы одновременных уравнений.

5. Экономическое моделирование основной тенденции развития временного ряда, взаимосвязей на основе данных временных рядов.

Метод аналитического сглаживания для выявления тенденции в рядах динамики применим только для качественно однородных периодов. Если ряд содержит структурные изменения, то выявлять тенденцию следует по подпериодам: до t* и после t*.

Для оценки возможности построения тренда по данным всего ряда без разбиения на подпериоды используется тест Чоу. Выдвигается гипотеза о том, что вектор оценок параметров (т.е. оценки всех параметров) тренда по первому подвериоду равен вектору по второму подпериоду, также о равенстве остаточных дисперсий отклонений от линий трендов по этим подпериодам: Н₀: .

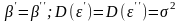Тест Чоу:

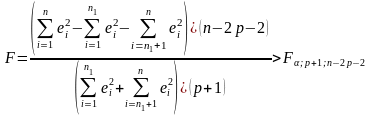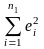, где р – число параметров без свободного члена, - остаточная сумма квадратов при построении тренда по всей совокупности. , - остаточные суммы квадратов для первого и второго подпериодов.

Выбор формы тренда можно осуществить с помощью теста на различие в остаточных дисперсиях:

.

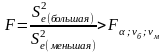Критическое значение находят при выбранном уровне значимости ( ) и числе степеней свободы для большей (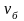 ) и меньшей ( ) из двух дисперсий.

В случае выполнения неравенства делается заключение о том, что различия в дисперсиях существенны и функция, которой соответствует меньшая дисперсия, действительно лучше аппроксимирует исходные значения, и именно она выбирается для описания тенденции. Иначе, предпочтение отдается более простой функции.

Средняя ошибка прогноза линейного тренда рассчитывается по формуле: .

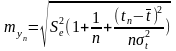Изучение взаимосвязи экономических переменных по данным временных рядов осложнено тем, что в этих рядах может быть тенденция. Чтобы выявить причинно-следственную зависимость между переменными, необходимо устранить ложную корреляцию между ними, вызванную наличием тенденции.

Существует несколько способов исключения тенденции в рядах динамики. Первый способ называется метод отклонений от тренда. Пусть имеется у_t= Т + е и х_t= Т + е. Проводится аналитическое выравнивание каждого ряда: 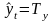и , где Т_у и Т_х – это оценки трендовых компонент. Затем определяется остаток в каждом наблюдени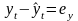и и

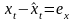, так как остаточная компонента не содержит тенденции. Далее изучается зависимость между самими остатками е_у=f(е_х). Если между переменными есть связь, то она проявится в согласованном изменении остатков. Недостатком данного способа является то, что содержательная интерпретация параметров такой модели затруднительна. Однако модель может быть использована для прогнозов и, кроме того, коэффициент парной корреляции между остатками отразит связь переменных.

Второй способ преодоления тенденции в рядах динамики – это метод последовательных разностей. Если временной ряд содержит ярко выраженную линейную тенденцию, то для ее устранения можно заменить исходные уровни разностями первого порядка, то есть цепными абсолютными приростами: и 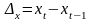. Далее прирост у рассматривается как функция прироста х: .

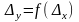Третьим способом является включение в модель регрессии фактора времени: y_t= a+b₁x₁+ b₂ t. Коэффициент b₁ покажет на сколько единиц изменится результат при единичном изменении фактора при условии существования неизменной тенденции; коэффициент b₂ отразит влияние всех прочих факторов, формирующих тенденцию, кроме x₁. Однако данный способ построения регрессионной модели требует большего объема наблюдений.

Однако при моделировании временных рядов встречаются ситуации, когда остатки содержат тенденцию или цикличность. В этом случае остатки не являются независимыми, каждое последующее значение остатка зависит от предыдущего. Это явление получило название автокорреляция остатков.

Существуют два способа определения автокорреляции в остатках. Первый заключается в визуальном анализе графика зависимостей остатков от времени. Второй способ предполагает использование критерия Дарбина-Уотсона. Величину критерия (d) можно определить по одной из формул

либо d 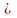2(1 – r_e¹)

где r_e¹ – коэффициент автокорреляции остатков первого порядка.

Если в остатках существует полная положительная автокорреляция, то r_e¹=1 и d = 0. Если в остатках полная отрицательная автокорреляция, то

r_e¹=-1 и d = 4. Если автокорреляция остатков отсутствует, то r_e¹=0 и d = 2.

На практике используется следующий алгоритм проверки гипотезы об автокорреляции остатков:

1. выдвигается нулевая гипотеза об отсутствии автокорреляции в остатках;

2. 2 определяется фактическое значение критерия Дарбина – Уотсона (d);

3. по специальным таблицам (приложение учебника по эконометрике) находят критические значения критерия d_L и d_u , где п –число наблюдений, k- независимых переменных в модели, 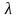- уровень значимости;

4. числовой промежуток всех возможных значений d разбивается на 5 отрезков

Есть положи-тельная автокорре-ляция остатков

Зона неопределенности

Автокорреля-ция остатков отсутствует

Зона неопределенности

Есть отрицательная автокорреляция остатков

0 d _L d _u 2 4- d _u 4 - d _L 4

5. если d - фактическое попадает в зону неопределенности, то предполагают существование автокорреляции в остатках.