2. Прогноз и оценка его точности на основе уравнений парной и множественной линейной регрессии.

При использовании уравнения множественной регрессии в целях прогнозирования, необходимо давать точечную и интервальную оценку полученных прогнозных значений зависимой переменной.

Средняя ошибка прогноза ( ) зависит от среднеквадратического отклонения индивидуальных значений от выравненных по уравнению регрессии S_e и ошибки положения гиперплоскости регрессии при экстраполяции факторных признаков.

Доверительный интервал прогноза имеет вид:

.

При оценке прогноза предпочтительнее проводить интервальное оценивание, поскольку вероятность осуществления точечного прогноза невелика.

Одним из показателей качества модели является средняя ошибка аппроксимации:

Средняя ошибка аппроксимации не превышает 10%, поэтому уравнение можно считать приемлемым для прогнозирования.

Средняя ошибка прогноза =Sсл

Предельная ошибка: ε= * t.

Интервальная оценка: с уровнем доверия 95% .

3. Нелинейные модели парной и множественной регрессии. Производственные функции.

Производственной функцией называется экономико-математическая модель, с помощью которой можно охарактеризовать зависимость результатов производственной деятельности предприятия, отрасли или национальной экономики в целом от повлиявших на эти результаты факторов.

Основными разновидностями однофакторных производственных функций являются:

1) линейная однофакторная производственная функция вида:

y=β0+β1x,

2) параболическая однофакторная производственная функция вида:

;при условиях β0›0, β1›0, β2›0.

Данная функция характеризуется тем, что при росте затрат ресурса х, объём произведённой продукции у вначале возрастает до некоторой максимальной величины, а затем снижается до нуля;

3) степенная однофакторная производственная функция вида:

; при условиях β0›0, β1›0.

Данная функция характеризуется тем, что с ростом затрат ресурса х, объём производства у возрастает без ограничений;

4) показательная однофакторная производственная функция вида:

; при условиях 0‹β1‹0.

Данная функция характеризуется тем, что с ростом затрат ресурса х объём произведённой продукции у также растёт, стремясь при этом к значению параметра β0.

5) гиперболическая однофакторная производственная функция вида: 

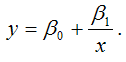
Данная функция практически не применяется при изучении зависимости объёма производства от затрат какого-либо ресурса, потому что нет необходимости в изучении ресурсов, увеличение которых приводит к уменьшению объёма производства.

Двухфакторные производственные функции (функции с двумя факторными переменными) характеризуют зависимость объёма производства от каких-либо двух факторов, чаще от факторов объёма основного капитала и трудовых ресурсов. Чаще всего используются такие двухфакторные производственные функции как функции Кобба-Дугласа и Солоу.

Для наглядного изображения двухфакторных производственных функций строят графики семейства кривых, основанных на различном сочетании двух факторов, но дающих в результате одно и то же значение объёма выпуска продукции. Кривые, построенные на основании равенства f(x1,x2)=const, называются изоквантами.

Два класса нелинейных регрессий:

1. регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам. Примером этого класса моделей могут служить полиномы разных степеней у = а + вх + сх²; у = а + вх + сх²+ dх³, а также равносторонняя гипербола

у = в + а/х.

2. нелинейные регрессии по оцениваемым параметрам:

• степенная у = а х^в

• показательная у = а в^х

• экспоненциальная у = е ^{а+ вх}.