Решение:

Вариант I решения: Рассматриваемый механизм находится под действием следующей системы уравновешивающихся сил: силы упругости , сил тяжести вала 1 с шестерней 2, шестерни 3, ползуна В, груза и реакций опор.

Составим уравнение работ, выражающее принцип возможных перемещений:

Связи наложенные на механизм, допускают следующие возможные перемещения его звеньев: поворот вала 1 с шестерней 2 на угол , поворот шестерни 3 на угол и поступательное перемещение груза по вертикали на . Ползун В может иметь перемещение (перемещение по горизонтали), а точка А – перемещение (отрезок перпендикулярен ОА).

Уравнение работ, выражающее принцип возможных перемещений, получает вид (1).

Найдем зависимость между возможными перемещениями точек системы. Поскольку нить, к которой привязан груз весом , нерастяжима и скольжение между нитью и валом 1 отсутствует, перемещение груза равно перемещению точки обода колеса 1. Поэтому угол поворота вала 1 и шестерни 2: .

Перемещение точки К обода колеса 2: .

Так как скольжение между шестернями 2 и 3 отсутствует, то возможные перемещения точек касания этих шестерен равны и угол поворота шестерни 3: .

Перемещение точки А кривошипа, жестко соединенного с колесом,

.

Д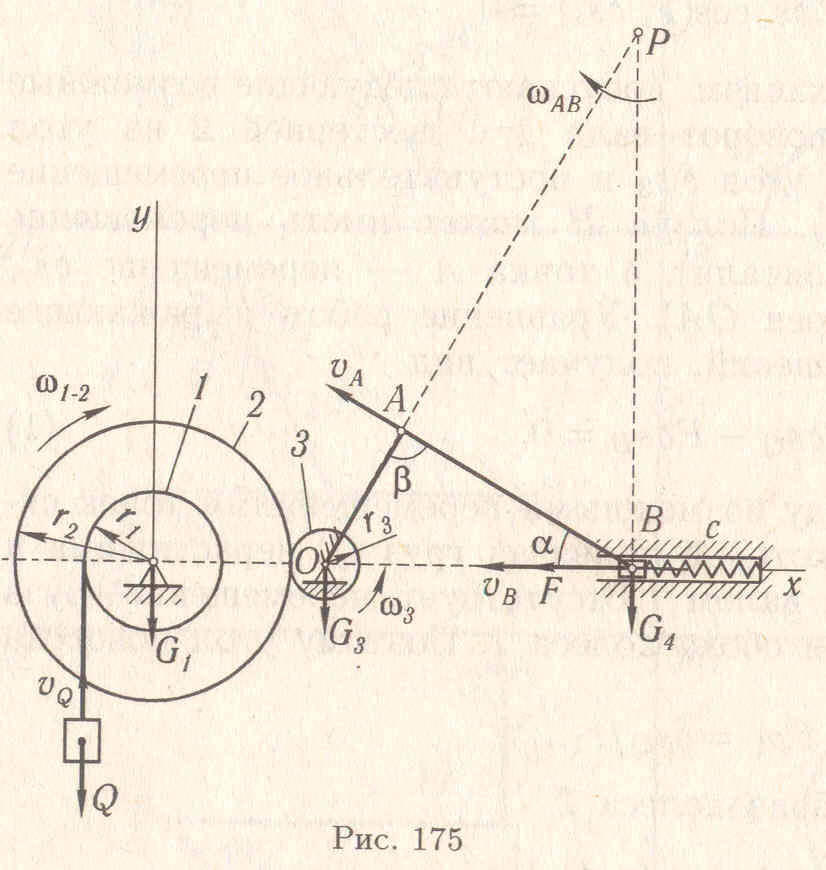 ля определения зависимости между возможными перемещениями и найдём положение мгновенного центра вращения звена АВ – точки Р: , тогда . Из получаем соотношение: .

Теперь: .

Сила упругости пружины пропорциональна её деформации: . Подставив в уравнение работ (1) выражения силы упругости и возможных перемещений точек системы, получим , откуда 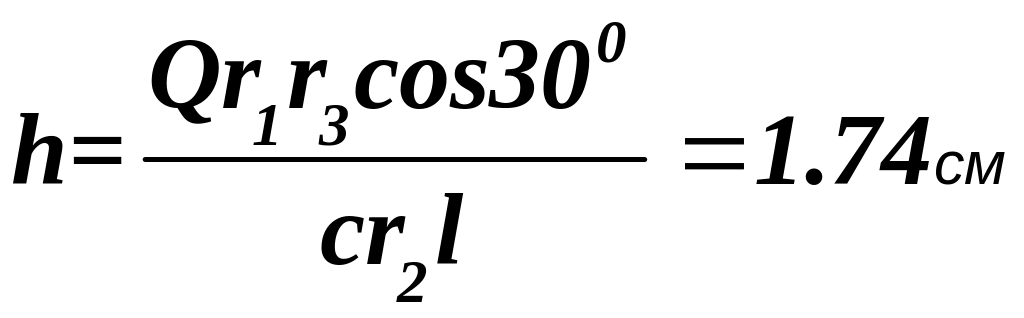. Следовательно, пружина сжата на 1,74 см.

Вариант II решения: Решим эту же задачу составлением уравнения мощностей, выражающего принцип возможных скоростей: или . Сообщим валу 1 с шестерней 2 возможную угловую скорость вокруг оси О₁, допустим, по часовой стрелке (рис. 175). Груз получит вертикальную скорость . Шестерня 3 вместе с жёстко соединённым с нею кривошипом ОА приобретает угловую скорость вокруг оси О. Звено АВ будет иметь угловую скорость , которую покажем вокруг мгновенного центра скоростей , находящегося на пересечении перпендикуляров к скоростям и точек А и В звена АВ (скорость точки А, принадлежащей кривошипу ОА, направлена перпендикулярно его направляющим). Составим уравнение мощностей: , или .

Здесь неизвестными являются деформация пружины , а также скорости и . Скорсть груза равна скорости точек обода колеса, так как нить, к которой подвешен груз, нерастяжима, и поэтому . Скорости точек касания К шестерен 2 и 3 выражаются соответственно следующим образом: и , они равны между собой так как проскальзывание в месте контакта шестерен отсутствует.

Скорость точки А можно выразить двояко, поскольку она принадлежит кривошипу ОА и звену АВ одновременно: и .

Скорость точки В звена АВ: . Таким образом, , , откуда , .

Скорость точки В: .

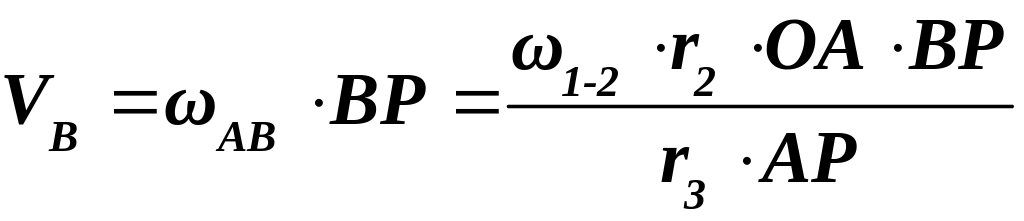Из имеем . Следовательно: .

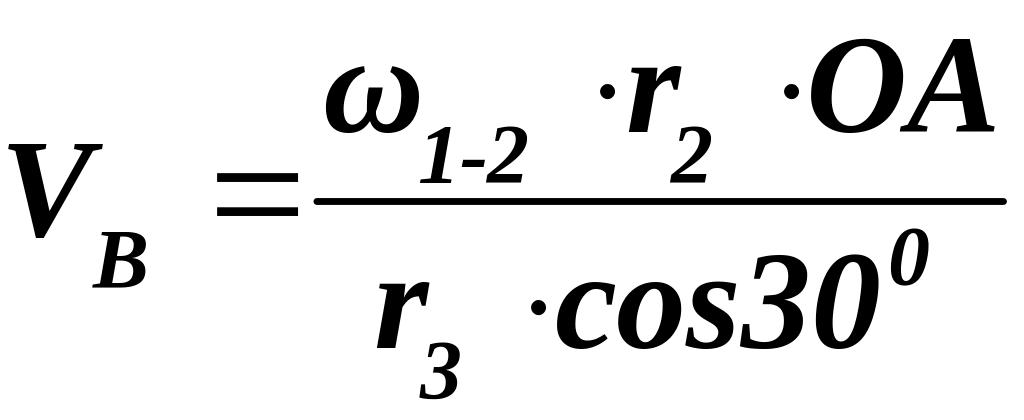Итак, уравнение мощностей приобретает вид: .

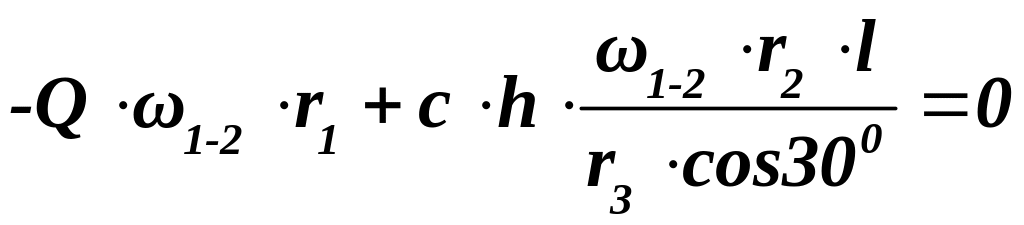Разделив все члены этого уравнения на , найдём искомую деформацию пружины:

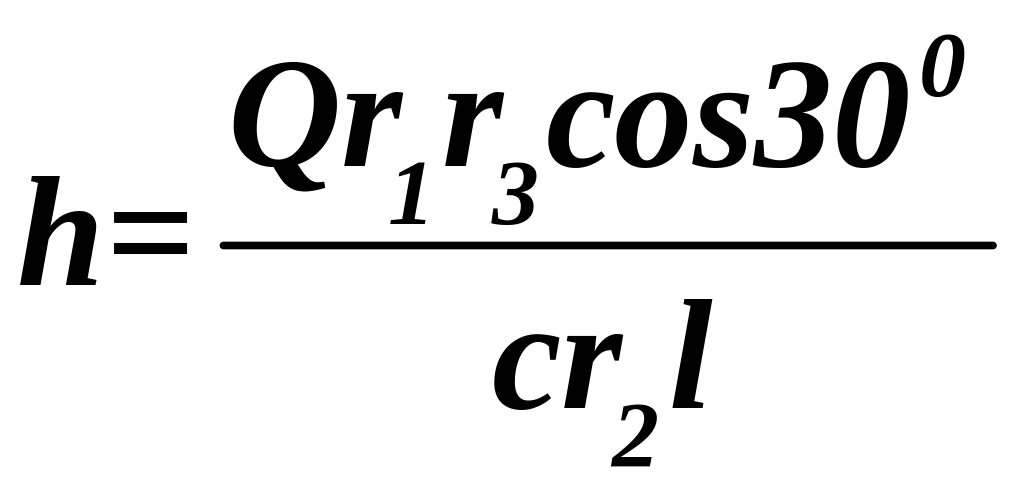. Тоесть результат совпадает с вариантом I.

-------------------------------------------------------------------------------------------------

ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ В СЛУЧАЕ ДВИЖЕНИЯ СИСТЕМЫ. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ

Если система получает возможное перемещение, при котором каждая точка имеет возможное перемещение , (рис. 253), то сумма работ этих сил на перемещении , должна быть равна нулю: (117.3)

Уравнение (117.3) называемое общим уравнением динамики, показывает, что в любой момент времени сумма работ всех задаваемых сил и сил инерции материальных точек несвободной механической системы с двусторонними идеальными связями на любом возможном ее перемещении равна нулю.

Дифференциальные уравнения движения механической системы в обобщённых координатах.