Решение:

1. Составим уравнения кинематической связи движений звеньев, выразив все движения через движение искомого тела 1.

А) перемещения: , , .

Б) скорости: , , .

В) ускорения: , , .

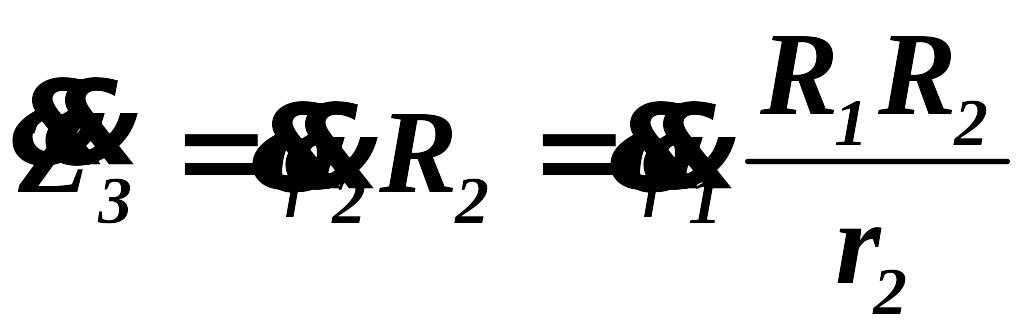2. Составим дифференциальные уравнения движения трёх звеньев.

А) звена 1 (большой диск):

Б) звена 2 (малый диск):

В) звена 3 (груз на нити):

3. У нас три неизвестных , , . Выразим их через угловое ускорение искомого звена 1 :

А) Из уравнения 2В найдём натяжение нити:

.

Б) Из уравнения 2Б , найдём окружное усилие (силу трения) между дисками №1 и №2, подставив из уравнения 3А значение натяжения нити .

и ,

В) Из уравнения 2А найдём угловое ускорение диска №1 :

мы получили дифференциальное уравнение движения второго порядка большого диска - звена №1.

4. Упростим дифференциальное уравнение 3В , подставив в него:

движущий момент ,

момент инерции диска №1 ,

момент инерции диска №2 ,

окружное усилие ,

и сведя все переменные к одной, искомой нами, переменной и времени :

Все члены с переменной (угловым ускорением диска №1) сгруппируем с одной стороны, а с переменной (время) с другой:

окончательно получим дифференциальное уравнение второго порядка вращения диска 1:

.

5. Проинтегрировав дифференциальное уравнение первый раз получим уравнение скорости (вращения) этого звена, проинтегрировав второй раз – получим уравнение движения (угла поворота) диска №1.

Уравнение скорости:

Уравнение угла поворота:

Для определения постоянных интегрирования и используем известные нам начальные условия задачи: , , .

Тогда ,

, .

Окончательно уравнение движения звена 1 примет вид:

.

Угловое ускорение диска 1 (в момент времени сек) будет равно .

Натяжение нити

Окружное усилие (сила трения между дисками 1 и 2)

.

.

Задача решена

Принцип Даламбера (метод кинетостатики)

принцип Даламбера для точки:

в произвольный момент движения материальной точки активная сила и реакция связи уравновешиваются условно приложенной силой инерции.

(22.3)

принцип Даламбера для механической системы:

если к каждой точке механической системы кроме реально действующих внешних и внутренних сил прибавить силы инерции, то полученная система сил будет уравновешенной и к ней можно применить уравнение статики.

(22.4)

(22.5)

Равенства (22.4) и (22.5) выражают условия "равновесия" внешних сил (активных и реакций связей) и условно приложенных сил инерции.

З десь - главный вектор внешних сил (активных и реакций связей).

- главный вектор сил инерции. (22.6)

- главный момент внешних сил относительно центра 0.

- главный момент сил инерции относительно центра 0.

Задача 122 (сах.)

На барабан В с неподвижной осью вращения, намотана невесомая нерастяжная нить, до конца которой прикреплен груз А весом Р₁ .Барабан В однородный сплошной цилиндр радиусом r и весом Р. Найти угловое ускорение барабана В и натяжение нити, если груз А падает. Силой трения в оси барабана можно пренебречь.

Решение:

В задаче рассматривается механическая система, состоящая из груза А и барабана В, которая движется под действием активных сил веса , и составляющих реакции неподвижной оси и .

Решим задачу с помощью принципа Даламбера, для чего к каждой массе, что находится в движении, прибавим силы инерции. Груз А движется поступательно вниз с ускорением, поэтому к нему приложим силу инерции как к точке с массой: , то есть

Вектор направлен противоположно вектору ускорения тела А .

Барабан В вращается вокруг неподвижной оси, поэтому ускорение его центра тяжести ,

а главный вектор сил инерции барабана В будет: .

Главный момент сил инерции барабана В относительно оси вращения ВХ будет:

Вектор главного момента сил инерции направлен противоположно вектору углового ускорения .

Следовательно, приложив к механической системе силы инерции, мы получили уравновешенную систему сил и моментов , которая эквивалентна 0. *)

Поэтому мы имеем право составить для нее уравнения равновесия. Запишем сумму моментов всех сил относительно оси ВХ.

- потому что эти силы пересекают ось ВХ.

; момент активной силы (вес тела А), приложенной к диску В.

; (момент силы инерции тела В отрицательный, потому что направлен противоположно вектору углового ускорения ).

Составим уравнение равновесия всех моментов, действующих на диск В, которое должно, согласно *), равняться нулю: .

Е го составляющие: .

Из этого уравнения найдём - угловое ускорение барабана В:

Для нахождения натяга нити Т рассмотрим отдельно груз А, к которому будут приложены силы, , и - реакция нити. По принципу Даламбера система сил (эквивалентная 0), а потому уравнение равновесия будет иметь обобщенный вид .

Найдём составляющие уравнения равновесия: .

Откуда сила натяга нити:

.

Задача 41.18 (41.21) Тонкий однородный стержень массой М и длиной l вращается с постоянной угловой скоростью вокруг неподвижной оси ОХ, что перпендикулярная к стержню и проходит через его конец.

Найти силу, что растягивает в поперечном сечении В стержень. Сечение В расположено на расстоянии ОВ от оси О.

Решение:

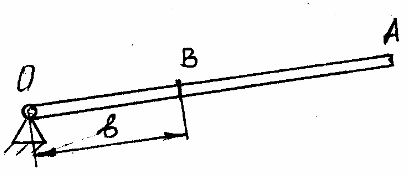
Сила , что растягивает стержень в сечении В, является внутренней силой для стержня ОА. Чтобы ее получить, разрежем стержень в точке В и рассмотрим движение правой части ВА стержня. На эту часть будет действовать сила отброшенной части ОВ, которая равна . По принципу Даламбера эта сила будет уравновешена центробежной силой инерции, то есть .

Приложим бесконечно малую силу инерции к произвольной точке К на части стержня ВА, что находится на расстоянии от оси вращения. Так как стержень ОА вращается равномерно, то касательное ускорение точки К , а нормальное и направлено к центру вращения О. Тогда бесконечно малая центробежная сила инерции, что приложена к точке К массой , будет равняться .

Бесконечно малая масса - это масса бесконечно малой части стержня длиной .

По величине она будет равна: , где - масса единицы длины стержня. Следовательно бесконечно малая сила инерции равна: .

Эта центробежная бесконечно малая сила инерции направлена всегда от центра вращения О, или противоположно . Тогда равнодействующая всех сил инерции, что нужно приложить к каждой точке части ВА стержня, будет определяться интегральной формулой:

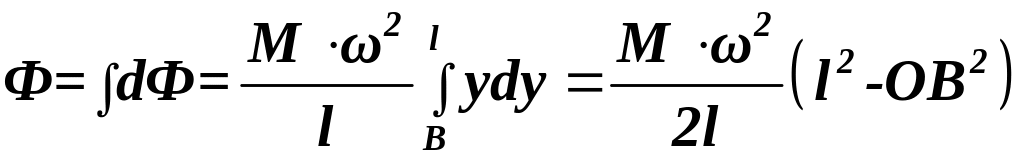
а потому сила растяжения стержня .

Максимальная сила растяжения будет при ОВ = 0, тоесть в подшипнике О, и она будет равна:

. Здесь - нормальное ускорение центра тяжести стержня.

Но согласно формулы (22.6) главный вектор сил инерции равен: .

И если нужно было бы вычислить растяжение стержня в точке О, то можно было бы обойтись и без интегрирования.

Приложение №9 б к Методическому пособию IV семестр

Метод кинетостатики (принцип Германа Эйлера Даламбера)

Пример решения задачи №61.(Яблонский стр. 281, Курс теормеха часть2)

Д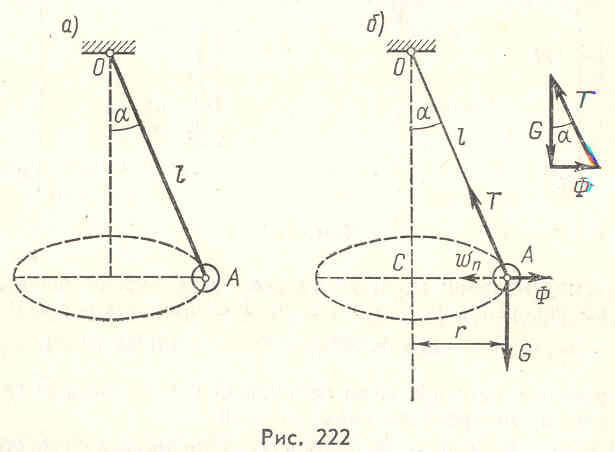 ано: Шарик А весом подвешен на нити длиной , закреплённой в неподвижной точке О. Шарику сообщено равномерное движение по окружности в горизонтальной плоскости, при котором угол наклона нити к вертикали составляет .

Определить: натяжение нити и скорость шарика этого конического маятника.

Решение: Прикладываем к шарику действующие на него силы: силу тяжести и реакцию нити . Условно приложим к шарику и его силу инерции . Так как вращение равномерное, то сила инерции состоит только с центробежной составляющей (направленной противоположно нормальному ускорению): , где . Построим замкнутый треугольник сил , , . Из этого треугольника определяем модули сил , : . . Определив модуль силы инерции, мы можем найти скорость шарика А:

.

Приложение №7а к Методическому пособию IV семестр

Тесты. Принцип возможных перемещений (Общее уравнение статики)

П ример решения задач: Дано:К кивошипу ОА приложен момент , при этом длина кривошипа . Определить: Модуль силы , приложенной к толкателю (смотри рисунок), обеспечивающей нахождение механизма в равновесии.

Покажем решение этой задачи методом статики.

Решение: Для обеспечения равновесия шатуна АВ, соединяющего кривошип ОА и ползун В, все внешние силы и реакции связей шатуна должны составить систему сил эквивалентную 0. В аналитическом виде эта система сил, приложенных к шатуну АВ будет уравновешенной при выполнении следующих условий: и .

При составлении уравнений равновесия учтём, что толкатель 1 давит на шатун АВ с силой через скользящую трубчатую насадку, т.е. усилие может передаваться от толкателя только перпендикулярно оси шатуна АВ. Учтём также, что реакция связи ползуна В направлена перпендикулярно оси рабочего хода полуна, т.е. вдоль оси . Тогда уравнения равновесия примут вид: и , где . С другой стороны от активного момента М на конце А кривошипа ОА развивается сила: . Сопоставив два последних равенства найдём .

---------------------------------------------------------------------------------------------------