Решение

Вариант№1(через потенциальную энергию П) Положение маятника будем определять двумя углами и , которые не зависят один от другого, поэтому их примем за обобщенные координаты . По этой причине маятник имеет две степени свободы ( ). На систему действуют консервативные силы - силы веса материальных точек А и В . Обобщённые силы, соответствующие двум обобщённым координатам и :

, .

Определим потенциальную энергию системы П, которая будет равняться сумме работ сил при переходе системы из данного положения в нижнее вертикальное, когда :

, ,

.

Тогда обобщенные силы этой консервативной системы:

,

.

Вариант №2 (через работу обобщённой силы) Этот же ответ можно получить, если вычислить элементарную работу по формуле: .

Для этого запишем координаты точек Аи В в декартовой системе через обобщенные координаты.

Так как и , то нужны только координаты и :

и

Сообщим бесконечно малый прирост углу , а угол прироста иметь не будет, то есть .

Тогда .

Вычислим на этом перемещении сумму элементарных работ сил притяжения .

, .

Тогда первая обобщенная сила равняется: .

Аналогично сообщим бесконечно малое перемещение углу , считая, что .

Тогда , , ,

, тогда: .

Результаты для первой и второй обобщенных сил совпадают с вариантом №1.

Методика решения задач с помощью уравнений Лагранжа II рода

Для того, чтобы составить уравнение Лагранжа, нужно:

1. Выбрать обобщенные координаты.

2. Приложить к механической системе действующие на нее активные силы.

3. Сообщить бесконечно малое приращение одной из обобщенных координат, например , и при этом считать, что другие координаты такого прироста не имеют, тоесть: . На приросте вычислить сумму элементарных работ активных сил и разделить ее на , то есть вычислить обобщенную силу , что отвечает координате . (см. 27.4)

4. Вычислить Т - кинетическую энергию системы в ее абсолютном движении.

5. Взять соответствующие частные производные от Т по , и составить соответствующие уравнения (30.3).

6. Интегрируя составленные дифференциальные уравнения и используя начальные условия, получить уравнение движения системы в виде , ,…, .

Пример, 48.35. (48.37). Составить уравнение движения эллиптического маятника, который состоит из ползуна А массой , шара В массой и невесомого стержня АВ длиной , что соединяет ползун А и шар В. Стержень может вращаться вокруг оси А, перпендикулярной к плоскости рисунка. Ползун двигается без трения.

Вычислить период малых колебаний маятника.

Р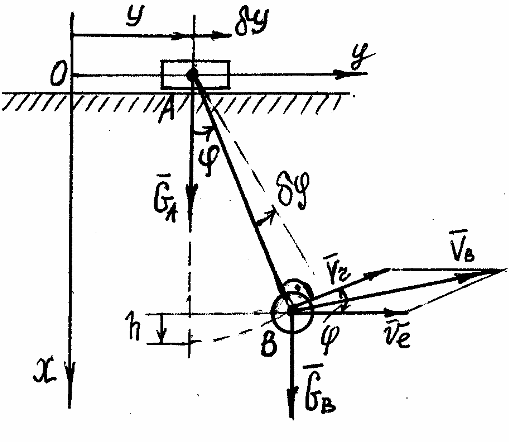 ешение:

Положение ползуна определяется координатой , а стержня АВ - углом вращения , которые между собой не связаны. Следовательно, обобщенных координат две: , , а поэтому система имеет две степени свободы S=2 и нужно составить два дифференциальных уравнения. Уравнения Лагранжадля этих двух обобщённых координат имеют вид:

*), **)

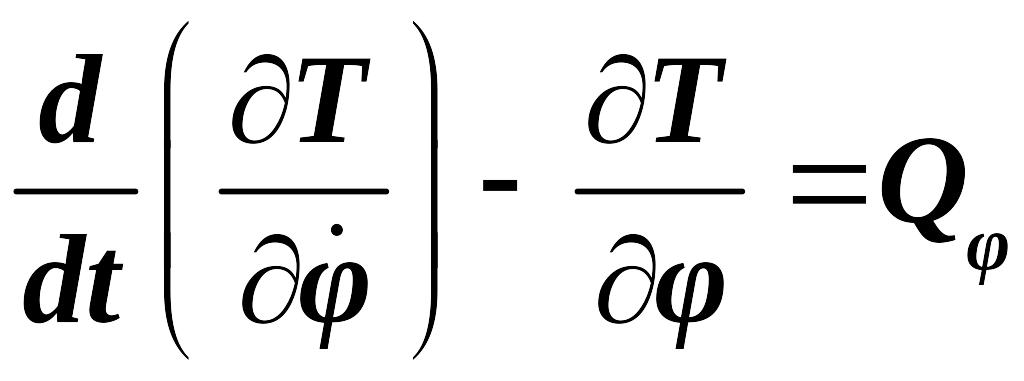На систему с идеальной связью (поверхность гладкая) действуют силы веса , и реакция опоры (связь) . Для вычисления обобщенной силы дадим бесконечно малый прирост координаты , а угол прироста не будет иметь ( ). Вычислим элементарную работу сил и : , потому что эти силы перпендикулярные .

Тогда - это правая часть уравнения *).

Теперь дадим бесконечно малый прирост углу , при этом считаем, что , то есть ползун не двигается. Тогда элементарная работа будет:

, .

Тогда - это будет правая часть уравнения **).

Обобщенную силу можно вычислить иначе. На систему действуют потенциальные силы - силы притяжения и . Поэтому обобщенную силу можно вычислить по формуле (27.6)

Вычислим потенциальную энергию системы

, где , поэтому потенциальная энергия - равна работе силы при переходе шара В из положения в положение .

Найдем и .

Вычислим кинетическую энергию ползуна А и шара В

- ползун движется поступательно.

Шар В выполняет сложное движение.

Относительное движение - это вращение вокруг оси А с угловой скоростью , поэтому и . Переносное движение - это поступательное движение ползуна А со скоростью , следовательно переносная скорость , а вектор (направленный параллельно оси ОY).

Тогда абсолютная скорость шара В будет

А кинетическая энергия шара В:

Как видим, здесь кинетическая энергия зависит не только от обобщенных скоростей и , но и

от обобщенной координаты .

Кинетическая энергия всей системы: .

Берем соответствующие частные и полную производную по t от кинетической энергии системы:

, потому что в выражение кинетической энергии не входит координата .

Тогда первое дифференциальное уравнение будет иметь вид: (*1)

, , .

Подставляем производные и обощённую силу в уравнение **)

Тогда второе дифференциальное уравнение будет иметь конечный вид:

(**2)

Таким образом, мы составили систему дифференциальных уравнений движения данной механической системы - эллиптического маятника.

Для вычисления периода малых колебаний маятника положим в уравнениях (*1) и (**2) упрощения тригонометрических функций: , :

из этих уравнений исключаем , для чего во втором уравнении

выделим : , и подставим это выражение в первое уравнение, получим:

Упростим это линейное дифференциальное уравнение:

Обозначим константу дроби перед через : .

Тогда . Мы получили дифференциальное уравнение малых колебаний эллиптического маятника, где - циклическая или круговая частота колебаний маятника.

Период колебаний маятника .

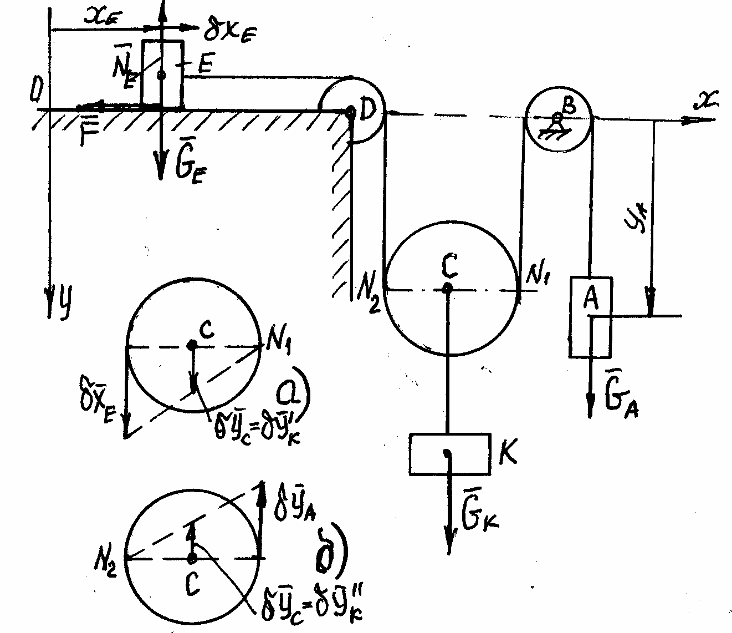
Пример 48.26. (47.20).

Однородная нерастяжимая нить, до конца которой привязан груз А массой , переброшена через два неподвижных блока В и D и подвижный блок С и проходит параллельно горизонтальной плоскости, где к ее концу привязан груз Е массой . К оси С подвижного блока прикреплен груз К массой . Коэффициент трения скольжения груза Е равняется . При каком условии груз К будет опускаться, если начальная скорость всей системы равнялась нулю? Найти ускорение груза К, пренебрегая массами нити и блоков. Решение.

Возьмем неподвижную систему координат хОу, как показано на рисунке. Положения данной системы будут определять две независимые координаты и . Тогда они будут обобщенными координатами и , а уравнения Лагранжа будут иметь вид:

На систему действуют силы тяжести , , , , сила трения и реакция .

Для вычисления обобщенной силы , что отвечает обобщенной координате , дадим последней бесконечно малое приращение . При этом будем считать, что груз А не двигается, то есть . Тогда все точки нити от А к N₁ не будут двигаться, поэтому , а ( смотри рис. а)).

Элементарная работа на перемещении будет:

.

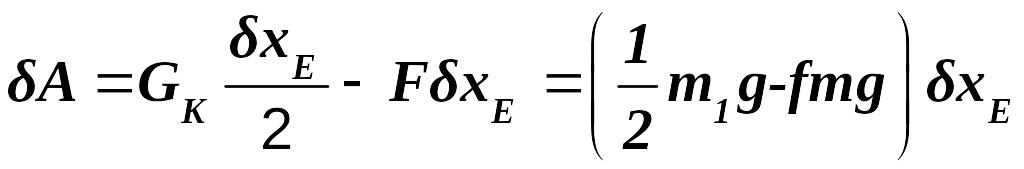потому, что и .

потому, что .

Следовательно .

Для вычисления обобщенной силы ,соответствующей координате , дадим последней приращение . При этом будем считать, что груз Е не двигается, то есть .

Тогда все точки нити от Е к N₂ будут иметь скорость, ровную нулю, а потому (смотри рис. б) ). Вычислим элементарную работу на перемещении :

потому что .

, .

Тогда , а .

Зависимость между бесконечно малыми перемещениями , , можно получить иначе. Нить не растягивается, поэтому длина всех ее частей будет неизменной при движении системы.

То есть

Продиференцируем (или возьмем вариации) это равенство, где и тоже постоянные величины. Тогда

Но , поэтому . Если взять производную по t, то получим зависимость между обобщенными скоростями: *)

и ускорениями: . *)

Тогда при и ,

при и .

Скорость и ускорение координаты равняются (смотри *)):

и .

Вычислим кинетическую энергию системы:

Грузы двигаются поступательно, со скоростями: , , .

Поэтому: .

Берем соответствующие частные и полную производную по t: , , и по скоростям: , .

Дифференциальные уравнения движения системы:

, .

Найдем разницу этих уравнений:

Учитывая, что , имеем:

Тогда .

Для того, чтобы груз К опускался, нужно чтобы выполнялось неравенство ,

то есть , или .

Конец

-------------------------------------------------------------------------

Контрольное Задание Д-23.

Пример решения задачи по исследованию свободных колебаний механической системы с одной степенью свободы с использованием уравнения Лагранжа II рода для консервативной системы.

Дано: , , , , , , , .

Определить: циклическую частоту и период малых свободных колебаний системы, а также получить уравнение колебаний груза 1 и найти амплитуду его колебаний.