Министерство образования и науки Украины

Национальный университет кораблестроения

имени адмирала Макарова

Феодосийский политехнический институт

Теоретическая механика

Методическое пособие

«Динамика механической системы и

основы аналитической механики»

Феодосия

Приморский

2010г

Методика содержит следующие разделы:

I. Динамика механической системы

II. Основы аналитической механики

Каждый раздел содержит две главы:

1. Примеры решения типовых расчетно-графических задач и контрольных работ.

2. Примеры решения контрольных работ Д-10, Д-11, Д-14, Д-19, Д-23.

В Приложении даны: ТЕСТЫ - Перечни РГЗ, Контрольные задания, подлежащие решению на практических занятиях и СРС. (см отдельный файл)

Раздел I Динамика механической системы

Примеры решения типовых расчётно-графических задач по разделу моменты инерции твёрдого тела:

Теорема Штейнера - Гюйгенса.

Момент инерции твердого тела относительно оси, параллельной центральной, равняется сумме момента инерции относительно центральной оси и произведения массы тела на квадрат расстояния между осями.

Пример 34.21

Маятник состоит из тонкого однородного стержня АВ массой m₁, к которому прикреплен однородный диск Д массой m₂ и радиусом r. Вычислить момент инерции маятника относительно оси Ох, перпендикулярной к плоскости маятника АВ=4r, АО=r.

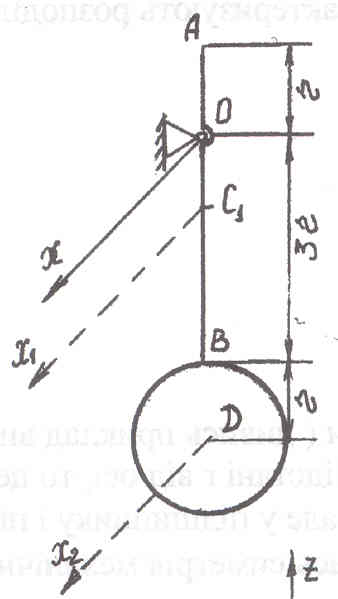
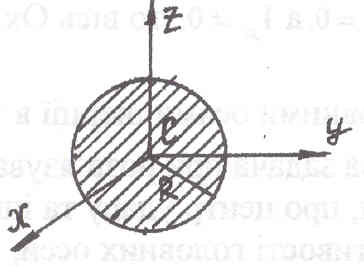
Решение:

В справочниках и лекциях можно найти формулы моментов инерции тонкого стержня относительно центральных осей:

, а также однородного диска: ,

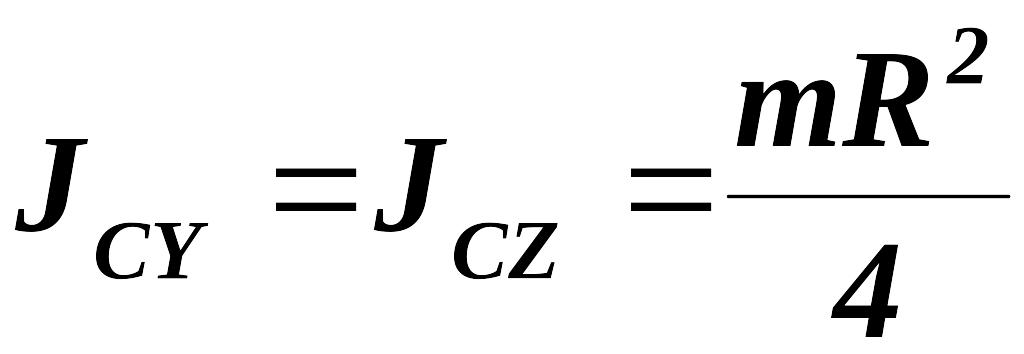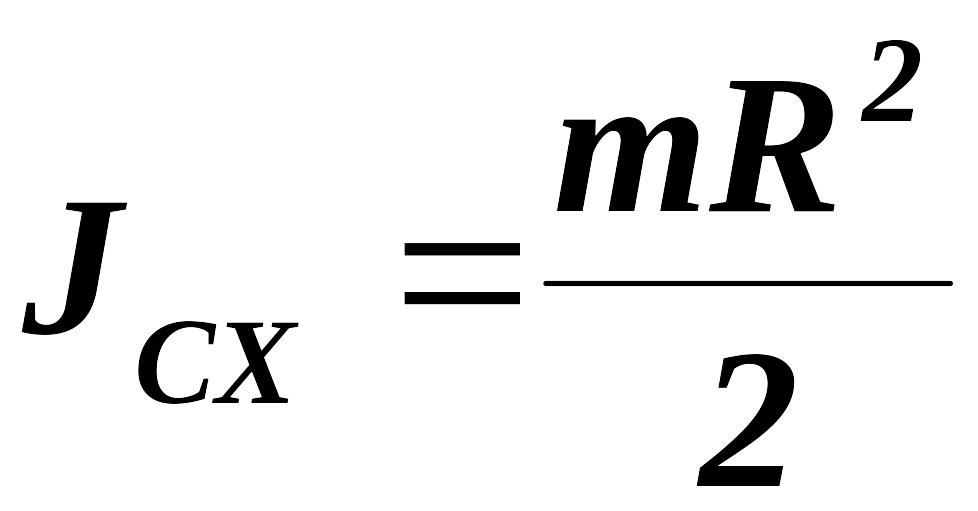
Следовательно, используя эти формулы и (3.13), запишем момент инерции стержня АВ относительно оси Ох:

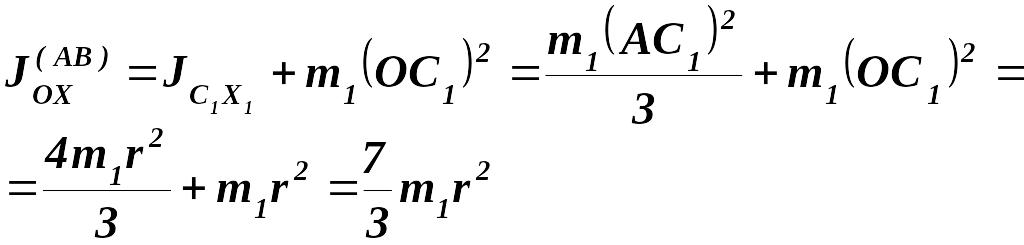
где - масса стержня АВ, и - радиус диска.

Момент инерции диска Д относительно оси Ох, согласно с (3.13):

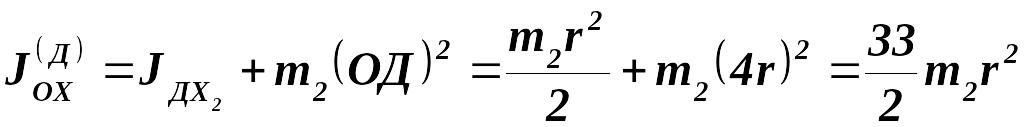
где - масса диска. Тогда момент инерции всьго маятника будет:

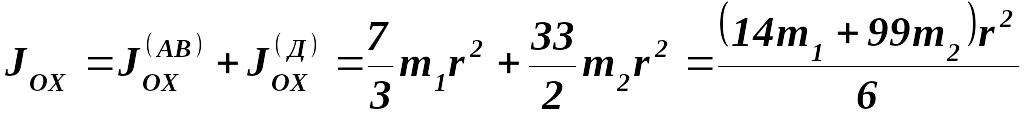
Пример 34.31(34.34) Вращающаяся часть подъемного крана состоит из стрелы СД = L массой , противовесы массой и груз K массой . Считая стрелу однородной тонкой балкой, а грузы Е и K материальными точками, определить момент инерции крана относительно оси вращения Z и центробежные моменты инерции относительно осей X,Y,Z которые связаны с краном. Центр тяжести С всей системы находится на оси Z, а ZAY - плоскость симметрии, в которой находится стрела.

Р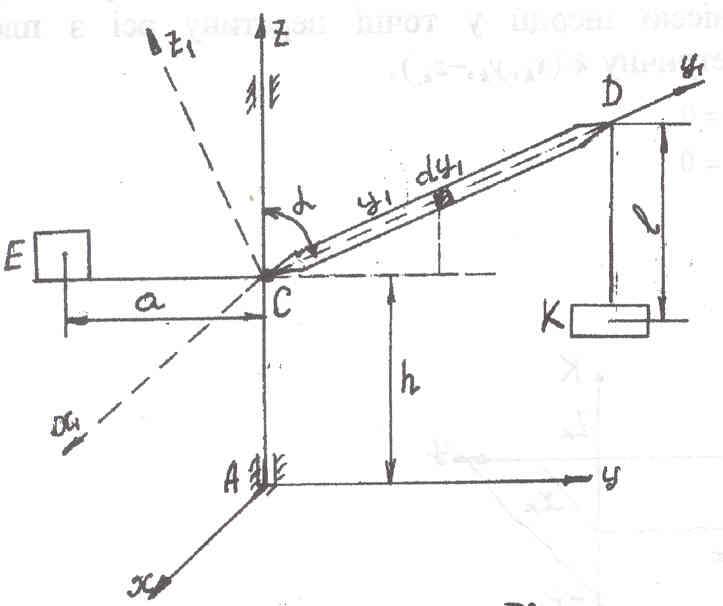 ешение

-момент инерции всей системы крана и груза. Моменты инерции составных элементов системы:

Противовесы: ,

Груза: ,

Для балки (однородный тонкий стержень) СД известны моменты инерции относительно осей CX₁,CY₁,CZ₁. и . Но эти оси параллельные центральным, поэтому они главные, тогда центробежные моменты инерции . Тогда за формулой (5.2) можно записать

Где

Следовательно: .

А для всей системы момент инерции будет:

ZАУ - плоскость симметрии, поэтому ось АХ - главная ось инерции, поэтому .

Обчислемо центробежный момент инерции : .

Моменты инерции для противовеса Е, и груза К:

,

Для стрелы СД запишем центробежный момент элемента массой , тогда

Момент инерции стрелы по всей ее длине:

Для всей механической системы:

Найдем координату центра веса системы

потому что центр тяжести системы за условием задачи находится на оси Z (это является условием равновесия крану при поднятии груза). Следовательно центробежный момент инерции системы равняется:

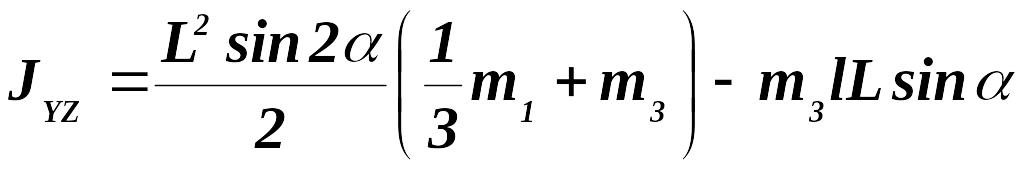
Расчётно-графические задачи, показанные в приложении №1 к настоящему «Методическому пособию», предлагается решать студентам самостоятельно в рамках содержательного модуля СМ4.3.2. При этом формулы моментов инерции типовых фигур и теорема Штейнера указаны в теоретической части настоящего МП и в курсе лекций.

Примеры решения типовых расчетно-графических задач и контрольных работ раздела динамика механической системы

Теорема 1. (о движении центра масс.)

Для механической системы имеем второй закон Ньютона для центра масс: (7.1) Следовательно имеем теорему:

Центр масс механической системы двигается как точка, что имеет массу всей системы, под действием внешних сил, которые действуют на механическую систему.

В проекциях на декартовы оси имеем: (7.2)

- главный вектор внешних сил, а - проекции главного вектора внешних сил на оси декартовы координат.

С помощью этой теоремы можно изучать поступательное движение механической системы, потому что в поступательном движении все точки имеют одинаковые скорости и ускорения. Как и в динамике точки, можно рассматривать прямую и обратную задачи.

То есть, если задано движение центра масс, то можно найти ускорение центра масс, а потому и главный вектор внешних сил, или одну из неизвестных сил.

Если же внешние силы будут известны, то нужно составить дифференциальные уравнения в виде (7.1), а затем (7.2) и развязав их, найти уравнение движения центра масс.

Закон сохранения центра масс в координатном виде: (8.3)

Пример 35.19.

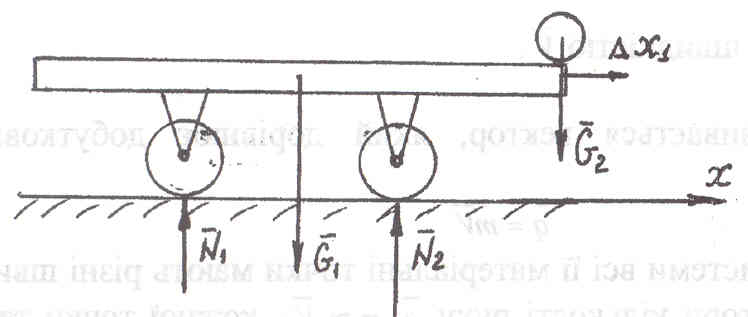
По горизонтальной грузовой платформе длиной 6м и весом 2700 кг, которая в начальный момент не двигалась, двое рабочих перекатывают тяжелую стальную отливку с левого конца платформы в правый. В какую сторону и на сколько переместится при этом платформа, если общий вес отливки и рабочих 1800 кг? Силы сопротивления движения платформы не учитывать.

Решение.

На механическую систему „платформа + отливка + рабочие" действуют внешние силы: -веса платформы, - веса отливки и рабочих, и - реакции нормального давления на колею первой и второй пары колес.

Направим ось Х вправо и спроектируем внешние силы на нее .

В момент платформа с грузом не двигалась и . А потому .

Используем закон сохранения центра масс в виде (8.3)

, или

Здесь - перемещение платформы по оси Ох возьмем вправо, то есть . - абсолютное перемещение рабочих и отливки, которое состоит из переносного

и относительного . Следовательно .

Тогда , откуда .

Знак "-" указывает на то, что платформа будет двигаться противоположно передвижению отливки.

Количество движения механической системы:

Количеством движения точки называется вектор, который равняется произведению и направленный как вектор _:

О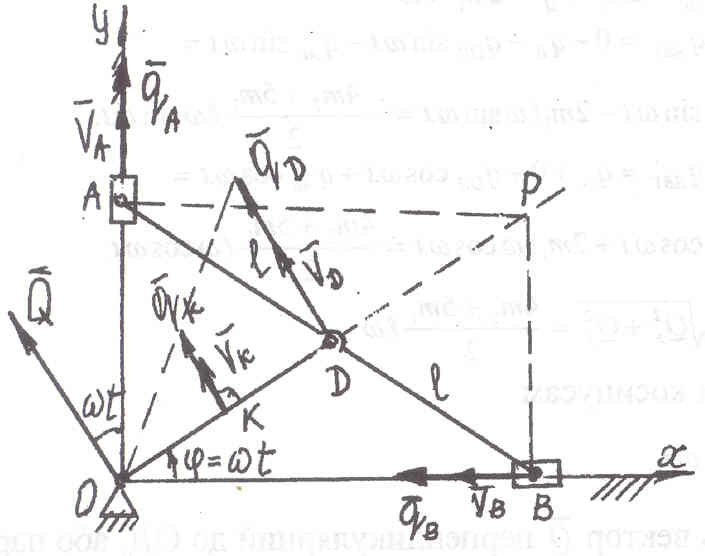 пределение вектора количества движения механической системы через скорость ее центра масс: . Направление вектора будет такое же, как и .

Вектор можно приложить в любой точке механической системы, тогда он будет называться главным вектором количества движения.

Пример 36.4.

Определить величину и направление главного вектора количества движения механизма элипсографа, если масса кривошипа , масса линейки , масса каждой из муфт А и В равняется . ОД=АД-ВД=l.

Центры тяжести кривошипа и линейки расположены в их серединах. Кривошип вращается с постоянной угловой скоростью .

Развяжем задачу первым способом.

Найдем скорости точек приложения масс, то есть (К - середина ОД). Кривошип ОД вращается вокруг оси О с угловой скоростью . Тогда , где и ,

где . Муфты А и В двигаются по осям координат, поэтому , направлена по ОY, а , направлена по ОХ. Тогда мгновенный центр скоростей линейки АВ будет в точке Р на пересечении перпендикуляров к и . Из пропорции получим скорость муфты А:

Анологично найдем : , тогда

Тогда количества движений муфт, кривошипа и линейки будут:

Проекции на оси координат главного вектора количества движения механизма элипсографа:

Тогда модуль главного вектора количества движения механизма элипсографа равняется:

Его направление найдем по направляющим косинусам:

и .

Такое соотношение косинусов означает, что вектор перпендикулярный к ОD, или параллельный векторам количества движения и .

Развяжем задачу вторым способом, для чего вычислим координаты центра масс системы:

где Подставим эти значения координат центров масс составляющих системы и найдем координаты центра масс системы в целом:

Найдем первый дифференциал координат центра масс системы, тоесть определим скорость коодинаты центра масс системы: , тогда модуль скорости центра масс системы: .

Определим модуль главного вектора количества движения системы:

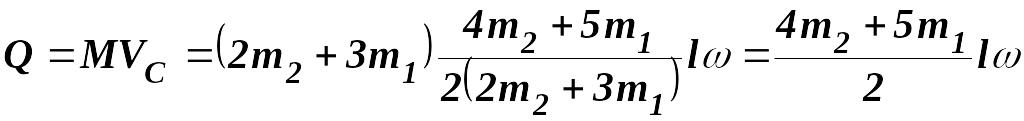
Проекции на декартовые оси модуля главного вектора количества движения системы:

Направляющие косинусы главного вектора количества движения системы:

,

В приложении №2 к настоящему МП даны билеты тест-контроля по изменению количества движения. Оценка решения РГЗ по этим билетам осуществляется в рамках СРС и содержательного модуля СМ4.3.2.

-----------------------------------------------

Методика развязывания задач с помощью теоремы об изменении момента количества движения механической системы (кинетического момента)

1.К механической системе приложить внешние силы.

2.Вычислить сумму моментов внешних сил относительно оси вращения . Это будет правая часть дифференциального уравнения, которое нужно составить по условию задачи.

3.Вычислить кинетический момент механической системы

4.Производную по времени от кинетического момента приравнять к выражению, что получим в п.2

5.Развязать полученное дифференциальное уравнение, используя известные начальные условия.

Пример: 37.43 (37.42)

При приведении к движению электрической лебедушки, к барабану А прилагаемый вращающий момент, пропорциональный времени , - постоянный коэффициент.

Р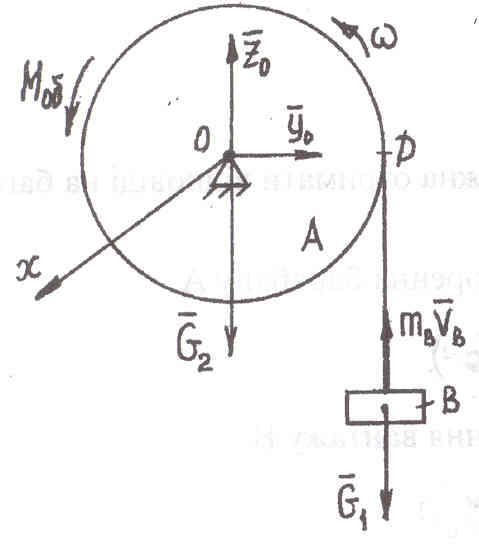 ешение:

Для определения угловой скорости барабана А используем теорему об изменении кинетического момента:

1.К барабану А приложим вращающий момент, силу притяжения барабана, составляющие реакции оси барабана, а к грузу В силу притяжения .

2.Найдем сумму моментов всех сил относительно оси ОХ:

потому что сила пересекает ось ОХ.

3.Вычислим кинетический момент данной механической системы .

Барабан А вращается вокруг оси ОХ, поэтому .

Груз В двигается поступательно со скоростью и имеет количество движения, направленное как .

Кинетический момент груза: .

Кинетический момент системы тел А и В: .

4. Возьмем производную и приравняем к сумме моментов сил относительно оси ОХ:

. *)

Мы получили дифференциальное уравнение движения механической системы „груз-лебёдка”. Разделим в нем переменные и проинтегрируем полученное уравнение: .

Получим **)

Подставим известные нам начальные условия и найдем коєффициент интегрирования С₁:

При , тогда

и . Тогда **) будет иметь конечный вид: .

Найдем [cек^-1]. ***)

Замечание: из дифференциального уравнения можно получить ответы на многие вопросы:

1. Так как, то можно найти угловое ускорение барабана А: .

2. Так как , то можно найти ускорение груза В: .

3. Подставив в ***) получим дифференциальное уравнение, из которого найдем закон вращения барабана А: .

Проинтегрируем это уравнение: , выйдем

из под знака интегралов:

Определим постоянную интегрирования С, подставив в последнее уравнение начальные значения времени и угла поворота: , , тогда: , откуда .

Закон вращения барабана А получит окончательный вид:

[радиан].

4. Произведение - есть закон движения груза В, в вертикальном направлении.

То есть: [м].

-----------------------------------------------------------

Кинетическая энергия механической системы

Кинетическая энергия - это мера механического движения, которая характеризует способность механического движения превращаться в эквивалентное количество иного движения

Кинетическая энергия механической системы равняется арифметической сумме кинетических энергий точек, с каких складывается механическая система

. Поэтому (16.7), где - это кинетическая энергия системы в движении по отношению к центру масс механической системы, а так как центр масс системы, точка С, размещена нами в начале подвижной системы координат, то эту составляющую можно также назвать кинетической энергией относительного (вращательного) движения механической системы.

Таким образом кинетическая энергия механической системы равняется сумме кинетической энергии центра масс системы (что двигается поступательно), масса которого равняется массе всей системы, и кинетической энергии этой системы в ее относительном движении по отношению к центру масс. Равенство (16.7) и есть теорема Кьонига.

Рассмотрим примеры решения двух РГЗ входящих в Приложение 3 к настоящему Методическому пособию и определим кинетическую энергию механической системы

РГЗ №2

Дано: угловая скорость кривошипа1 , массы деталей момент инерции спаренного диска (деталь 2) , радиусы дисков .

Определить: кинетическую энергию механической системы.

Решение:

1.Кинетическая энергия системы состоит из суммы кинетических энергий звеньев системы:

2.Найдём кинетическую энергию кривошипа ОА, как стержня с осью вращения на конце О: , где момент инерции стержня: и , тогда: .

3.Найдём кинетическую энергию диска 2, движущегося плоско-паралельно. Т диска состоит из вращательной составляющей (вращение диска вокруг точки А) и поступательной составляющей (поступательное движение центра тяжести диска точки А). , где , раскроем обе составляющие кинетической энергии: и . Тогда: .

4.Кинетическая энергия неподвижного диска 3 равна 0: .

5.Суммарная кинетическая энергия механизма: .

6.Проверка Т₂: Рассмотрим движение диска 2 не как плоско-параллельное, а как абсолютное вращение вокруг его неподвижного МЦС - точки Р₂.

Тогда кинетическая энергия диска определяется с помощью теоремы Штейнера: , и кинетическая энергия равна: . Как видим результат совпал с п.3.

Рассмотрим ещё одну расчётно-графическую задачу из приложения №3 к МП.

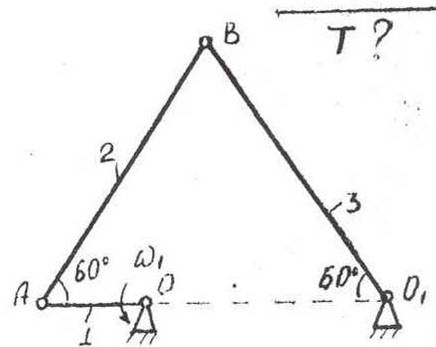РГЗ №18

Дано: угловая скорость звена ОА , его длина , массы звеньев: , .

Определить: Т всей системы.

Решение:

1. Суммарная кинетическая энергия системы:

2. Звено 1 – стержень закреплённый шарнирно на конце тч О. Поэтому его кинетическая энергия равна: , где момент инерции стержня относительно тч О равен . Тогда .

3. Найдём кинетическую энергию звена 2. Звено 2 вращается вокруг своего мгновенного центра скоростей Р₂, совпадающего с точкой О₁. (это видно из направлений скоростей точек А и В этого звена). Найдём угловую скорость вращения звена 2: , тогда: .

Кинетическая энергия: , где, согласно теореме Штейнера, момент инерции звена 2 относительно тч О₁: . Расстояние от центра тяжести звена 2 (это середина звена 2) равно: . Момент инерции относительно центра тяжести: . Тогда .

Кинетическая энергия звена 2: .

4. Звено 3 вращается вокруг точки О₁ поэтому . Момент инерции стержня ВО₁ равняется . Угловая скорость звена 3, вращающегося вокруг своего МЦС, точки О₁, равняется: . Тогда момент инерции . Кинетическая энергия звена 3: .

5. Кинетическая энергия всей механической системы:

Р асчётно-графические задачи приложения №3 к МП должны решаться студентами в рамках выполнения содержательного модуля СМ4.3.2. – самостоятельная работа студентов

Задача 38.5 (38.5) (задачи из курса лекций Кузнецовой - НУК)

Определить кинетическую энергию кривошипно-шатунного механизма, если масса кривошипа , длина ОА= r, масса ползуна , длина шатуна АВ = l. Масой шатуна пренебречь. Кривошип считать однородным стержнем. Угловая скорость кривошипа равняется ω.

Решение:

Кинетическая энергия всего механизма будет:

Кривошип вращается вокруг неподвижной оси О, поэтому:

Ползун В двигается поступательно по оси Х: .

Запишем уравнение движения ползуна В:

Скорость ползуна В будет: .

Тогда .

А кинетическая энергия всего механизма будет: .

Задача 38.6 (38.6)

Развязать задачу 38.5 для положения механизма, когда кривошип ОА будет перпендикулярным к направляющей ползуна (к линии движения ползуна). При этом масса шатуна будет

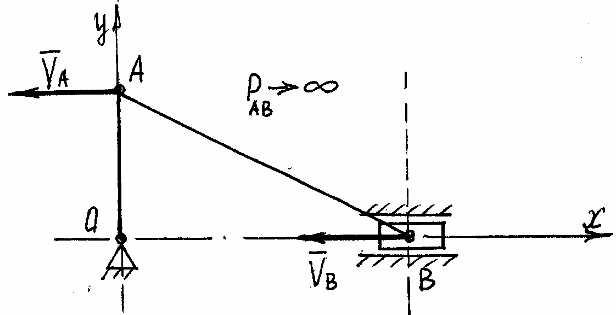Решение:

В этом случае мгновенный центр скоростей шатуна АВ (МЦС), точка Р_АВ будет в бесконечности, а поэтому и шатун АВ в этот момент будет двигаться поступательно. Тогда скорости всех его точек будут ровными по величине и направлению, то есть: . Формула кинетической энергии всего механизма в этом случае трансформируется в сумму:

И каждая ее составляющая будет равняться:

следовательно .

Задача 38.7

Планетарный механизм, расположенный в горизонтальной плоскости, приводится в движение кривошипом ОА, на котором находятся оси трех одинакових колес (дисков) радиусом . Масса каждого колеса , масса кривошипа ОА . Вычислить кинетическую энергию механизма, если колеса являются однородными дисками, а кривошип – однородный стержень. Первое колесо – неподвижное.

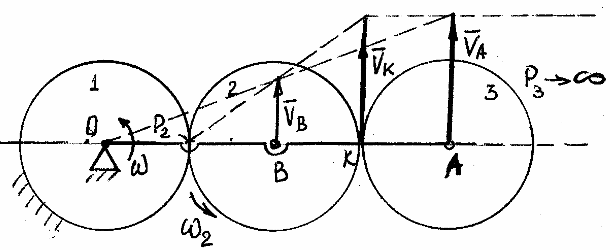
Решение:

Кинетическая энергия механизма будет:

Кривошип ОА вращается вокруг неподвижной оси О,

поэтому :

Колесо 2 осуществляет плоско-параллельное движение, или мгновенный поворот вокруг его мгновенного центра скорости (МЦС) тч Р₂ (это точка касания диска 2 к неподвижному диску 1, поэтому ее скорость ). Тогда, согласно формулы кинетической энергии для вращательного движения:

где , , откуда . С учетом этих превращений, кинетическая энергия диска 2: .

Точка А на колесе 3 будет иметь скорость: .

Точка К прикосновения колеса 3 к колесу 2 будет иметь скорость:

Обе скорости направлены перпендикулярно ОА в одну сторону и равны по модулю. Следовательно МЦС колеса 3 тч Р₃ будет в бесконечности и угловая скорость диска 3 будет равняться нулю:

Это означает, что колесо 3 осуществляет поступательное движение со скоростью , поэтому кинетическая энергия диска 3:

Кинетическая энергия всего механизма будет: .

------------------------------------------------------------------------

Определение работы звеньев механической системы

(Приложение 4 к Методическому пособию IV семестр)

Р ГЗ №2. Дано: Диск радиусом и весом катится по наклонной плоскости. Длина пути . На диск действует момент сопротивления качению и сила трения . Найти: работу всех сил

Решение:

1. Работа всех сил равна .

2. Работа силы веса зависит только от перепада высот: .

3. Работа момента сопротивления качению: , где угол поворота диска на пути S: [рад].

Момент сопротивления качению: .

Тогда работа этого момента .

4. Работа силы трения скольжения: , так как нет проскальзывания – значит и нет работы силы трения (в точке контакта диска с наклонной поверхностью расположен МЦС диска).

5. Суммарная работа всех сил: .

Р ГЗ №14. Дано: Крутящий момент поворачивает из горизонтального положения на прямой угол 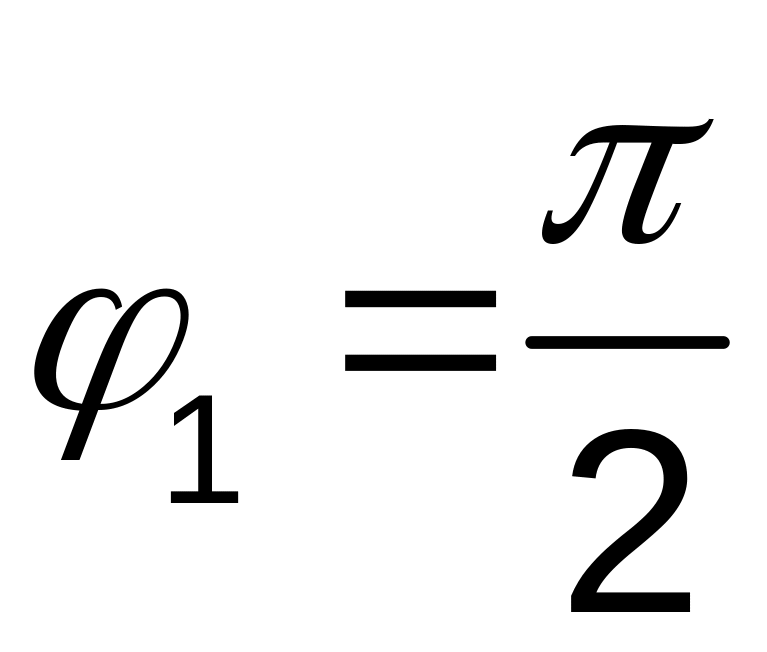кривошип . Известно также что: , , , . Определить: кинетическую энергию всей системы.

Решение:

1. Суммарная работа всех внешних сил, воздействующих на систему: .

2. Работа крутящего момента: .

3. Работа силы тяжести: (направление движения противоположно направлению вектора силы тяжести, т.е. cos180⁰=-1).

4. Работа силы тяжести: . (высота перемещения центра тяжести звеньев 1 и 2 одинаковая ).

5. Работа силы тяжести: т.к. ползун 3 движется горизонтально без силы трения.

6. Суммарная работа всех внешних сил, воздействующих на систему:

.

--------------------------------------------------------

Теорема об изменении кинетической энергии материальной точки и механической системы

Теорема об изменении кинетической энергии точки в конечной, или интегральной форме:

Мощность равняется производной по времени t от кинетической энергии точки:

Теорема об изменении кинетической энергии механической системы в конечной форме:

Изменение кинетической энергии на конечном перемещении равняется сумме работ внешних и внутренних сил на этом же перемещении:

Пример 38.24 (из курса лекци й Кузнецовой - НУК)

Н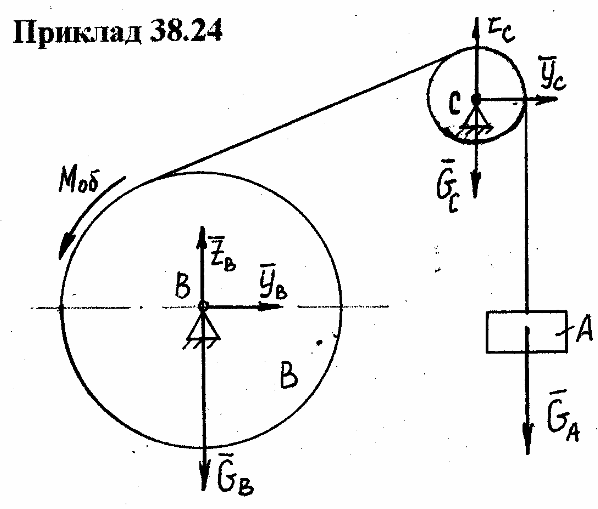 а рисунке изображён подъёмный механизм лебёдки. Груз А массой m₁ поднимается тросом, который перекинут через блок С и намотан на барабан В радиуса r и массой m_2. К барабану В приложен вращательный момент М_об, который с начала движения пропорционален квадрату угла вращения барабана: , где - постоянный коеффициент.

Определить скорость груза А в момент, когда он поднимется на высоту h. Массу барабана В считать равномерно распределенной по ободу, а блок С массой m₃ – сплошным однородным диском. Массой троса можно пренебречь. Система приводится в движение из начального состояния покоя.

Решение: К механической системе приложены силы веса, реакции неподвижных шарниров, и вращательный момент . По теореме об изменении кинетической энергии механической системы запишем: , где

- стартовая кинетическая энергия системы, находящейся в состоянии покоя.

- кинетическая энергия системы в тот момент, когда груз А поднимается на высоту h.

Она будет равняться арифметической сумме кинетических энергий всех частей системы

.

Груз А движется поступательно, поэтому .

Блок С и барабан В вращаются вокруг неподвижных осей, поэтому:

,

.

Следовательно, полная кинетическая энергия системы .

Внутренние силы – это силы взаимодействия между грузом А и блоком С, между барабаном В и блоком С. Это силы натяжения троса на звеньях АС и ВС. Они равны между собой и противоположно направленные, а точки их приложения имеют одинаковую скорость и одинаковое перемещение, а значит трос не растягивается. Поэтому .

Работы внешних сил на перемещении составляющих А, В, С механической системы:

,

Но , так как они приложены к неподвижным точкам. Работа силы веса груза А, движущегося вверх:

Известно, что элементарная работа вращательного момента

Тогда работа вращательного момента на конечном повороте, когда , будет:

.

Следовательно, работа всех внешних сил на конечном перемещении всех элементов механической системы:

.

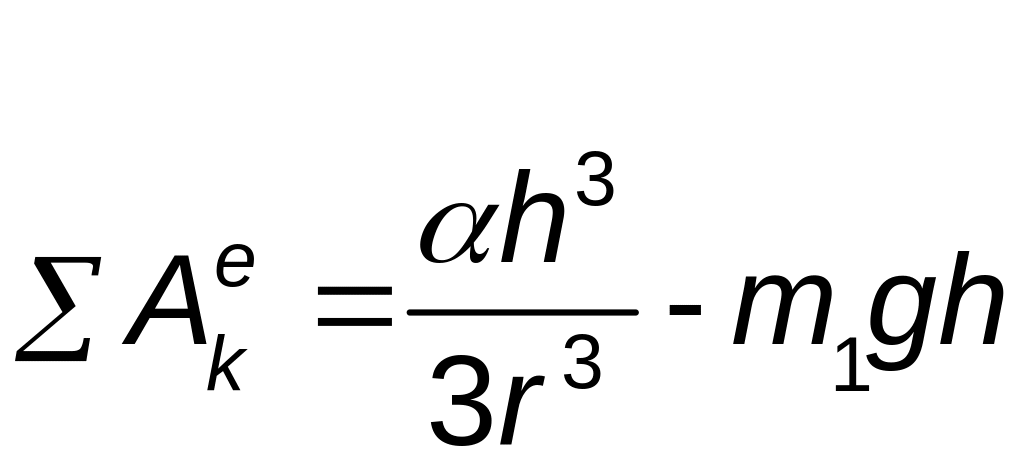Найдем уравнение, определяющее скорость груза А, для чего сравним изменение кинетической энергии системы на конечном перемещении с работой внешних сил, приложенных к системе, на данном перемещении: ,

тогда скорость груза равна: .

Пример решения контрольной работы КР Д.10:

Применение теоремы об изменении кинетической энергии к изучению движения механической системы. (приложение №5 к настоящему МП)

Дано: массы деталей: . Радиусы дисков: , Длина шатуна .

Путь пройденный грузом 1: . Радиусы инерции . Угол наклона плоскости движения груза 1: . Коэффициент трения груза 1: . Коэффициент сопротивления качению катка 5: . Сопротивление качению тела 2 не учитывать. Шатун 4 считать тонким однородным стержнем; каток 5 – однородный сплошной цилиндр. Массами звена ВС₅ и ползуна В пренебречь. На рисунке 155а показана механическая система в начальном положении.

Найти: - скорость груза 1 в конечном положении.

Решение:

Применим теорему об изменении кинетической энергии системы: , (1)

где и - кинетическая энергия системы в ее начальном и конечном положении. - сумма работ внешних сил, приложенных к системе, на перемещении системы из начального положения в конечное. - сумма работ внутренних сил системы на том же перемещении. Однако, для рассматриваемой системы, состоящей из абсолютно твердых тел, соединённых нерастяжимыми нитями и стержнями, .

Так как в начальном положении система находится в покое, то . Следовательно, уравнение (1) принимает вид: . (2)

Для определения кинетической энергии и суммы работ внешних сил надо рассмотреть систему в ее конечном положении (рис. 155б, в).

I. Напишем кинематические соотношения между скоростями и перемещениями точек системы, т.е. уравнения связей, при этом скорости и перемещения выразим соответственно через скорости и перемещения груза 1.

Скорость центра масс С катка 2 равна скорости груза 1: (3)

Угловая скорость катка 2, МЦС которого находитс в тч Р₂: , учитывая (3),

получим: . (4)

Скорость точки D катка 2: , т.е. .

Скорость точки Е блока 3 равна скорости точки D катка 2: , (5) но . Следовательно по (5) . Так как , то , откуда (6). Заменяя в формуле (6) и , получим

Или . После интегрирования этого выражения, при нулевых начальных условиях: (7) Когда груз 1 пройдёт путь , блок 3 повернётся на угол :

.

При этом повороте блока 3 на 180⁰ его точка А₀ перейдёт в конечное положение А и шатун 4 из начального положения А₀В₀ перейдёт в конечное положение АВ.

Каток 5 переместится влево при повороте блока 3 на угол и вправо при повороте блока ещё на ; значит, конечное положение катка 5 совпадает с его начальным положением.

Таким образом, конечное положение свей системы вполне определено (рис. 155 б).

II. Вычислим кинетическую энергию системы в конечном положении как сумму кинетических энергий тел 1, 2, 3, 4, 5: (8).

Кинетическая энергия груза 1, движущегося поступательно: . (9)

Кинетическая энергия катка 2, совершающего плоское движение, , (10)

где - момент инерции катка 2 относительно его продольной центральной оси :

(11)

Подставляя (3), (4), (11) в формулу (10), получим:

(12)

Кинетическая энергия тела 3, вращающегося вокруг оси ОХ, (13)

Где (14) Подставляя (6), (14) в формулу (13), получим:

(15)

Кинетическая энергия шатуна 4, совершающего плоское движение ,

Где - скорость центра масс шатуна 4; - угловая скорость шатуна 4; - момент инерции шатуна относительно центральной оси .

Для определения и найдём положение мгновенного центра скоростей шатуна 4. Так как скорости точек А и В в этот момент паралельны и равны по модулю, то МЦС шатуна находится в бесконечности, следовательно, его угловая скорость в данный момент , а скорости всех точеек шатуна парралельны и равны между собой. Таким образом, кинетическая энергия шатуна 4: , (16) где (17). Вращательная скоростьточки А тела 3: (18) или с учётом (6) . Поскольку , получим . По (17) , (19) После подстановки (19) в (16) выражение кинетической энергии шатуна 4 принимает вид: , (20)

Кинетическая энергия катка 5, совершающего плоское движение, , где - скорость центра масс катка 5; - момент инерции катка 5 (однородного сплошного цилиндра) относительно его центральной продолной оси , .

Так как каток катится без скольжения, то его МЦС находится в точке . Поэтому угловая скорость катка 5: . Следовательно: .

Так как звено совершает поступательное движение, то .

Поэтому выражение кинетической энергии катка 5 принимает вид:

(21)

Кинетическая энергия всей механической системы определяется по формуле (8) с учётом (9), (12), (15), (20), (21): .

Подставим сюда значения масс, получим: , или . (22)

III. Найдём сумму работ всех внешних сил, приложенных к системе, на заданном ее перемещении. Покажем внешние силы, приложенные к системе (рис. 155 в).

Работа силы тяжести : (23)

Работа силы трения скольжения :

Так как , то (24)

Работа силы тяжести : (25)

Работа сил сцепления , каткоа 2 и 5 равна нулю, т.к. эти силы приложены в МЦС этих катков.

Работа силы тяжести : , где - вертикальное перемещение центра тяжести шатуна 4 из начального положения в его конечное положение (рис. 155 г): , тогда:

(26)

Работа пары сил сопротивления качению катка 5: , (27)

Где - момент пары сил сопротивления качению катка 5; - угол поворота катка 5. Так как каток катится без скольжения, то угол поворота (28)

Где - перемещение центра тяжести катка 5.

В данном случае работу пары сил сопротивления вычислим как сумму работ этой пары при качении катка 5 влево при повороте тела 3 на угол и качении вправо, когда тело 3 повернётся ещё на угол .

Перемещение центра тяжести катка 5 равно перемещению ползуна В влево и вправо:

(29)

Определим перемещение при повороте тела 3 на угол . За начало отсчёта координаты точки В выберем неподвижную точку К плоскости (рис. 155 г). При этом повороте тела 3 шатун из положения перейдёт в положение . Тогда , где , , следовательно: , (30)

Подставляя (30) в (29), а затем в (28), находим полный угол поворота катка 5: (31). Работа пары сил сопротивления качению по (27):

. (32)

Сумма работ внещних сил определится сложением работ, вычисляемых по формулам (23)-(26) и (32):

Подставляя заданные значения масс, получим:

,

Или , (33)

IV. Согласно теореме (2), приравняем значения и , определяемые по формулам (22) и (33): , откуда: .

------------------------------------------------------------------------