Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

модуль Д.У..doc

Скачиваний:

Добавлен:

01.05.2025

Размер:

2.23 Mб

Скачать

☆

1 / 91 2 3 4 5 6 7 8 9 > Следующая >>>

Предисловие

Данное учебно-методическое пособие предназначено в первую очередь, для студентов экономико-управленческих специальностей; может быть полезным для всех категорий студентов, изучающих в том или ином объёме высшую математику. Пособие является дополнением к конспектам лекций по высшей математике часть I, а также руководством для подготовки и проведения практических занятий.

Пособие разбито на учебные элементы — занятия, каждое занятие содержит справочный материал (основные определения, формулы, признаки и т.п.), необходимый для решения задач. Каждый учебный элемент содержит три блока задач (аудиторные, домашние и дополнительные), при составлении которых особое внимание уделено стандартным задачам, которых так не хватает для успешного хода учебного процесса. Приводятся методические рекомендации по решению определённого круга задач, в частности, алгоритмы их решения. Такая форма изложения позволяет сначала познакомиться с приёмами решения типовых задач и оформлением записи их решения, а затем приступить к выработке навыков в их самостоятельном решении. Тем не менее, в пособии довольно много сложных заданий и устных вопросов. Приводится два варианта типовой контрольной работы, а также решение индивидуального домашнего задания. Среди устных заданий немало качественных вопросов, обычно предлагаемых на экзаменах по высшей математике, эта часть данного издания будет полезна студентам для подготовки к экзаменам.

Список обозначений:

▲ ▼ — важные определения;

[ — «обратите особое внимание!»

► ◄ — начало и конец решения.

Занятие 1

Дифференциальные уравнения с разделяющимися переменными и приводящиеся к ним

Цели

Знать:

Основные определения, связанные с понятием дифференциальные уравнения.

Уметь:

Определять, что функция удовлетворяет заданному дифференциальному уравнению;
находить решения дифференциального уравнения с разделяющимися переменными;
решать задачу Коши.

▼Дифференциальным уравнением называется уравнение относительно неизвестной функции и ее производных различных порядков, т.е.

.▲

▼Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.▲

▼Дифференциальное уравнение первого порядка в общем случае можно записать в виде

.▲ (1)

Если уравнение (1) можно разрешить относительно у', то его записывают в виде

. (2)

и называют дифференциальным уравнением первого порядка, разрешенным относительно производной.

Дифференциальное уравнение первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме:

P(x;y)×dx+Q(x;y)×dy=0, (3)

где Р(х;у) и Q(x;y) — известные функции.

▼Условие, что при х=x₀ функция у(x) должна быть равна заданному числу y_o, т.е. у=у₀, называется начальным условием (условие Коши). Начальное условие записывается в виде

или .▲ (4)

▼Дифференциальное уравнение вида

или

Р(х)dx + Q(y)dy=0, (5)

где Р(х) и Q(y) — непрерывные функции, называется уравнением с разделяющимися переменными (с разделенными переменными).▲

▼Уравнения с разделяющимися переменными в общем случае имеет вид

.▲ (6)

Общий интеграл этого уравнения имеет вид

Уравнение , где а, b, с — числа, путем замены ах+by+с=u сводится к дифференциальному уравнению с разделяющимися переменными. Дифференцируя по х, получаем:

Данное уравнение принимает вид , откуда следует .

Интегрируя это уравнение и заменяя u на ах+by+с, получим общий интеграл исходного уравнения.

Постановка задачи 1: Доказать, что функция у=у(х) удовлетворяет дифференциальному уравнению .

План решения: 1. Вычислить производную ;

2. Подставить у(х) и в уравнение ;

3. Убедиться в том, что получается тождество, т.е. для всех допустимых х.

№ 1. Проверить, что функция у=х+С есть общее решение дифференциального уравнения , и найти частное решение, удовлетворяющее начальному условию . Дать геометрическое истолкование.

►Функция у=х+С удовлетворяет данному уравнению при любых значениях произвольной постоянной С. В самом деле, . Зададим произвольное начальное условие . Полагая х=х₀ и у=у₀ в равенстве у=х+С, найдём, что С=у₀-х₀. Подставив это значение С в данную функцию, будем иметь у=х+у₀-х₀. Эта функция удовлетворяет заданному начальному условию. В самом деле, положив х=х₀получим у=х₀+у₀-х₀=у₀. Таким образом функция у=х+С является общим решением данного дифференциального уравнения. В частности, полагая х₀=0 и у₀=0, получим частное решение у=х.

Общее решение данного дифференциального уравнения, т.е. функция у=х+С определяет в плоскости семейство параллельных прямых с угловым коэффициентом k=1 (см. рис. 1).

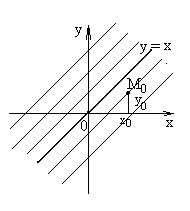
Рис.1

Через каждую точку М₀(х₀;у₀) плоскости проходит единственная интегральная линия у=х+у₀-х_0.Частное решение у=х определяет одну из интегральных кривых, а именно прямую проходящую через начало координат.◄

№2. Проверить, является ли функция общим решением или общим интегралом уравнения .

►Необходимо проверить два условия:

1) удовлетворяет ли функция дифференциальному уравнению при любом С;

2) для всякого ли начального условия у=у₀при х=х₀ найдётся С=С₀.

В результате дифференцирования функции заданной неявно получим . Отсюда .

Подставив это значение в исходное уравнение, получим тождество.

Итак, первое условие выполняется, указанная функция является решением уравнения.

Проверим второе условие. Зададим начальные условия . Запишем данную функцию в виде . Так как , то и , но это верно лишь при условии .

Если взять точку (х₀; у₀) вне окружности с центром в начале координат и радиусом R=2, то получим , что невозможно ни при каких действительных значениях С. Следовательно, выражение не является общим интегралом данного уравнения.◄

Постановка задачи 2: Решить уравнение вида .

План решения: 1. Убедиться, что уравнение с разделяющимися переменными, для этого исходное уравнение привести к виду

или или — уравнения с разделяющимися переменными в общем виде; или в дифференциальной форме: ;

2. Обе части уравнения умножаем на dx (вообще говоря, нужно сделать так (используя различные алгебраические приемы), чтобы дифференциалы и стояли в числителях, а не в знаменателях);

;

3. В области, где и разделяем переменные, т.е. представляем уравнение в виде

;

(другими словами делаем так, чтобы каждая из функций «стояла у своего дифференциала», то есть где - там , где - );

Замечание. Если одно или оба уравнения и имеют решения х₁, х₂, …, и у₁, у₂, …, то равенства х=х₁, х=х₂, … и у=у₁, у=у₂, … нужно присоединить к ответу, так как они являются особыми решениями исходного уравнения.

4. Вычислим интегралы в уравнении

Константа С при этом есть произвольная постоянная интегрирования, которую достаточно прибавить к первообразной в любой части равенства;

5. Полученное выражение преобразуем к виду при всевозможных значениях С.

№3. Решить уравнение .

►1)Данное уравнение — уравнение с разделяющимися переменными, так как оно имеет вид . В данном случае , , , .

2) Обе части уравнения умножать на dx не надо, так как уравнение уже имеет нужный вид, а именно:

, теперь разделим «на стоящую не у своего дифференциала функцию» :

. То есть получили вид , где и .

3)В области, где разделяем переменные, т.е. представляем уравнение в виде

В нашем случае надо разделить обе части уравнения на y:

, . В результате этих действий переменные разделились. Слева при присутствует только y (нет «иксов»), а справа при присутствуют только «иксы» (нет «игреков»).

4)Интегрируем обе части уравнения:

. Получаем: . Отметим, что постоянную интегрирования в выражение для общего решения можно вводить в произвольном виде так, как это удобно в конкретной ситуации, например, -С, , , , . Поэтому можем написать . Упрощаем: