Решение

Луч от источника S падает на пластинку, частично преломляясь и отражаясь в точках A, B, C, и D (см. рис. 2.1).

Отражение луча в точках В и С не сопровождается потерей полуволны, т.к. в этих точках идет отражение от оптически менее плотной среды.

Следовательно, оптическая разность хода лучей SABK и SABCD

∆= 2(BC)n₂ ─ (ВК)n₁;

где n₁ – показатель преломления воздуха; n₂ – показатель преломления пленки;

BC = AB

- угол падения;

- угол преломления;

d – толщина пленки;

KBE = α, т.к. луч выходит из пластинки параллельно падающему лучу.

KDB = KBE = α, как два угла с взаимно перпендикулярными сторонами (KD _┴ BK; BM _┴ BE)

Очевидно, что АВ = BK = (DB)sinα;

(DB) = 2(BM)

(BM) найдем из ∆ BCM:

BCM = , BM = d*tg

Следовательно, BK = (DB)sin = 2(BM)sin = 2d*tg sin

В соответствии с этим

∆ = =

Учитывая, что

; sinα = ;

получаем:

∆ = = =

∆ = = 2d*

Условием максимума, т.е. условием того, что пленка будет казаться окрашенной, является

∆ = kλ

подставляя в это условие раннее выведенное выражение для оптической разности хода ∆, получим:

= kλ

Для минимальной толщины пленки k =1, так что

d_min = ;

d_min = 2,89*10^-5 см.

Ответ: d_min = 2,89*10^-5 см.

Задача №2.2

К

S

K

ольца Ньютона наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной толстой стеклянной пластинки и плоско-выпуклой линзы с радиусом кривизны R = 0,96 м.. Роль тонкой пленки, от которой отражаются когерентные волны, играет воздушный зазор между пластинкой и линзой. Между светлыми кольцами Ньютона с номерами m = 7 и n = 5 расстояние l = 0,31 мм. Найти длину волны монохроматического света,

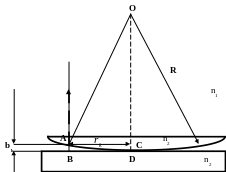п адающего нормально на установку. Наблюдения проводятся в отраженном свете.

Дано:

l = 0,31 мм

n

m

R

Найти:

λ = ?

Решение

Интерференция будет наблюдаться вблизи точки D (в месте соприкосновения пластинки и линзы), т.е. там, где воздушный клин, который образуется между пластинкой и линзой имеет очень малую толщину и поэтому лучи отраженные от нижней поверхности линзы и верхней поверхности пластинки будут когерентными.

Поэтому можно считать, что свет падает по нормали к пластинки;

Для наглядности рассматриваем лучи не в (.) D, а дальше от центра – в (.)В.

Когда падающий луч доходит до точки А, лежащей на нижней поверхности линзы, то луч SA в точке А:

частично отражается, - это луч АК,

частично преломляется: - это луч AB.

На верхней поверхности пластинки в точке В луч опять частично отражается и частично преломляется, но т.к. наблюдение ведется в отраженном свете, то рассматриваем только отразившийся луч ВК.

В точке А будет наблюдаться интерференция, т.е. наложение двух когерентных лучей АК и ВК (луча отразившегося от нижней поверхности линзы АК и луча отразившегося от верхней поверхности пластинки луча ВК).

Найдем радиусы светлых колец Ньютона:

Чтобы вывести формулу для радиуса светлого кольца надо записать условие для максимума интенсивности:

(Для I_max):

Оптическая разность хода ∆ луча АК и луча ВК равна:

∆ = 2АВn_{1 + ;}

Здесь необходимо было учесть условие того, что при отражении от оптически более плотной среды происходит скачок фазы светового вектора на π, для чего необходимо прибавлять (в точке В имеется отражение от оптически более плотной среды).

В рассматриваемом случае имеются две точки в которых лучи отражаются: - это точка А, где отражается луч АК и точка В, где отражается луч ВК.

В точке А фаза светового вектора луча АК не претерпевает скачка, т.к.

луч АК проходит в линзе – в среде оптической более плотной, чем воздух, а отражается от воздуха, среды оптически менее плотной (линза имеет показатель преломления n₂ > n₁ )

В точке В происходит скачок фазы, т.к. луч ВК идет в воздухе , а отражается от линзы, среды оптически более плотной.

Определим радиус светлого кольца:

В ∆ ОАС:

катет АС – равен радиусу светлого кольца r_m

катет ОС = ОD – СD = R – AB;

АО – равен радиусу линзы R

Величина воздушного зазора АВ равна отрезку СD

По теореме Пифагора:

(АО)² = R² = (ОС)² + (АС)² = (ОD-СD)² + (AC)² = (R-AB)² + r_m = (R - b_m)² + r_m²

R² = (R - b_m)² + r_m²

R² = R² -2Rb_m + b_m² + r_m²

2Rb_m = r_m²

(слагаемым b_m² пренебречь, как величиной второго порядка малости.)

Отсюда:

b_m =

Дифракция

Задача№1

На диафрагму с круглым отверстием падает нормально параллельный пучок монохроматического света λ=0,6 мк м. На экране наблюдается дифракционная картина. При каком наибольшем расстоянии между диафрагмой и экраном в центре дифракционной картины будет наблюдаться темное пятно? Диаметр отверстия равен 1,96 мм.

Ответ: r =0,71м.

Задача №2

Радиус r₄ четвертой зоны Френеля для плоского волнового фронта равен 3 мм. Определить радиус r₆ шестой зоны Френеля.

Ответ: r₆ = 3,69 мм.

Задача №3

Расстояние между точечным источником света с длиной волны λ = 0,63мкм и экраном равно 3,5м.Диафрагма с отверстием радиуса r находится в k раз (k=3,7) ближе к экрану, чем к источнику. В отверстии укладывается m =2 зон Френеля. Определить радиус отверстия r.

Ответ: r =0,86мм.

Задача №4

Свет от монохроматического источника (λ = 600 нм) падает нормально на диафрагму с диаметром отверстия d = 6мм . За диафрагмой на расстоянии l = 3м от нее находится экран. Какое число k зон Френеля укладывается в отверстии диафрагмы? Каким будет центр дифракционной картины на экране: темным или светлым ?

Ответ: k = 5; центр дифракционной картины будет светлым.

Задача № 5

Найти радиусы r_k первых пяти зон Френеля, если расстояние от источника света до волновой поверхности a = 1м , расстояние от волновой поверхности до точки наблюдения b = 1м. Длина волны света λ = 500 нм.

Ответ:;

r₁ = 0,50 мм; r₂ = 0,71 мм; r₃ = 0,86 мм; r₄ = 1,0 мм; r₅ = 1,12 мм.

Задача № 6

Дифракционная картина наблюдается на расстоянии l от точечного источника монохроматического света с длиной волны λ = 600 нм. На расстоянии а = 0,5l от источника, помещена круглая непрозрачная преграда диаметром D = 1 см. Найти расстояние l, если преграда закрывает только центральную зону Френеля.

Ответ: l = 167 м.

Задача № 7

Точечный источник света с длиной волны λ = 0,50 мкм расположен на расстоянии а = 100 см перед диафрагмой с круглым отверстием радиуса r равным 1,0 мм. Найти расстояние b от диафрагмы до точки наблюдения, для которой число зон Френеля в отверстии составляет k = 3.

Задача №8

Спектры дифракционной решетки проектируются на экран, расположенный параллельно решетке на расстоянии 1,8 м от нее. Определить длину волны монохроматического света, падающего на решетку, если расстояние от второго спектра до центральной светлой полосы 21,4 см. Решетка содержит 100 штрихов на 1 мм.

Задача №9

На дифракционную решетку в направлении нормали к ее поверхности падает монохроматический свет. Период решетки равен 2 мкм. Дифракционный максимум какого наибольшего порядка дает эта решетка в случае красного

(λ_кр. = 0,7 мкм) и фиолетового (λ_ф. = 0,45 мкм) света?

Задача №10

Дифракционная решетка содержит 100 штрихов на 1 мм длины решетки. Определить длину волны монохроматического света, падающего на решетку нормально, если угол между двумя спектрами первого порядка равен 8⁰.

Ответ: λ = 1,7 мкм.

Задача №11

Дифракционная решетка содержит 200 штрихов на 1мм длины решетки. На дифракционную решетку падает нормально монохроматический свет длиной волны λ = 600 нм. Найти общее число дифракционных максимумов которые дает эта решетка.

Задача №12

Дифракционная решетка содержит n = 200 штрихов на 1 мм. На решетку падает нормально монохроматический (λ = 0.6 мкм). Максимум какого наибольшего порядка дает решетка? Найти общее число дифракционных максимумов, которые дает эта решетка.

Задача №13

На щель шириной 2 мкм падает нормально параллельный пучок монохроматического света с длинной волны λ =0,5 мкм . Найти ширину изображения щели на экране, удаленном от щели на е = 1 м. Шириной изображения считать расстояние между первыми дифракционными минимумами, расположенными по обе стороны от главного максимума освещенности.

Задача №14

Расстояние между экраном и дифракционной решеткой, имеющей 125 штрихов на 1 мм, равно 2,5 м. При освещении решетки светом с длиной волны 420 нм на экране видны сини линии. Определить расстояние от центральной линии до первой линии на экране

Пример решения задач

Задача №3.1.1

На диафрагму с круглым отверстием радиусом r = 1 мм падает нормально параллельный пучок света с длиной волны λ = 0,5 мкм. На пути лучей, прошедших через отверстие, помещают экран. Определить максимальное расстояние b_max от центра отверстия до экрана, при котором в центре дифракционной картины еще будет наблюдаться темное пятно.

Дано:

r = 1 мм

λ = 0,5 мкм

в центре картины еще

наблюдается темное пятно

Найти:

b_max─?