
- •Раздел 3.3 Характеристики системы индуктор загрузка.
- •Раздел 3.4 Электромагнитное поле в проводящей среде.
- •Раздел 3.4.2 Влияние электрофизических свойств проводящего тела
- •Раздел 3.4.3 (влияние геометрических параметров)
- •Раздел 3.5 э.М. Волны в непроводящей среде
- •Раздел 3.6 Методы расчета системы индуктор загрузка.
- •Раздел 3.7.1 Электродинамические силы при индукционном нагреве
- •Раздел 4.1 Принцип действия и основные характеристики
- •Раздел 4.2 Физические основы нагрева диэлектриков
- •Раздел 4.3 Математическое описание диэлектрического нагрева
- •Раздел 4.4 Инженерный расчет рабочего конденсатора
- •Раздел 5.1 Виды электрических разрядов в газах
- •Раздел 5.2 Физика дугового разряда
- •Раздел 5.2.1 Процессы в столбе дуги
- •Раздел 5.2.2 Процессы в приэлектродных областях
- •Раздел 5.3 Электрическая дуга постоянного тока(свободно горящая)
Раздел 3.5 э.М. Волны в непроводящей среде
Для исследования электромагнитного поля в зазоре и на других участках системы и-з т.е на участках 3,4,5 можно использовать исходное дифференциальное выражение:
![]()
Здесь коэффициент
![]()
Уравнение можно использовать только в том случае, когда электромагнитные волны имеют простую конфигурацию, т.е. волны плоские ил цилиндрические
Для цилиндрических электромагнитных волн уравнение имеет вид:
![]()
Если ввести
переменную
![]() ,
то уравнение представляется обычным
дифференциальным уравнением Бесселя
нулевого порядка
,
то уравнение представляется обычным
дифференциальным уравнением Бесселя
нулевого порядка
Рассмотрим э.м. поле в пустом цилиндрическом индукторе, т.е. в индукторе без загрузки
С учетом значений частот и радиусов индуктора, обычно применяемых в индукционных установках , выполняется условие:
![]()
для таких малых значений аргумента возможна замена функций Бесселя их приближенными значениями и можно принять следующие формулы для H,E и S
![]()
![]()
![]()
Аналогично
рассчитываются значения напряженностей
, cсозданных
токами все витков индуктора. Затем все
рассчитанные составляющие напряженностей
магнитного поля по
![]() суммируются и находится результирующее
значение
суммируются и находится результирующее
значение
![]()
Для единичного объема пространства удельная реактивная мощность, pv рассчитывается по формуле.
![]()
Реактивная мощность
в кольце с номером
![]() объемом
объемом
![]()
![]()
Отсюда реактивная
мощность
![]()
Раздел 3.6 Методы расчета системы индуктор загрузка.
Метод индуктивно связанных контуров
Этот метод является одной из разновидностью методов расчета, основанных на использовании схем замещения.(второе название метод интегральных уравнений)
Используемые допущения:
1) Считаем, что ток течет в загрузке и в индукторе течет только в слое, равном глубине проникновения
2) все материалы неферромагнитные
3) плотности токов в слое сonst
![]()
![]() вносят наибольшую
погрешность
вносят наибольшую
погрешность
Для того чтобы представить наши катушки соленоидами, необходимо чтобы
![]()
![]()
Далее как в тоэ нарисуем схему замещения линейного трансформатора
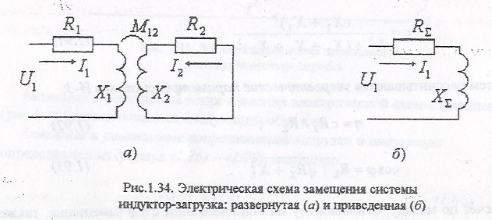 Т
Т
аким образом мы переходим от полевой задачи к задачи теории цепей
1-ое уравнение
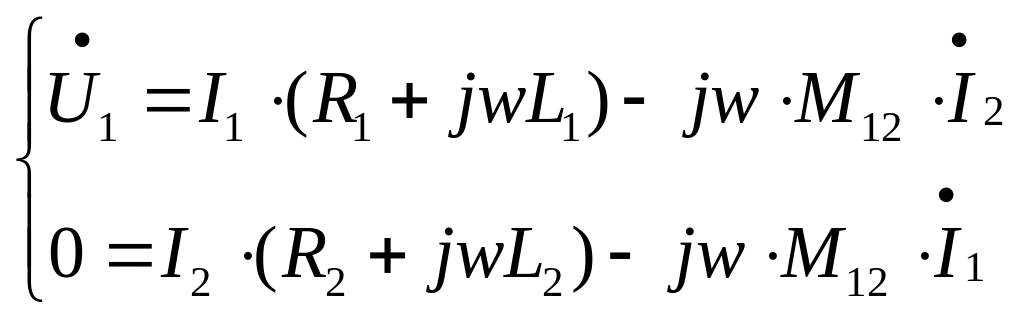
Определяется свойствами индуктора и загрузки, их геометрией и взаиморасположением.
U1 как правило исходные данные
I1, I2- как правило надо найти
Самое главное найти I1, I2 нам особо не нужен
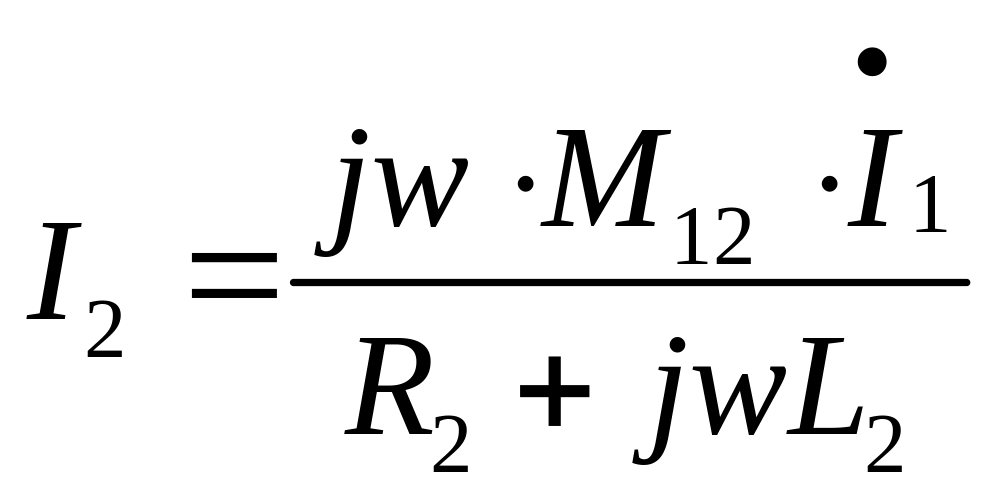
Водится специальный коэффициент связи
![]()
Показывает эффективность э.м. связи между индуктором и загрузкой
Индуктор создал поток Ф1
Фсц- сцепленный магнитный поток и с индуктором и с загрузкой
![]()
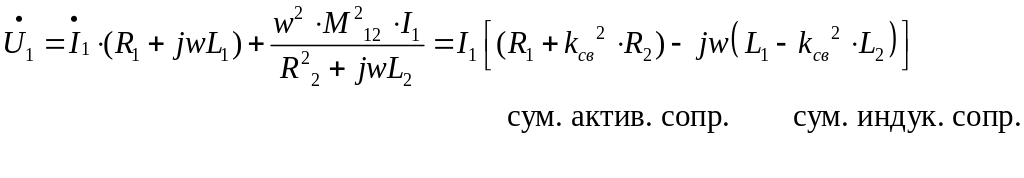
если индуктор пустой, то коэффициент связи будет равен 0
Мы рассмотрели простейший вариант метода индуктивно связанных контуров- его основной недостаток
допущение 3 -плотности токов const
Чтобы этого не было используют метод индуктивных связанных контуров в одномерной или двумерной постановке
Индуктор и загрузку разбиваем на кольца
уравнений будет столько, сколько колец
Допущение 3 снимается, но не учитываем краевые эффекты, чтобы учесть краевые эффекты, разбиваем по оси z
Получаем систему линейных алгебраических уравнений
Ответом будут токи во всех кольцах
![]()
![]()
Мощность в индукторе
![]()
Мощность в загрузке
![]()
![]()
Электрический кпд
![]()
Полная мощность
![]()
![]()
Это самый точный метод, но подходит только для линейных систем
