Раздел 3.3 Характеристики системы индуктор загрузка.
При рассмотрении хар-к системы индуктор- загрузка воспользуемся идеей о декомпозиции расчетной области.(Вайнберг, 60-гг)
Расчетная область пространства с э/м системой индуктор-загрузка(индуктор цилиндрический охватывающий)
Принцип декомпозиции расчётной области заключается в том, что мы нашу расчётную область разбиваем на подобласти.
Суммарная активная
мощность системы равняется
Далее рассчитываем
суммарную реактивную мощность
Находим полную
мощность и-з
Далее все определяется тем, чем мы задаемся:
В практических
задачах чаще задается напряжение, тогда
Электрический КПД
системы индуктор загрузка:
системы и.з.
Водится понятие идеальная система индуктор – загрузка(в системе отсутствует воздушный зазор):
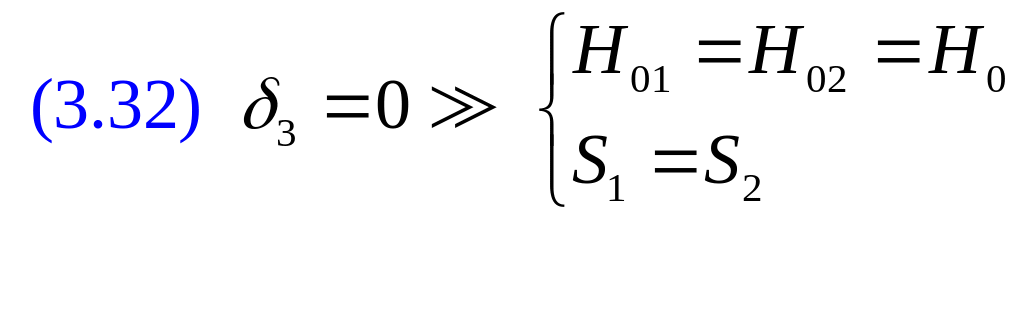
Вспомним формулу
Она справедлива как для индуктора, так и для загрузки. С ее помощью получим выражение для электрического кпд идеальной системы и-з.
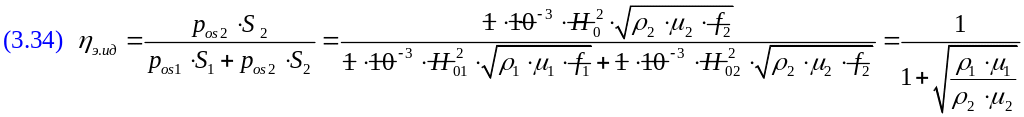
Таким образом, чтобы иметь побольше кпд, нужно
1)
поменьше (алюминий, медь высокого
качества- мат. с высокой проводимостью)
2)
побольше
(ферромагнитные материалы-стали-)
Охлаждение
используют при больших тепловых потерях
и больших
Крио-резистивный
эффект - снижение
почти до нуля
относительный
размер загрузки
Как выбрать частоту
Пусть
,
тогда
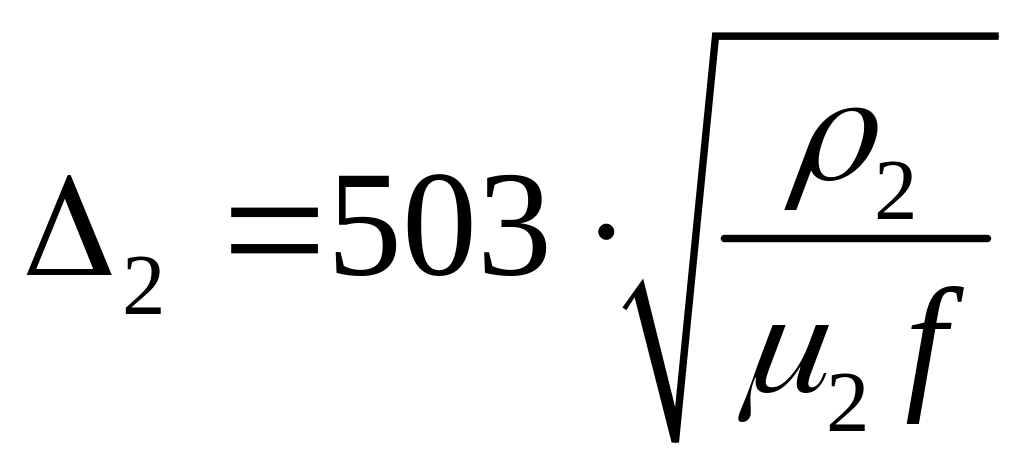Подставляем
,
получаем
Отсюда
Далее берем стандартную частоту из
ряда частот, на которые делаются источники
питания 50 Гц, 500 Гц, 1000 Гц, 2.4 кГц, 8 кГц, 10 кГц, 64 кГц и т.д.
Некоторые делаются на нестандартные частоты
Очень большая проблема- выбор частоты , есть разные режимы и этапы плавки.
Есть холодный режим, переходной, горячий режим (плавка в индукцион. тигельной печи кусковой феромагн. стали)
Единственная возможность уменьшить реактивную мощность – это уменьшить Q4
Для ее уменьшения используют феромагнитные экраны
сумм. сечение
пакетов определяется магнитным потоком
обратного замыкания
Число пакетов выбирается из условий наиболее эффективного естественного воздушного охлаждения пакетов, чтобы избежать перегрева магнитопровода
Здесь появляются
потери
,
потери
в магнитопроводе
На больших частотах используют электромагнитные экраны, выполненные из материалов с высокой электрической проводимостью
за пределами экрана
если частота 50
Гц,
В уравнение появится
третье слагаемое(потери в экране)
Применение феромагнитных и э.м экранов приводит к уменьшению размеров пр-ва и снижению Q4, а значит к увелич.
Другие конфигурации системы индуктор-загрузка
-плоский
-система с внутренним индуктором
-нагрев в поперечном магнитном поле
-индукционная стержневая система
-индукционная резистивная система
Раздел 3.4 Электромагнитное поле в проводящей среде.
подраздел 3.4.1 электромагнитная волна в полубесконечном теле
это
основное уравнение, описывающее изменение
напряженности магнитного поля в
проводящей среде
Где
коэффициент,
характеризующий свойства среды
Выведем это уравнение:
закон
Максвелла
,
тогда
,
переходим из временной области
,
-это
некоторое комплексное число
, так как у нас
волна меняется по оси z
,то
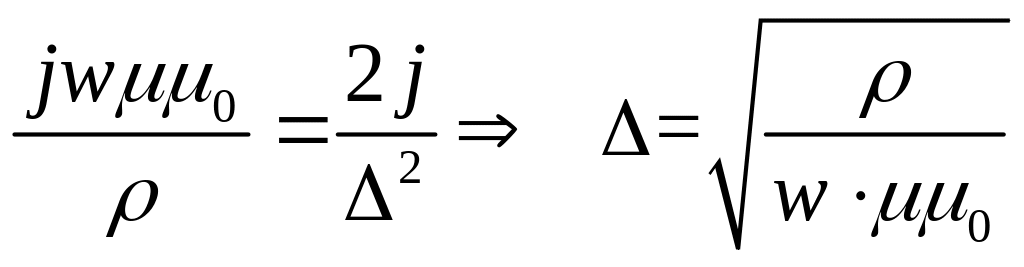получили формулу
для глубины проникновения
Решаем дифференциальное уравнение
Г.У.
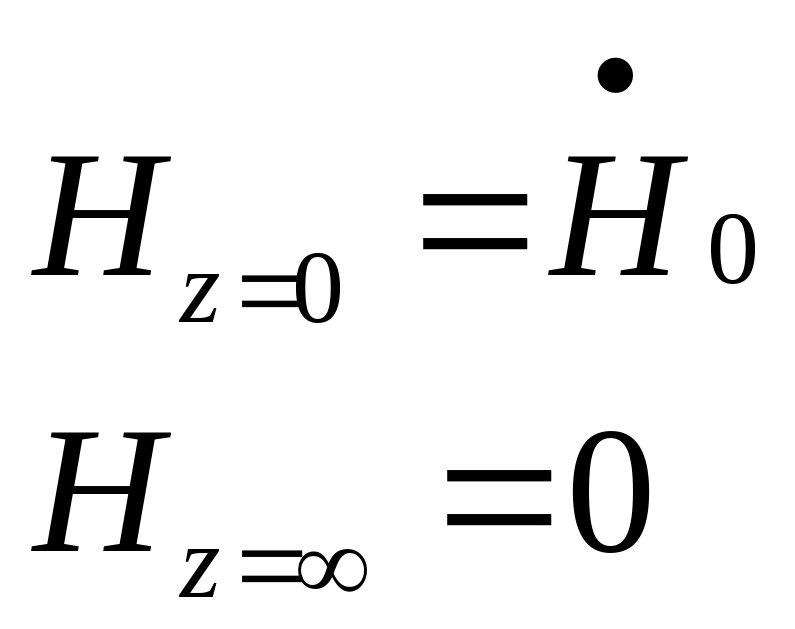
Решение
дифференциального уравнения имеет
вид
С1, C2- характеризуют параметры прямой и обратной волны при проникновении э.м волны в среду
После подстановки граничных условий получим формулу для напряженности магнитного поля в полубесконечном теле
Связь между
После подстановки H и дифференцирования получаем:
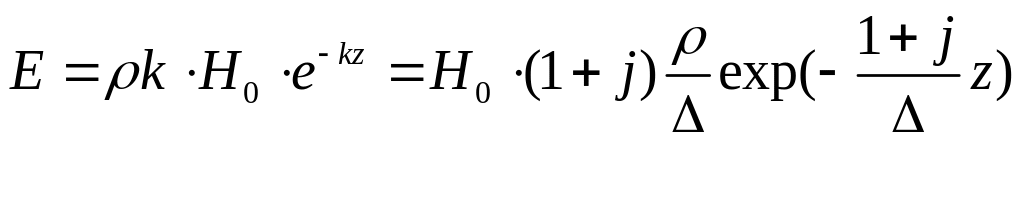или введя
соответствующее обозначение:
Вектор потока
Энергии(вектор Умова-Пойтинга) определяется
по формуле
,
где
-
комплексно –сопряженная с H
величина
С учетом полученных
выше выражений получим
Выражение для потока энергии может быть представлено также в виде:
Здесь
