Основные тождества алгебры множеств
Для любых множеств A, B, C справедливы следующие тождества:
1. Коммутативность. а) A B = B A ; б) A B = B A. |
2. Ассоциативность. а) A (B C) = (A C) C; б) A (B C) = (A B) C. |
3. Дистрибутивность. а) A(BC) = (AB)(AC); б) A(BC) = (AB)(AC). |
4. Закон де Моргана. а)
б)
|
5. Идемпотентность. а) A A = A; б) A A = A. |
6. Поглощение. а) A (A B) = A; б) A (A B) = A. |
7. Расщепление (склеивание). а) (A B) (A ) = A; б) (A B) (A ) = A. |
8. Двойное дополнение.
|
9. Закон исключенного третьего. A
=
U. |
10. А\В = A .
|
11. Операции с пустым и универсальным множествами. а)
A
U
= U; в)
A
U
= A;
д)
б)
A
= A; г)
A
= ; е)
|
|
=
;
=
.
= A.
=
U;
=
.
Чтобы доказать некоторое тождество A = B, нужно доказать, что, во-первых, если x А, то xВ и, во-вторых, если xВ, то x А.
Пример 1.8. Докажем таким образом, например, свойство дистрибутивности для объединения (тождество 3а):
A (BC) = (AB) (AC).
1. Сначала предположим, что некоторый элемент x принадлежит левой части тождества, т.е. x A (BC), и докажем, что x принадлежит правой части, т.е. x(AB) (AC).
Действительно, пусть x A (BC). Тогда либо x A, либо x BC. Рассмотрим каждую из этих возможностей.
Пусть x A. Тогда x A B и x A C (это верно для любых множеств B и C). Следовательно, x(AB) (AC).
2. Предположим, что некоторый элемент x принадлежит правой части тождества, т.е. x (AB) (AC), и докажем, что x принадлежит левой части, т.е. x A (BC) .
Действительно, пусть x (AB) (AC). Тогда xAB и одновременно x AC. Если x AB, то либо x A, либо x B, если .x AC, то либо x A, либо x C. Пусть x A, тогда x A (BC) и утверждение доказано. Если x A, то одновременно должны выполняться условия x B и x C, т.е. x BC. Но тогда x BC и x A (BC), что также доказывает наше утверждение.
Доказательство тождеств можно проиллюстрировать с помощью диаграмм Венна. Основные тождества алгебры множеств можно использовать для доказательства других тождеств.
Пример 1.9. Доказать тождество (AB) \ В = A .
Преобразуем левую часть тождества, используя тождество 10:
(AB) \ В = (AB) .
Затем используем закон дистрибутивности (тождество 3б):
(AB) = A B .
Используем закон исключенного третьего (тождество 9): B = .
Получим A B = A . Используем свойство пустого множества (тождество 11б): A = A . Тождество доказано.
Пример 1.10. Доказать тождество: A \ (В \ C) = (A \ В) (A C).
Множества, стоящие в левой и правой частях тождества, изобразим с помощью диаграмм Эйлера – Венна (рис. 1.2).
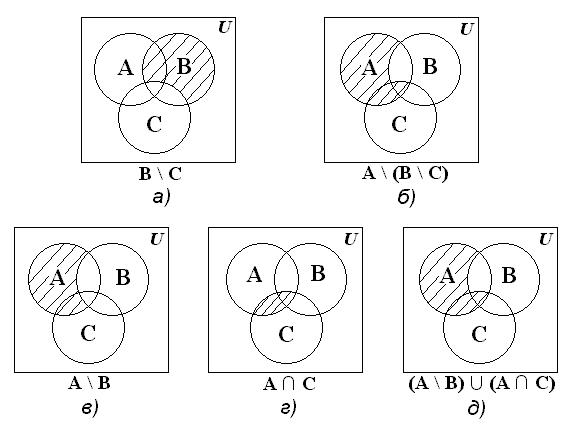
Рис. 1.2
Рисунки 1.2б и 1.2д иллюстрируют равенство множеств A\(В\C) и (A\В)(AC). Докажем тождество из нашего примера, воспользовавшись тождествами:
А\В
=A
,
=
,
= A,
A(BC)
= (AB)(AC).
Получим:
A\(В\C)
= A
=A
= A(
)
= A(
C)
=
=
(A
)(AC)
= (A\В)(AC).
Основные тождества алгебры множеств можно также использовать для упрощения формул.
Пример 1.11. Упростить выражение: (AB) ( B) (A ).
Используя закон коммутативности (тождество 1б), поменяем местами вторую и третью скобки:
(AB) ( B) (A ) = (AB) (A ) ( B).
Применим закон расщепления (тождество 7а) для первой и второй скобок:
(AB) (A ) ( B) = A ( B).
Воспользуемся законом дистрибутивности (тождество 3б):
A ( B) = A A B.
Используем закон исключенного третьего (тождество 9): A = .
Получим A A B = A B. Используем свойство пустого множества (тождество 11б): A B = A B. Итак, (AB) ( B) (A ) = A B.