23

КРАТНЫЕ ИНТЕГРАЛЫ

1. Двойной интеграл

1.1. Основные понятия и определения

Пусть в замкнутой области D плоскости Оху задана непрерывная

функция z = f ( x, y ). Разобьем область D на n “элементарных

областей” D_i , i = 1,2,..., n, площади которых обозначим через S_i ,

а диаметры (наибольшее расстояние между точками области) –

через d _i ( рис. 1). Рис.1.

В каждой области D_i выберем произвольную точку M _i ( x _i , y _i ),

умножим значение f (x _i , y _i) функции в этой точке на S_i и составим сумму всех таких произведений:

f (x₁, y₁)ΔS₁ + f (x₂, y₂)ΔS₂ + … + f (x_n, y_n)ΔS_n = ΔS_i . (1)

Эта сумма называется интегральной суммой функции f ( x, y) в области D.

Пусть d = d_i. Если при d → 0 существует предел интегральных сумм (1), не зависящий ни от способа разбиения области D на элементарные области, ни от выбора точек

M _i ( x _i , y _i ) в элементарных областях, то он называется двойным интегралом от функции

f ( x, y ) по области D и обозначается символом . Т.о., по определению,

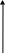
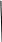
= . (2)

Из приведенного выше определения двойного интеграла следует, что

т.к. предел интегральных сумм не зависит от способа разбиения области

D на элементарные области, то ее можно разбивать и на участки прямыми,

параллельными координатным осям (рис.2). При этом S_i = х_i у_i .

Поэтому равенство (2) можно записать в виде Рис.2.

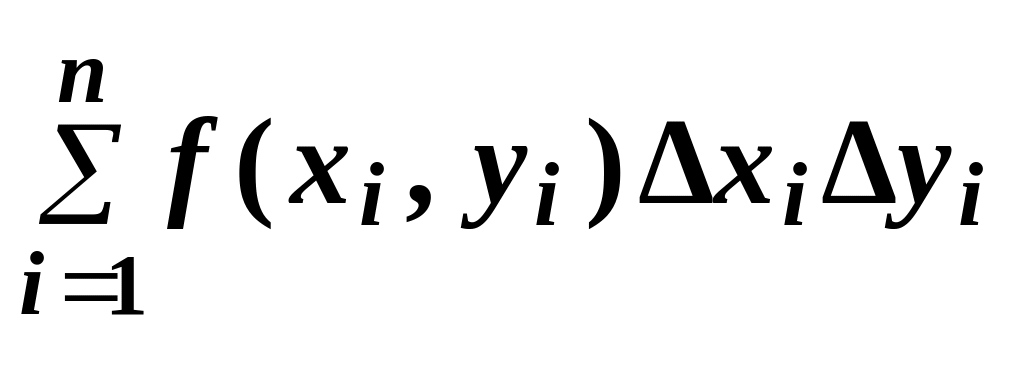= . (3)

Функция f ( x, y ) при этом называется интегрируемой в области D ( f ( x, у) – подынтегральная функция; f ( x, y) dx dy или f ( x, y) dS – подынтегральное выражение;

dS или dx dy – дифференциал (или элемент) площади; область D – область интегрирования; точка М ( х, у) – переменная точка интегрирования ).

Достаточные условия интегрируемости

Теорема 1. Всякая функция f ( x, y), непрерывная в ограниченной замкнутой области D, интегрируема в этой области.

Теорема 2. Если функция f ( x, y) ограничена в замкнутой ограниченной области D и непрерывна всюду в D, кроме некоторого множества точек площади нуль, то эта функция интегрируема в области D.

Замечание. Далее будем рассматривать только функции, непрерывные в области интегрирования, которые, согласно теореме 1, и интегрируемы в данной области.

1.2. Геометрический и физический смысл двойного интеграла

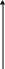
Объем цилиндрического тела

Рассмотрим тело, ограниченное сверху поверхностью z = f ( x, y )  0,

снизу – замкнутой областью D плоскости Оху, с боков – цилиндри-

ческой поверхностью, образующая которой параллельна оси Оz, а

направляющей служит граница области D (рис. 3). Такое тело назы-

вается цилиндрическим. Найдем его объем V.

Для этого разобьем область D (проекция поверхности z = f ( x, y ) на

плоскость Оху) произвольным образом на n областей D_i , площади которых Рис.3.

равны S_i , i = 1,2,..., n. Рассмотрим цилиндрические столбики с основаниями D_i , ограниченные сверху кусками поверхности z = f ( x, y ). В своей совокупности они составляют все рассматриваемое цилиндрическое тело.

Обозначим объем столбика с основанием D_i через V_i , получим V = . Возьмем на

каждой площадке D_i произвольную точку M _i ( x _i , y _i ) и заменим каждый столбик прямым цилиндром с тем же основанием D_i и высотой z_i = f ( x _i , y _i ). Объем этого цилиндра приближенно равен объему V_i цилиндрического столбика, т.е. V_i ≈ f ( x _i , y _i ) · S_i . Тогда получаем:

V = ≈ f ( x _i , y _i ) · S_i . (4)

Это равенство тем точнее, чем больше число n и чем меньше размеры «элементарных областей» D_i . Естественно принять предел суммы (4) при условии, что число площадок D_i неограниченно увеличивается (n → ∞), а каждая площадка стягивается в точку (d = d_i → 0), за объем цилиндрического тела, т.е. V = f ( x _i , y _i ) S_i , или, согласно равенству (3),

V = . (5)

Т.о., величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.

Масса плоской пластинки

Требуется найти массу m плоской пластинки D, зная что ее поверхностная плотность

γ = γ ( x, y ) есть непрерывная функция координат точки ( x, y ). Разобьем пластинку D произвольным образом на n элементарных частей D_i , площади которых равны S_i , i = 1, 2, … , n.

В каждой области D_i возьмем произвольную точку M _i ( x _i , y _i ) и вычислим плотность в ней

γ ( x _i , y _i ).

Если области D_i достаточно малы, то плотность в каждой точке ( x, y ) D_i мало отличается от значения γ ( x _i , y _i ). Считая приближенно плотность в каждой точке области D_i постоянной, равной γ ( x _i , y _i ), можно найти ее массу m _i : m _i ≈ γ ( x _i , y _i ) · S_i .

Т.к. масса m всей пластинки D равна m = , то m _i ≈ γ ( x _i , y _i ) · S_i . (6)

Точное значение массы получается как предел суммы (6) при условии n → ∞ или d = d_i → 0:

m = γ ( x _i , y _i ) S_i , или, согласно равенству (3),

m = . (7)

Т.о., двойной интеграл от функции γ ( x, y ) численно равен массе пластинки, если подынтегральную функцию γ ( x, y ) считать плотностью этой пластинки в точке ( x, y ). В этом состоит физический смысл двойного интеграла.