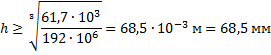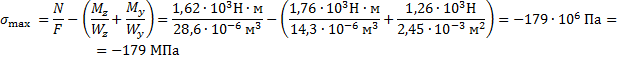4.2 Определение размеров прямоугольного сечения с отношением сторон 1:2 в условиях чистого изгиба

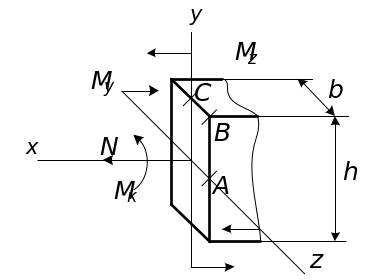
Под чистым изгибом понимается такой вид нагружения, при котором в поперечных сечениях балки возникают только изгибающие моменты, а поперечные силы отсутствуют ( ).

Наиболее нагруженным является поперечное сечение около точки при (см. рис.11).

В этом сечении:

В зависимости от значения , , и соотношения сторон прямоугольного сечения наиболее напряженной точкой в сечении может оказаться одна из трех - A, B и C, как показано на рис.12.

Соотношение сторон:

При подборе размеров поперечного сечения не будем учитывать влияние нормальной силы .

В точке A, посередине длинной стороны сечения, возникает плоское напряженное состояние. По гипотезе наибольших касательных напряжений эквивалентное напряжение в точке А:

Здесь

или

Касательное напряжение в точке максимальное:

	По справочным данным [1] при кручении бруса прямоугольного сечения с соотношением сторон значение коэффициента . Тогда
Рис.12. Сечение звена

Эквивалентное напряжение в точке :

В угловой точке возникает линейное напряженное состояние

В точке , посередине короткой стороны сечения, напряженное состояние плоское.

В данном случае и , поэтому эквивалентное напряжение в точке и вычислять его не будем.

Сопоставление расчетных напряжений в точках и показывает, что наиболее напряженной является точка .

По условию прочности:

Отсюда:

Конструктивно принимаем , тогда .

4.3 Проверка звена на прочность в самой опасной точке

Проверим прочность звена в точке при принятых размерах сторон поперечного сечения с учетом влияния нормальной силы.

Для полученных размеров:

Несмотря на учет влияния нормально силы, расчетное напряжение получилось меньше допускаемого. Это объясняется тем, что конструктивно размеры сечения приняты несколько больше расчетных, а влияние нормальной силы по сравнению с изгибающими моментами чрезвычайно мало.

Недонапряжение:

4.4 Построение эпюр распределения напряжений в поперечном сечении

В наиболее нагруженном сечении с размерами , :

Уравнение нейтральной оси:

Отрезки, отсекаемые нейтральной осью на главных центральных осях поперечного сечения:

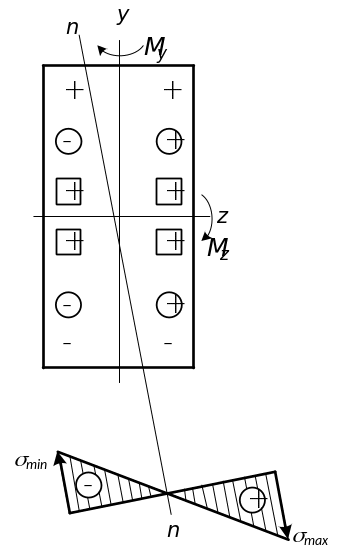
Рис.13. Эпюра напряжений в поперечном сечении

Подставляя числовые значения, получим:

Максимальное напряжение:

Минимальное напряжение:

Эпюра напряжений в сечении изображена на рис.13. На сечении обозначены знаки напряжений: от - знаки обычные, от - знаки, заключенные в кружки, от - в квадратики. Нейтральная линия обозначена как n-n.

5. Выводы

1. При расчете звена получили размеры , , обеспечивающие прочность звена при сложном напряженном состоянии. Т.к. размеры были округлены до целых, то получилось недонапряжение .

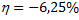2. Расчет показал, что влияние нормальной силы на прочность по сравнению с изгибающими моментами чрезвычайно мало.