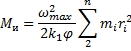4.3 Определение допускаемой глубины поперечной трещины

Максимальные напряжения были определены при подборе размеров поперечного сечения и равны:

Допускаемая глубина поперечной трещины определяется из следующей формулы:

где

- трещиностойкость.

Подставив численные значения, получим:

5. Выводы

1. В результате расчета был выбран профиль двутавровой балки №18, работающий с недонапряжением 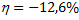. Расчет упругой линии показал, что выбранный двутавр обеспечивает требуемую жесткость балки.

2. Рассчитанные двумя методам (по универсальной формуле упругой линии и по методу Мора) прогиб и угол поворота в середине пролета дали одинаковый результат.

6. Литература

1. Расчетные и курсовые работы по сопротивлению материалов: Учеб. пособие для машиностроит. спец. вузов/Ф.З.Алмаметов, С.И.Арсеньев, Н.А.Курицын, А.М.Мишин. - 2-е изд., перераб. и доп. - М.: Высш. шк., 2003. - 367 с.

2. Феодосьев В.И. Сопротивление материалов: Учеб. для вузов. - 11-е изд., стереотип. - М.: Изд-во МГТУ им. Н.Э.Баумана, 2003. - 592 с.

3. Белявский С.М. Руководство к решению задач по сопротивлению материалов. - 2-е изд., перераб. - М.: Высшкая школа, 1967. - 379 с.

4. Скопинский В.Н., Захаров А.А. Сопротивление материалов: Учебное пособие. Часть I. - М.: МГИУ, 1999. - 128 с.

5. Степин П.А. Сопротивление материалов: Учеб. для немашинотроит. спец. вузов. - 8-е изд. - М.: Высш. шк., 1988. - 367 с.

Звено манипулятора

1. Формулировка задания

Требуется:

• определить размер прямоугольного сечения с отношением сторон 1:2 в условиях чистого изгиба;

• построить эпюры с распределением нагрузок по длине звена и напряжений в поперечном сечении;

• найти самую опасную точку и проверить звено на прочность по теории максимальных касательных напряжений.

Соединение звеньев считать жестким.

2. Расчетная схема

	Рассчитываемое звено: Геометрические характеристики системы: - масса груза - угол поворота поперечное сечение прямоугольное Материал:
Рис.9. Схема манипулятора

3. Предварительные определения

Свойства :

- предел текучести;

- модуль упругости 1-ого рода.

Допускаемые напряжения по пределу текучести:

4. Решение

4.1 Построение эпюр с распределением нагрузок по длине звена

4.1.1 Определение сил, действующих на манипулятор

Нагрузки проистекают из режима работы робота и приходятся на переходный период разгона (торможения) в процессе вращения или качания кисти манипулятора.

Возникающая при этом сила инерции для сосредоточенной массы :

где линейное ускорение:

Касательная и нормальная составляющие:

Линейная скорость, :

где угловая скорость, :

где - угол поворота в радианах.

Таким образом,

После разгона (торможения), когда , .

При разгоне (торможении) с постоянным ускорением:

На участок разгона обычно приходится общего пути поворота , поэтому

Тогда:

Касательная составляющая силы инерции в отличие от нормальной , создает момент относительно оси вращения , который для нескольких сосредоточенных масс:

В манипуляторе главной составляющей является момент от груза с массой и максимальным радиусом вращения . Момент от сил инерции для нескольких сосредоточенных масс рассчитывают через коэффициент конструкции :

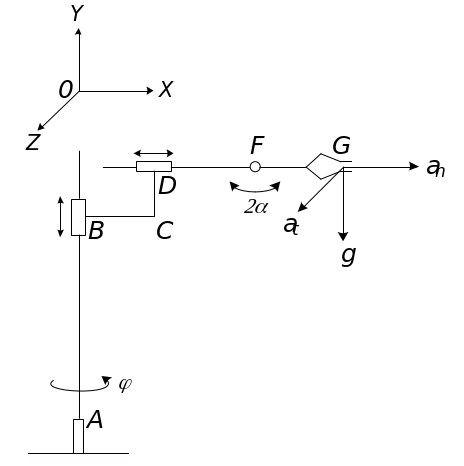
Практика проектирования показывает, что находится в пределах . На этом основании будем вместо массы груза вводить в расчёт эффективное значение массы:

В этом случае можно «закрыть глаза» на массу конструкции, связывающую груз с осью вращения. Подобны образом будем поступать при расчете сил инерции и тяжести .

Т.к. из исходных данных , а соответственно , и между стержнями жесткое закрепление, то звенья и будут представлять собой одно звено с длиной :

Тогда рассчитаем действующие на систему силы:

С учетом действующих сил, заданного угла и условия жесткости соединения звеньев на рис.10 изображена расчетная схема манипулятора.

Рис.10. Расчетная схема манипулятора

4.1.2 Построение эпюр нагрузок

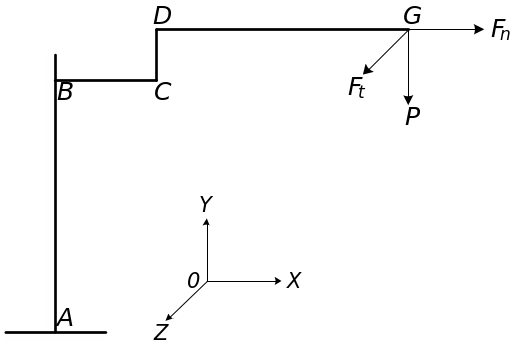
Рассчитываемым звеном является звено . Рассматриваем правую отсеченную часть системы, как показано на рис.11.

Рис.11. Построение эпюр внутренних силовых факторов

Правила знаков:

• нормальную силу считаем положительной, если она вызывает растяжение рассматриваемой отсечено части;

• знаки изгибающих моментов 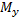и будем определять также как и раньше (балка «плачет» - знак «минус», балка «улыбается» - знак «плюс»);

• крутящий момент считаем положительным, если внешние нагрузки стремятся повернуть отсеченную часть звена по часовой стрелке при взгляде на эту часть со стороны проведенного сечения.

В звене возникает растяжение, кручение и изгиб в двух главных плоскостях и .

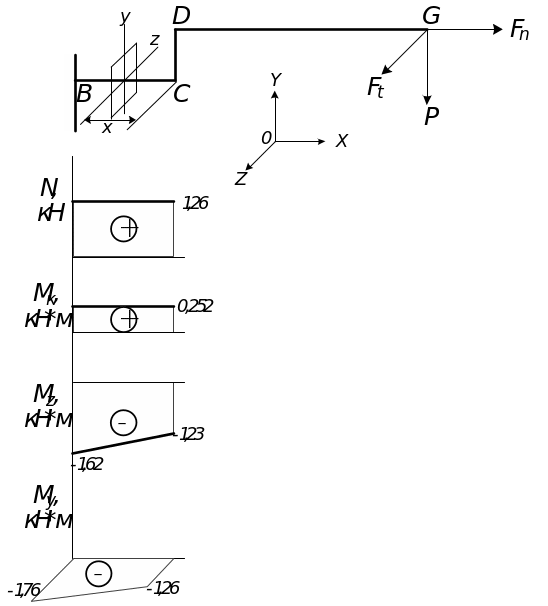
Растяжение:

Кручение:

Изгиб:

По полученным данным строим эпюры внутренних силовых факторов, представленные на рис.11. Ординаты эпюр и можно откладывать в любой плоскости, эпюры изгибающих моментов рекомендуется строить в плоскости их действия, т.е. - в плоскости , а - в плоскости .