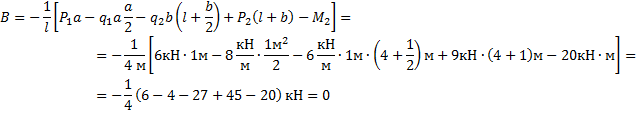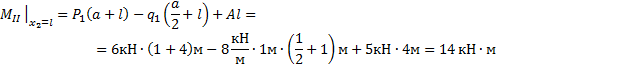Балтийский Государственный Технический Университет «военмех» им. Д.Ф.Устинова Кафедра механики деформируемого твердого тела

ПО - АО - ИТ - Р - ТЛ - НО - З - Г - Б

---------------------------------------------------------------------------------------------------------------------------------

ПРИНЯЛ

профессор (Душин Ю.А.)

Расчетная работа 2

Расчеты на растяжение-сжатие.

Вариант - 8-А; 3a, материал В95; группа Н181, студент Калашников Антон

Выдано 11.11.2010. Срок выполнения 09.12.2010. Представлено

---------------------------------------------------------------------------------------------------------------------------------

Санкт-Петербург

2010

Содержание

Балка 2 3

1. Формулировка задания 3

2. Расчетная схема 3

3. Предварительные определения 3

4. Решение 3

4.1 Определение допускаемых размеров поперечного сечения балки 3

4.2 Построение упругой линии 8

4.3 Определение допускаемой глубины поперечной трещины 18

5. Выводы 18

6. Литература 18

Звено манипулятора 19

1. Формулировка задания 19

2. Расчетная схема 19

3. Предварительные определения 19

4. Решение 19

4.1 Построение эпюр с распределением нагрузок по длине звена 19

4.2 Определение размеров прямоугольного сечения с отношением сторон 1:2 в условиях чистого изгиба 23

4.3 Проверка звена на прочность в самой опасной точке 24

4.4 Построение эпюр распределения напряжений в поперечном сечении 25

5. Выводы 26

6. Литература 26

Балка 2

1. Формулировка задания

Требуется

• определить допускаемые размеры поперечного сечения заданного профиля (швеллер или двутавр по стандарту);

• рассчитать упругую линию, а прогиб и угол поворота сечения в середине пролета проверить альтернативным методом (при досрочной сдаче работы расчет упругой линии по всей длине балки не требуется);

• выяснить допускаемую глубину поперечной трещины.

2. Расчетная схема

   	Сосредоточенные нагрузки: 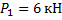; ;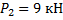 Распределенные нагрузки: ; ; Моменты: 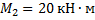; Длины участков балки: 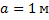; ;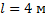 ; 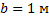Поперечное сечение: двутавр по стандарту; Допускаемые напряжения: 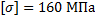; ; Модуль упругости: .
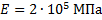   Рис.1. Схема нагружения

3. Предварительные определения

Для углеродистой стали 20: .

4. Решение

4.1 Определение допускаемых размеров поперечного сечения балки

4.1.1. Определение реакций опор.

На основании условий статики ( ):

Слагаемое распределенной нагрузки имеет такой вид, т.к. нагрузка прикладывается к середине участка, на котором она действует.

Знаки определяем так: если действующий момент вращает балку относительно оси шарнира по часовой стрелке, то его считаем положительным, против часовой стрелки - отрицательным.

Подставляя числовые значения, найдем:

Проверка найденных реакций по уравнению равновесия сил ( ):

4.1.2. Построение эпюр и

Правило знаков при построении эпюры:

• изгибающий момент 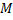считают положительным, если внешние воздействия, расположенные по любую сторону от сечения, изгибают балку в области этого сечения выпуклостью вниз. Иначе говоря, момент считают положительным, если при его действии в заданном сечении балка «улыбается»;

• поперечную силу 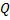считают положительной, если равнодействующая внешних сил по любую сторону от сечения вращает отсеченную часть балки относительного этого сечения по часовой стрелке.

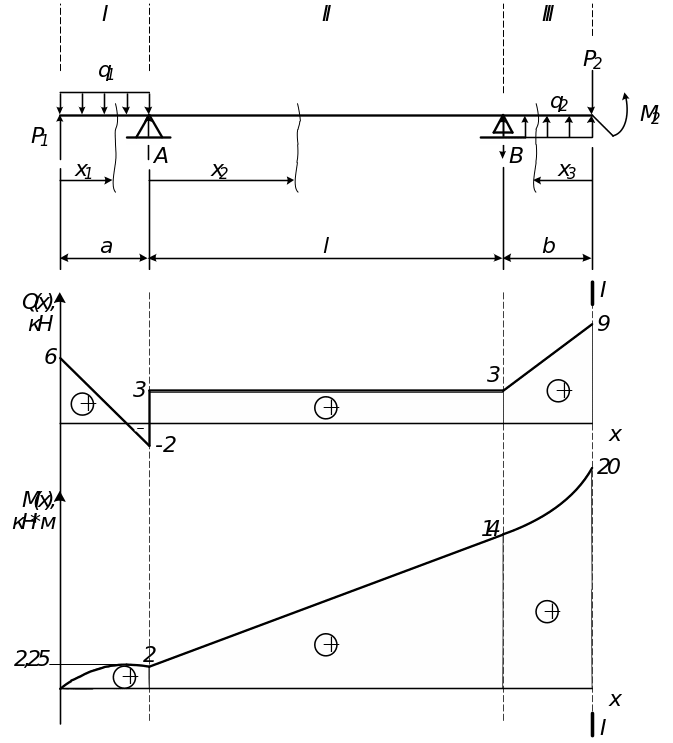
Балку разбиваем на три участка, где каждый новый участок соответствует появлению новой силы или нового момента, как показано на рис.2.

На участке :

Т.к.

то, приравняв (т.е. первую производную к нулю), найдем экстремум функции :

На участке :

Рис.2. Эпюры силы и момента

На участке :

Определяем точку экстремума:

По полученным результатам строим эпюры и , представленные на рис.2.

4.1.3. Подбор размеров поперечного сечения

По эпюре изгибающего момента видно, что наибольший момент возникает в сечении (рис.2). По условию прочности на нормальные напряжения:

Следовательно, момент сопротивления, удовлетворяющий условию прочности:

По ГОСТ 8239-72 ближайшие по моменту сопротивления двутавровые балки:

• двутавр №16: ;

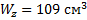• двутавр №18: .

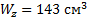Проверяем двутавр №16.

Для него максимальные напряжения:

Перенапряжение:

Такое перенапряжение недопустимо.

Проверяем двутавр №18.

Максимальные напряжения:

Недонапряжение:

Принимаем двутавр №18, для которого:

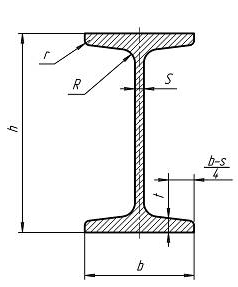
Рис.3. Двутавровая балка

4.1.4. Проверка прочности на касательные напряжения

Наибольшая по абсолютной величине поперечная сила возникает в сечении (рис.2). Поэтому максимальные касательные напряжения, возникающие в сечении, определятся по формуле Журавского:

где

- статический момент части площади поперечного сечения , расположенной выше (или ниже) рассматриваемой точки относительно нейтральной оси , равный произведению этой площади на расстояние центра тяжести этой площади до оси ;

- ширина поперечного сечения в опасной точке (обычно на нейтральной оси);

- момент инерции всей площади поперечного сечения относительно нейтральной оси .