1.Предмет кинематики. В кинематике изучаются геометрические законы механического движения материальных тел без учета их масс и причин, вызывающих это движение. Основная задача кинематики точки состоит в том, чтобы по заданному закону движения точки найти ее основные кинематические характеристики: траекторию, скорость и ускорение. Траектория - непрерывная линия, которую описывает движущаяся точка (если траекторией является прямая линия – движение прямолинейное; кривая – криволинейное). За единицу длины принят 1м, а за единицу времени 1с. В задачах кинематики время t принимают за независимую переменную (аргумент). Все другие переменные (расстояние, скорость, ускорение) рассматриваются как изменяющиеся с течением времени, т.е. как функции времени t.

2. В зависимости от выбора системы отсчета существует три способа задания движения точки: векторный, координатный и естественный. Векторный. В векторном способе задания движения точки ее положение в любой момент времени определяют радиусом-вектором r=вектору OM, проведенным из начала координат O в движущуюся точку M (рис.1), то есть векторной функцией Координатный. В координатном способе задания движения точки положение точки в любой момент времени определяется зависимостями ее декартовых координат от времени x=f1(t); y=f2(t); z=f3(t) . Эти уравнения представляют собой уравнения движения точки в координатной форме. Они одновременно являются уравнениями траектории в параметрической форме, в которых роль параметра выполняет время t. Естественный. Применяется в том случае, когда траектория движения точки известна. В каждой точке известен радиус кривизны траектории p(ро). Если кривая AB является траекторией точки M, то положение точки M на этой траектории можно однозначно определить криволинейной координатой s. Координата s отсчитывается от некоторой фиксированной точки (начало отсчета) вдоль траектории и берется с соответствующим знаком. Чтобы знать положение точки M на траектории в любой момент времени, надо задать зависимость криволинейной координаты от времени 0M . s = s(t) . (1.9) Уравнение (1.9) выражает закон движения точки при естественном способе задания ее движения. Отметим, что величина s в общем случае не равна пройденному точкой пути.

3. Скорость и ускорение точки при векторном и координатном способах задания движения точки. При векторном. Скоростью точки называют вектор v, равный первой производной по времени t от ее радиуса-вектора r, то есть от векторной функции : = или (1.2) Вектор скорости направлен по касательной к траектории точки в сторону ее движения. Ускорением точки называется вектор a, равный первой производной по времени t от ее скорости v или второй производной от ее радиуса-вектора r: или . При криволинейном движении точки в плоскости Oxy ускорение расположено в этой плоскости и отклонено от скорости в сторону вогнутости траектории точки. При прямолинейном движении точки векторы скорости и ускорения направлены вдоль траектории в одну сторону или противоположные стороны.

3 и 5 вопрос. При координатном. Модуль скорости v и ее направляющие косинусы определяются формулами: . (углы , вектор v образует с координатными осями.) Модуль ускорения a и его направляющие косинусы определяются по формулам:

В случае прямолинейного движения, которое задается одним уравнением x=f(t), скорость и ускорение точки будут:

4. Проекции скорости и ускорения на координатные оси. На основании формулы (1.2) проекции скорости точки равны первым производным по времени от соответствующих координат точки: . Проекции ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени:

или

6. Чтобы получить уравнение траектории надо из уравнений движения исключить параметр t.

7. Скорость и ускорение при естественном способе задания движения. Из курса высшей математики известно, что . Разделим это на и получим: ; отсюда -единичный вектор касательной или орт касательной -модули орт векторов. Вектор ускорения точки расположен в соприкасающейся плоскости и раскладывается на две взаимно перпендикулярные составляющие, одна из которых направлена по касательной к траектории точки, а вторая – по главной нормали к этой траектории в сторону вогнутости: Ускорение точки. Составляющая ускорения в направлении бинормали равна нулю . Если направлены одинаково, то v-увеличится, движение точки умеренное. Если они направлены противоположно, то v уменьшается, движение точки замедленное. Если

или

8. Касательные и нормальные составляющие ускорения точки. Составляющие вектора ускорения называют касательным (тангенциальным) и нормальным ускорениями. По состовляющим можно определить модуль ускорения:

9. радиус кривизны траектории в данной точке – это радиус такой окружности, с элементарной дугой которой совпадает участок криволинейной траектории в малой окрестности той точки, где находится движущаяся материальная точка.

10.Частные случаи движения точки. Равномерное: это движение точки с постоянной алгебраической скоростью, при котором . Ускорение в случае равномерного криволинейного движения точки равно нормальному ускорению . При прямолинейном равномерном движении ускорение равно нулю, т.к. Равнопеременное: это движение точки с постоянным по модулю касательным ускорением. . Постоянные интегрирования (C, S-направление отсчета координаты

11. При поступательном движении твердого тела отрезок прямой соединяющий любые 2 точки тела, перемещается параллельно самому себе. При этом все точки тела движутся по одинаковым траекториям и в момент времени t имеют одинаковые скорости и ускорения. Поступательное движение твердого тела вполне определяется движением какой-нибудь одной его точки. Следовательно, изучение поступательного движения тела сводится к уже рассмотренной задаче кинематики точки.

12. Вращение твердого тела вокруг неподвижной оси. Вращательным называется такое движение твердого тела, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во время движения неподвижными. При этом также остаются неподвижными все точки тела, расположенные на прямой, проходящей через эти точки. Это прямая называется осью вращения тела. -закон вращения тела [радианы] ;

13. Закон движения. Зависимость всех координат тела от времени называется законом движения, то есть закон движения определяет положение тела в любой произвольный момент времени.

14. Угловая скорость и ускорение тела. Производная по времени от угла поворота называется угловой скоростью, которая показывает как быстро и в каком направлении вращается тело [рад/с или ]. . Производная по времени от угловой скорости называется угловым ускорением, которое характеризует быстроту изменение угловой скорости твердого тела: [рад\ или ]. Если , то в данный момент вращение тела называется ускоренным. Если знаки разные, то замедленным.

15. Скорость и ускорение точки вращающегося тела. Согласно закону все точки вращающего тела описывают окружности. Например, траекторией точки А является окружность радиуса . При повороте тела на угол точка А перемещается по дуге окружности на . Скорость точки А определяется по формуле А определяется по формуле . Вектор скорости направлен по касательной к окружности в направлении поворота тела. Таким образом, числовое значение скорости точки вращающегося тела равно произведению угловой скорости тела на расстояние от этой точки до оси вращения.

16. Равномерное вращение твердого тела. Уравнение равномерного вращения имеет вид / В частном случае, когда начальный угол поворота =0, = .Угловая скорость , можно выразить и так: ω = 2π/T, где T – период вращения тела; φ=2π – угол поворота за один период.

17. Связь. Между углом поворота и числом оборотов: Угол поворота выражается в радианах. Иногда угол поворота определяется числом оборотов N. Зависимость между и N следующая . между частотой вращения и угловой скоростью: в технике часто скорость вращения тела задают частотой вращения n, т.е. числом оборотов, совершаемых телом за одну минуту. Найдем зависимость между n об\мин и При одном обороте тело повернется на угол 2 , а при n оборотах на ; этот поворот совершается за время t=1мин=60с. Тогда

18.Угловая скорость и закон равнопеременного вращения тела. Вращение с постоянным угловым ускорение называется равнопеременным. Проинтегрировав равенство , получаем . Закон равнопеременного вращения

19.Аксиомы статики. 1.Система двух равных по величине, но противоположно направленных по одной линии и приложенных к одному телу сил, эквивалентно нулю.

, ,

А Тело находится в равновесии

2.Механическое состояние тела не изменится, если к системе сил добавить или изъять из нее систему сил, эквивалентную нулю. Имеем систему сил и имеется уравновешенная система сил , то 3. Всякое действие вызывает равное и прямо противоположное противодействие. Эту аксиому в динамике называют третьим законом Ньютона о равенстве действия и противодействия.

Тело S действует на тело Q в точке А силой Р, а тело Q на S силой N.В соответствии с аксиомой силы равны по модулю P=N, но противоположны по направлению . В данном случае силы приложены к разным телам, поэтому первая аксиома здесь неприминима. P-вес тела. N-сила противодейс

n

S

A

Q

4

. Все три силы находятся в одной плоскости. Величину равнодействующей можно найти графически как длину диагонали параллелограмма или вычислить по теореме косинусов:

. 2 силы приложенные в одной точке (аксиома о сложении двух сил). Система двух сил , приложенных в одной точке твердого тела, всегда имеет равнодействующую силу

Данная аксиома допускает и обратное утверждение: силу можно разложить бесчисленным множеством способов на две силы.

20. Сила является основной мерой механического взаимодействия материальных тел. Это величина векторная и определяется числовым значением (модулем), направлением и точкой приложения. За единицу измерения силы в системе СИ принят 1Н. Сила, величиной 1Н, приложенная к покоящемуся телу массой 1кг, вызывает движение тело с ускорение 1м/ . Линия по которой направлена сила, называется линией действия силы.

21.Классификация систем сил. Совокупность нескольких сил, действующих на данное тело или систему тел, называется системой сил. –плоская система сил – если линии действия всех сил лежат в одной плоскости. –пространственная – линии действия сил не лежат в одной плоскости. –сходящаяся – линии действия пересекаются в данной точке. –параллельные – линии действия параллельны друг другу. –эквивалентные – две системы сил вызывают у одного и того же тела одинаковое кинематическое состояние. (Твердое тело может находиться в состоянии покоя или некоторого движения. Каждое из этих состояний является кинематическим состоянием тела.) - если система сил , то сила равнодействующей данной системы сил. –уравновешенная – если система сил, будучи приложенной к телу, не изменяет его кинематического состояния. Уравновешенная система сил эквивалентна нулю: -силы, действующие на части объема, поверхности или линии, называются распределенными. Эти силы характеризуются интенсивностью q,т.е. значением силы, приходящейся на единицу объема (в случае объемных сил), на единицу площади (в случае поверхностных сил), на единицу длины (в случае действия сил по линии).

22.Проекция силы на ось и плоскость. Проекция силы на ось равна произведению модуля силы на косинус угла между положительным направлением оси и направлением проектируемой силы: ), . Если угол между положительным направлением оси и вектором силы заключен в переделах от , то проекция силы на ось положительна, а если от , то проекция отрицательна. Если перпендикулярна оси, то ее проекция на эту ось равна нулю. Например, для данных сил, проекциями сил на оси х, у будут:

y

стр 15

Проекцией силы на плоскость называется вектор , заключенный между проекциями начала и конца силы на эту плоскость. -проекция силы на плоскость . , ; -модуль силы.

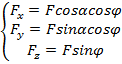
2 3.Сложение сходящихся сил. При векторном способе сложения сходящихся сил (геометрический способ) равнодействующая системы сил приложенная в той же точке О я является замыкающей стороной силового многоугольника, построенного на слагаемых силах.(2 рисунок)

При построении силового многоугольника нужно к концу F1 присоединить параллельно перенесенный F2, а к нему F3 и т.д.Данный способ сложения является простым и наглядным. Однако точность определения зависит от точности построения силового многоугольника. Аналитический способ сложения сходящихся сил, который называют способом проекций. Спроектируем силы на горизонтальную ось и алгебраически сложим их проекции: od=oa+ab-bc+cd. Проекцией равнодействующей R сходящихся сил на горизонтальную ось будет отрезок od. -модуль R Направление равнодействующей определяется через ее направляющие косинусы ) , ) , cos(z ^

24. Разложение силы. -разложение силы на составляющие. всякую силу можно разложить на горизонтальную и вертикальну составляющие, построив прямоугольник, для которого эта сила была бы диагональю. Горизонтальная и вертикальная стороны прямоугольника дадут горизонтальную и вертикальную составляющие силы соответственно. (И наоборот, если две силы приложены в одной точке, то, построив параллелограмм, двумя смежными сторонами которого являются эти две силы, можно найти их равнодействующую как диагональ параллелограмма.)

2 5.Равновесие сходящихся сил. . Ее модуль , следовательно . Таким образом, для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнялись нулю суммы проекций всех сил на оси координат.

2

Будет ли находиться балка в равновесии или вращаться вокруг точки о? чтобы ответить на этот вопрос нужно ввести момент силы относительно центра.

6

с тр 19

Момент силы относительно центра О называется вектор, равный векторному произведению радиус-вектора , проведенного из центра О в точку А, где приложена сила, на вектор силы : .Из определения векторного произведения следует, что вектор направлен перпендикулярно плоскости OAB, образованной векторами r и F, в ту сторону, откуда мы видим направление силы F против хода часовой стрелки. Модуль вектора момента равен , где sin -плечо силы относительно центра О, т.е. кратчайшее расстояние от центра О до линии действия силы . Момент силы относительно точки О есть взятое со знаком плюс или минус произведение модуля силы на кратчайшее расстояние от точки О до линии действия силы: )= Момент является положительным, если сила стремится повернуть тело относительно точки против хода часовой стрелки. Два свойства для момента силы относительно точки: 1.Момент силы относительно точки равен нулю, если эта точка находится на линии действия силы. 2.Момент силы относительно точки не изменится, если силу как скользящий вектор перенести вдоль линии действия. Например если точку приложения А силы F перенести в точку С. Балка AB будет оставаться в горизонтальном положении (равновесии), если момент силы относительно точки О будут уравновешены: Из уравнения можно определить величину уравновешивающей (не равнодействующей!) силы

2 7.Пара сил - система двух равных по модулю, параллельных и противоположно направленных сил . Плоскость, в которой находятся линии действия сил , называется плоскостью действия пары сил. Расстояние d=AB между линиями действия сил - плечо пары сил. Пара сил стремится повернуть тело в плоскости действия сил.

Пара сил не имеет равнодействующей, однако силы пары не уравновешиваются , т.к. они не направлены по одной прямой.

28. Момент пары равен произведению модуля одной из сил пары на ее плечо: . Момент пары можно представить в виде вектора , направленного перпендикулярно плоскости действия пары сил, это свободный вектор. Свободный вектор можно переносить в пространстве как угодно, не меняя направление. Например, если вектор m перенести вдоль линии действия, пара сил переносится в параллельную плоскость, а если вектор перенести параллельно, то пара сил переносится в плоскости действия пары сил. Если на тело действуют несколько пар с моментами . Этот результата выражает , теорему о сложении пар.

29. Связи и их реакции. Все то, что ограничивает перемещение называется связью. Сила, препятствующая со стороны связи тем или иным его перемещениям, называется силой реакции (противодействия) связи или просто реакцией связи. 1.Гладкая поверхность – если можно пренебречь силами трения между телами.

Гладкая поверхность не позволяет перемещаться телу по направлению к нормали к поверхностям тел в точках их касания. Поэтому рекции будут направлены по нормалям и приложены в точках взаимодействия.