Выполнение:

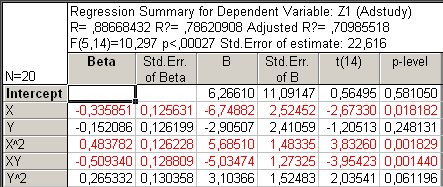
Рис27. Регрессионный анализ всех независимых переменных

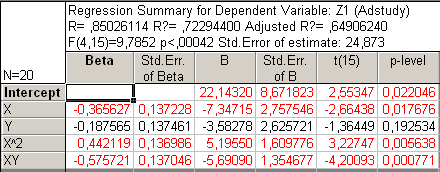
Рис28. Регрессионный анализ без У²

Рис29. Регрессионный анализ без ХУ

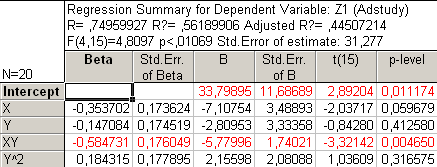
Рис30. Регрессионный анализ без X²

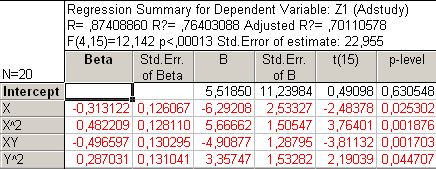
Рис31. Регрессионный анализ без У

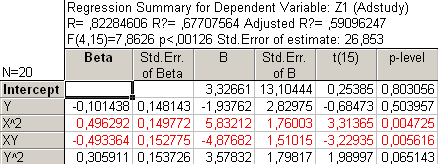
Рис32. Регрессионный анализ без Х

Рис33. Регрессионный анализ без ХУ и У²

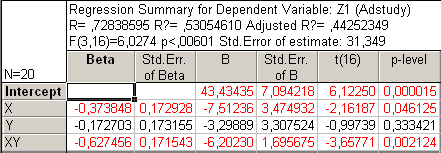
Рис34. Регрессионный анализ без Х² и У²

Рис35. Регрессионный анализ без У² и У

Рис36. Регрессионный анализ без У² и Х

Рис37. Регрессионный анализ без ХУ и Х²

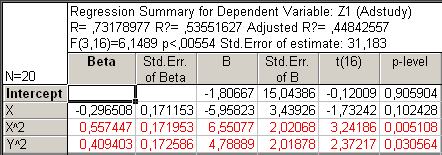
Рис38. Регрессионный анализ без ХУ и У

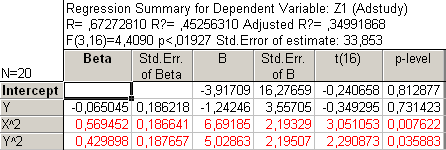
Рис39. Регрессионный анализ без ХУ и Х

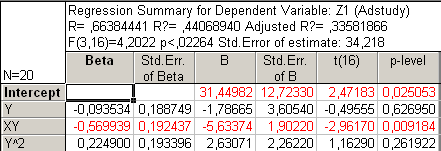
Рис40. Регрессионный анализ без Х и Х²

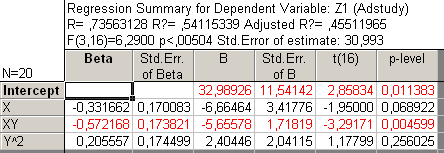
Рис41. Регрессионный анализ без У и Х²

Рис42. Регрессионный анализ без Х и У

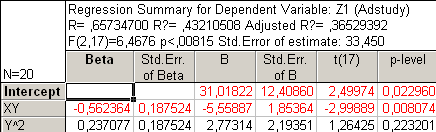
Рис43. Регрессионный анализ без Х, У и Х²

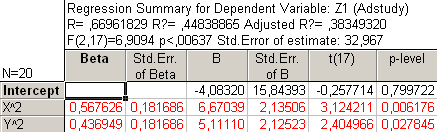
Рис44. Регрессионный анализ без Х, У, ХУ

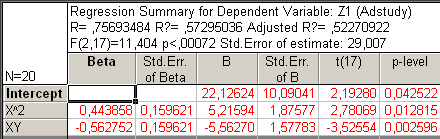
Рис45. Регрессионный анализ без Х,У и У²

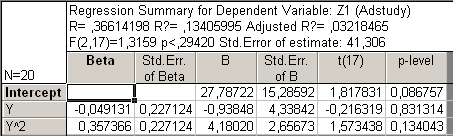
Рис46. Регрессионный анализ без Х, Х² и ХУ

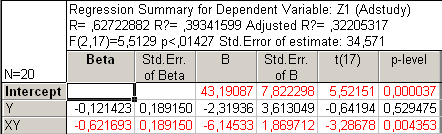
Рис47. Регрессионный анализ без Х, Х² и У²

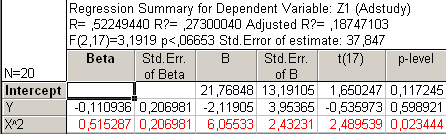
Рис48. Регрессионный анализ без Х, ХУ и У²

Рис49. Регрессионный анализ без У, ХУ, У²

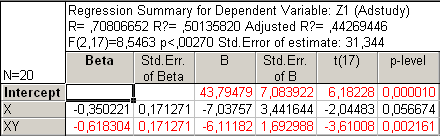
Рис250. Регрессионный анализ без У, Х², У²

Рис51. Регрессионный анализ без У, Х², ХУ

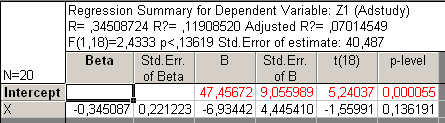
Рис52. Регрессионный анализ с Х

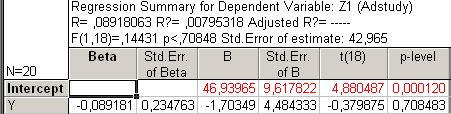
Рис53. Регрессионный анализ с У

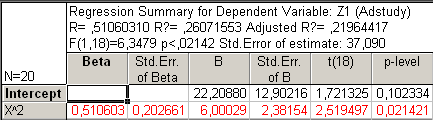
Рис54. Регрессионный анализ с Х²

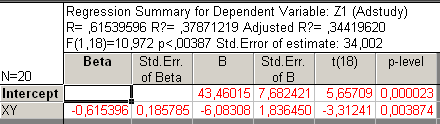
Рис55. Регрессионный анализ с ХУ

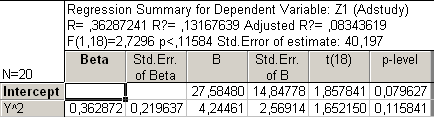
Рис56. Регрессионный анализ с У²

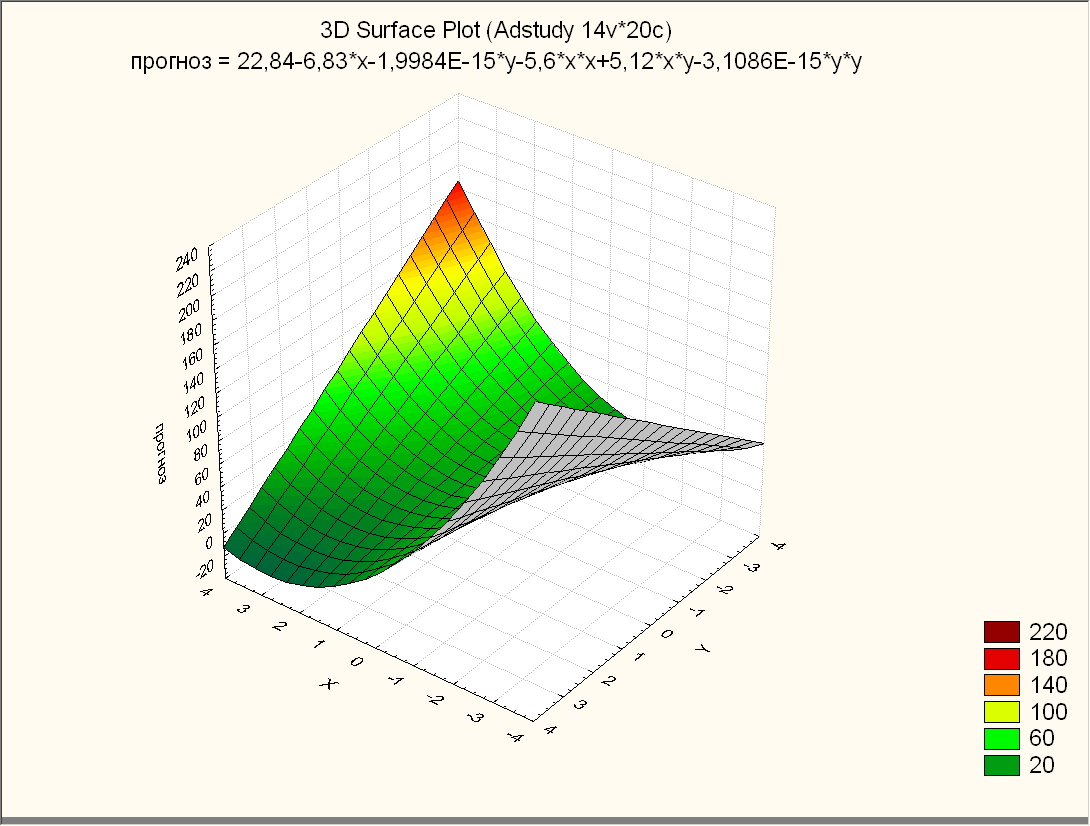
Рис57. Трехмерный график, виден минимум

Рис58. Контурный график.

Вывод: Из всех различных регрессионных анализов (рис35, рис45 и рис56) выбираем тот, у которого коэффициент детерминации ( ) выше, чем у остальных и ошибка прогноза выработки (S) наименьшая.

Выбираем регрессионный анализ без У² и У (рис35) с данными:

=0,63 и S=25,534

И получаем функцию: f=22,84-6,834х+5,1219х²-5,6ху

Построены трехмерные графики данной функции, на которых виден минимум.