
1.3.Нелинейная зависимость
Задание: Имеются эмпирические данные о зависимости y - выработки на одного работника доменного производства от x - температуры дутья; данные приведены в табл. 3 в условных единицах.
Таблица 3
№ |
X |
Y |
№ |
X |
Y |
1 |
1.01 |
8.8 |
11 |
5.80 |
11.8 |
2 |
1.15 |
9.2 |
12 |
6.14 |
12.2 |
3 |
1.91 |
8.7 |
13 |
6.64 |
13.1 |
4 |
2.47 |
10.2 |
14 |
6.85 |
14.4 |
5 |
2.66 |
9.3 |
15 |
8.11 |
17.5 |
6 |
2.74 |
9.4 |
16 |
8.47 |
18.6 |
7 |
2.93 |
10.7 |
17 |
9.09 |
18.6 |
8 |
4.04 |
8.5 |
18 |
9.23 |
18.0 |
9 |
4.50 |
8.9 |
19 |
9.59 |
23.8 |
10 |
4.64 |
8.0 |
20 |
9.96 |
18.4 |
Выполнение:
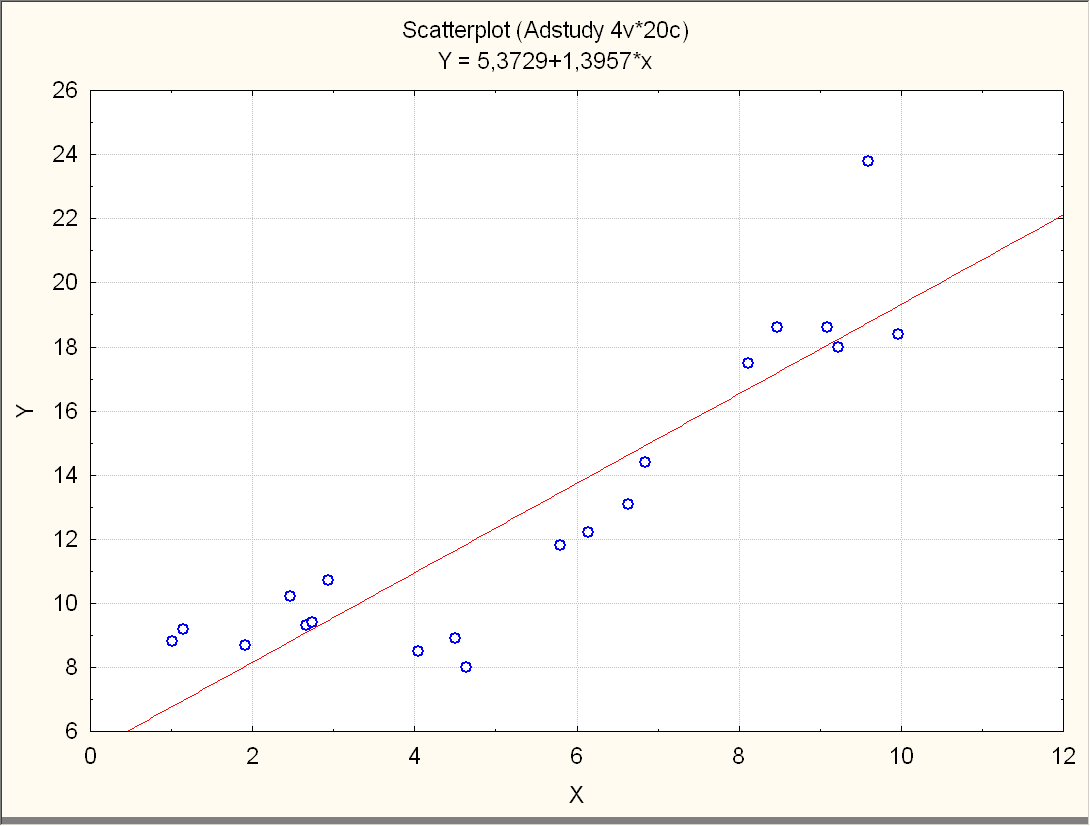
Рис22. Диаграмма рассеяния
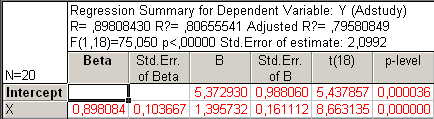
Рис23. Регрессионный анализ первой степени: y = о + 1 x
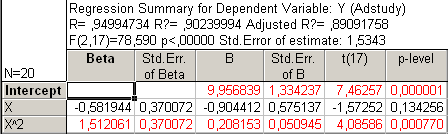
Рис24. Регрессионный анализ второй степени: y = о + 1 x + 2 x2
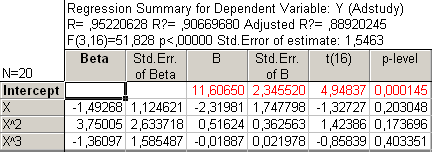
Рис25. Регрессионный анализ третьей степени: y = о + 1 x + 2 x2 + 3 x3
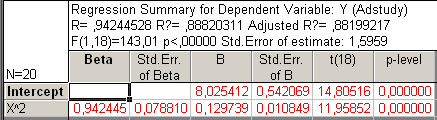
Рис26. Регрессионный анализ без линейного члена: y = о + 2 x2
Вывод: Из регрессионного анализа первой степени получаем:
y = 5.36 + 1.40 x
![]() = 0.798, s
= 2.09.
= 0.798, s
= 2.09.
Из регрессионного анализа второй степени получаем:
y = 9.9 - 0.88 x + 0.21 x2
= 0.892, s = 1.53
Данная регрессия лучше предыдущей, т.к. =0.892 больше чем = 0.798 и s меньше, чем в первом случае.
Из регрессионного анализа третьей степени получаем:
y = 11.6 - 2.35 х + 0.53 х2 - 0.02 х3
= 0.890, s = 1.53
Поскольку степень увеличилась без увеличения , от регрессии третьей степени отказываемся в пользу второй степени.
Из регрессионного анализа без линейного члена получаем:
y = 8.02 + 0.13 x2
= 0.884, s = 1.6
Сравнивая ее по и s со второй степенью, отдаем предпочтение второй, поскольку ошибка прогноза s меньше. Делаем вывод, что регрессионный анализ второй степени более предпочтителен.
1.4.Нелинейная зависимость (обобщение)
Задание: Имеется 20 наблюдений по некоторому технологическому процессу химического производства; x, y - изменяемое содержание двух веществ , z - контролируемый параметр получаемого продукта. Полагая, что
z = P (x, y) + ,
где P (x, y) = о + 1 x + 2 y + 3 x2 + 4 xy + 5 y2 - многочлен второй степени, - случайная составляющая, М = 0, D = 2, необходимо оценить функцию P(x, y) и найти точку ее минимума. Данные приведены в табл. 4.
Таблица 4
i |
xi |
yi |
1 zi |
2 zi |
3 zi |
4 zi |
5 zi |
6 zi |
7 zi |
8 zi |
1 |
-3 |
-2 |
68 |
222.3 |
260 |
17.1 |
168 |
122.3 |
160 |
117.1 |
2 |
-3 |
1 |
89.4 |
146.8 |
161.4 |
114.8 |
189.4 |
46.8 |
61.4 |
214.8 |
3 |
-3 |
3 |
148.5 |
155.4 |
60.5 |
155.4 |
248.5 |
55.4 |
0.5 |
255.4 |
4 |
-2 |
-3 |
56.8 |
205.2 |
248.8 |
7.7 |
156.8 |
105.2 |
148.8 |
107.7 |
5 |
-2 |
0 |
18.5 |
148.4 |
186.5 |
116.4 |
118.5 |
48.4 |
86.5 |
216.4 |
6 |
-2 |
2 |
73 |
145.5 |
145 |
145.5 |
173 |
45.5 |
45 |
245.5 |
7 |
-1 |
-2 |
29.2 |
141.4 |
221.2 |
53.6 |
129.2 |
41.4 |
121.2 |
153.6 |
8 |
-1 |
3 |
46 |
175.1 |
118 |
143.1 |
146 |
75.1 |
18 |
243.1 |
9 |
0 |
-3 |
46.2 |
134 |
174.2 |
60.9 |
146.2 |
34 |
74.2 |
160.9 |
10 |
0 |
-1 |
18.2 |
100.6 |
210.2 |
94 |
118.2 |
0.6 |
110.2 |
194 |
11 |
0 |
2 |
31.6 |
118.5 |
199.6 |
86.5 |
131.6 |
18.5 |
99.6 |
186.5 |
12 |
1 |
-1 |
8.6 |
108.4 |
207.9 |
94.5 |
108.6 |
8.4 |
107.9 |
194.5 |
13 |
1 |
1 |
8.4 |
121.3 |
194.5 |
89.3 |
108.4 |
21.3 |
94.5 |
189.3 |
14 |
1 |
3 |
1.9 |
189.4 |
215.4 |
61.4 |
101.9 |
89.4 |
115.4 |
161.4 |
15 |
2 |
-3 |
122.3 |
107.5 |
117.1 |
112.2 |
222.3 |
7.5 |
17.1 |
212.2 |
16 |
2 |
1 |
8.1 |
125.8 |
205.4 |
53.8 |
108.1 |
25.8 |
105.4 |
153.8 |
17 |
2 |
-3 |
20.8 |
205.9 |
186.9 |
5.9 |
120.8 |
105.9 |
86.9 |
105.9 |
18 |
3 |
-2 |
105.2 |
120.8 |
107.7 |
86.9 |
205.2 |
20.8 |
7.7 |
186.9 |
19 |
3 |
0 |
34 |
133 |
160.9 |
61 |
134 |
33 |
60.9 |
161 |
20 |
3 |
2 |
7.5 |
200.4 |
212.2 |
0.4 |
107.5 |
100.4 |
112.2 |
100.4 |
