
- •Тема №5. Элементы общей теории волноводов
- •5.2. Решение волновых уравнений для направляемых волн
- •6.1. Эмп в прямоугольном волноводе. Определение продольных и
- •6.1.1. Определение продольных компонент поля
- •Волна типа ē
- •6.1.2. Определение поперечных компонент поля
- •Выражения для компонент поля в вещественной форме
- •6.2. Диаграмма типов волн. Основная волна прямоугольного волновода и ее структура.
- •6.2.1. Диаграмма типов волн. Основная волна прямоугольного волновода
- •6.2.2. Методика построения структуры волн в прямоугольном волноводе
- •3.3. Структура волн высших типов.
- •Волна н11□
- •Волна e11□
- •3.4. Устройства связи линии передачи с нагрузкой
- •Тема №7. Круглые волноводы и волноводы специального сечения
- •7.1. Эмп в круглом волноводе
- •Тема №8. Объемные резонаторы.
- •8.2.2. Объемные резонаторы волноводного типа со стоячей волной.
- •8.2.3. Добротность объемного резонатора
- •8.2.4. Структура полей в резонаторах волноводного типа.
- •Тема №9. Элементы техники свч.
- •Структурный состав типового волноводного тракта.
- •9 .2. Волноводные тройники
- •9.3. Частотные фильтры.
- •9.4. Фильтры типов волн.
- •9.5. Волноводные соединения, изгибы, скрутки, вращающиеся сочленения,
- •9.6. Мостовые схемы свч.
- •9.6.1. Двойной волноводный тройник.
- •9.6.2. Волноводно-щелевой мост.
- •9.6.3. Кольцевой волноводный мост.
- •9.7. Направленные ответвители.
- •9.8. Волноводные устройства с ферритами.
- •9.9. Антенные переключатели.
- •Раздел №2. Распространение радиоволн. Тема №1. Область пространства существенная для распространения радиоволн.
- •Диапазоны радиоволн. Факторы, влияющие на ррв.
- •1.2. Понятие о зонах радиосвязи (видимости) рэт.
- •1.3. Принцип Гюйгенса-Френеля. Область пространства, существенная для ррв. Зоны Френеля
- •1.4. Принцип отражательной трактовки. Участок поверхности, существенный при отражении рв.
- •1.5. Отражение радиоволн при горизонтальной и вертикальной поляризации. Интерференционный множитель Земли.
- •Учет рельефа местности и влияния кривизны Земли. Дальность прямой видимости.
- •Тема №2. Ррв в тропосфере.
- •. Общие сведения о тропосфере. Понятие нормальной тропосферы и
- •Ослабление энергии радиоволн тропосферой и его учет в радиолокации и радиосвязи. Ослабление рв
- •Рассеяние радиоволн на неоднородностях тропосферы. Дальнее
- •Тема №3. Ррв в ионосфере.
- •3.1. Общие сведения о физике ионосферы. Образование ионизированных слоев атмосферы. Простой ионосферный слой.
- •3.2. Особенности реальной ионосферы. Эффекты ррв в ионосфере.
- •3.3 Электрические параметры ионосферы. Плазменная частота.
Тема №5. Элементы общей теории волноводов
5.1. Линии передачи СВЧ.
5.1.1. Классификация линий передачи.


симметричные кабели
Волноводы(5.3 а) –диэлектрические. (5.3б)- полый волновод.

Волноводы специального сечения. (5.а) (в –коаксиал)(г- Двухпроводные линии открытого и закрытого типов)

Если волновод одного сечения и не имеет изгибов, заполнен однородным диэлектриком –однородный регулярный(5.4а). 5.4б-одродный нерегулярный(имеет изгиб). Иногда ставят кварцевые стекла и нагнетают воздух под давлением , для исключения попадания частиц 5.4(в).

5.1.2. Классификация направляемых волн.
Н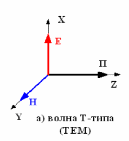 е
имеет продольных составляющих векторов
E и H.
е
имеет продольных составляющих векторов
E и H.
Распространяется в коаксиальном кабеле.


Имеет продольную составляющую вектора E. Имеет продольную составляющую вектора H.
В олна
типа T в волноводах не распространяется.
олна
типа T в волноводах не распространяется.
Первый закон Максвелла:

Так как волновод полый, проводимость равно 0:

Ток смещения
совпадает по направлению с электрическим
полем, но отличается по фазе на .
Следовательно для того чтобы волна
распространялась продольная составляющая
.
Следовательно для того чтобы волна
распространялась продольная составляющая
 .
.
5.2. Решение волновых уравнений для направляемых волн
Постановка задачи
Пусть мы имеем регулярный, однородный, волновод.
S = const-поперечное сечение.

 отсутствуют
источники тока.
отсутствуют
источники тока.
 Любой момент
времени.
Любой момент
времени.
Методика решения
Запишем уравнения Максвелла и наши условия:

Метод непосредственного получения векторов (векторные однородные уравнения Даламбера)

Метод разделения переменных.
E и H представляют собой функции:
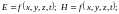 представим в виде
поперечных и продольных составляющих:
представим в виде
поперечных и продольных составляющих:
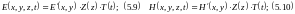
 -векторные функции
распределения поля в поперечном сечении.
-векторные функции
распределения поля в поперечном сечении.
Временная
зависимость:
 -коэффициент
распространения.”-“ т.к волна
распространяется.
-коэффициент
распространения.”-“ т.к волна
распространяется.
Подставим в (5.9) и (5.10) соответственно:

Распишем продольную и поперечную составляющие:

Подставим(5.13
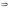 5.11
5.8
и 5.14
5.12
5.7)
получим:
5.11
5.8
и 5.14
5.12
5.7)
получим:

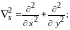 -оператор
Лапласа.
-оператор
Лапласа. -собственное
число мембранных(дисперсионных)
уравнений.
-собственное
число мембранных(дисперсионных)
уравнений.
Для начала решаются скалярные уравнения, а т.к. они подобны, результат применим к векторным, также применим граничные условия.
Решаем (5.16) и (5.19),
подставляем граничные условия.
 -замыкается
на стенках волновода.
-замыкается
на стенках волновода.
 параллелен
стенкам волновода.
параллелен
стенкам волновода.
исследуем функцию
на максимум
П
 олучили
продольные составляющие. Используем
их для получения продольных составляющих.
Для этого будем использовать выражения
связывающие поперечные и продольные
составляющие, которые выводятся из
уравнений Максвелла.
олучили
продольные составляющие. Используем
их для получения продольных составляющих.
Для этого будем использовать выражения
связывающие поперечные и продольные
составляющие, которые выводятся из
уравнений Максвелла.
В итоге мы получили решение с учетом граничных условий.

5.3. Параметры волнового процесса в волноводах.
5.3.1. Постоянная распространения и критическая длина волны (частота)
Постоянная распространения:
 возможны 3 варианта
возможны 3 варианта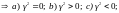
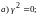


 волновой
множитель, т.к
волновой
множитель, т.к
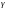 ,
,
 ,
фаза не зависит от расстояния, волнового
процесса в волноводе нет, электромагнитная
энергия не передается, колеблется между
стенками волновода.
,
фаза не зависит от расстояния, волнового
процесса в волноводе нет, электромагнитная
энергия не передается, колеблется между
стенками волновода.



Коэффициент затухания можем определить:

Волновой множитель
 волновой процесс очень быстро затухает,
можно считать что его нет.
волновой процесс очень быстро затухает,
можно считать что его нет.
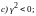

Волновой множитель
 волновой процесс есть, волна
распространяется. Фаза колебаний зависит
не только от времени, но и от координаты.
волновой процесс есть, волна
распространяется. Фаза колебаний зависит
не только от времени, но и от координаты.
 коэффициент фазы,
аналогичен волновому числу k, только
используется в направляющих системах.
Таким образом, условия распространения
электромагнитной волны по волноводу:
коэффициент фазы,
аналогичен волновому числу k, только
используется в направляющих системах.
Таким образом, условия распространения
электромагнитной волны по волноводу:

К ритическая
длинна волны зависит от типа волновода:
формы, размеров, типов волны.
ритическая
длинна волны зависит от типа волновода:
формы, размеров, типов волны.
Если заданы параметры волновода, то для того чтобы обеспечить условия распространения ЭМВ необходимо выполнить условия .
На практике стараются передавать ЭМ энергию одним типов волн. Поэтому необходимо выполнить условие для основной волны и не выполнить для волн высших типов. Это можно выполнить если рабочей волной будет волна с наибольшее критической длинной. Волна у которой критическая длина волны максимальна называет основной волной, все остальные носят название волн высших типов.(рис 5.7).
Поперечное волновое сопротивление
Волновое сопротивление это:

Рассмотрим условия:

Учтем:


 Рассуждая аналогично
получим:
Рассуждая аналогично
получим:
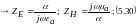 Т.к. есть мнимая
единица, волновод подобен реактивной
нагрузке, следовательно, переда энергии
по волноводу невозможна.
Т.к. есть мнимая
единица, волновод подобен реактивной
нагрузке, следовательно, переда энергии
по волноводу невозможна.
 волнового процесса
нет.
волнового процесса
нет.
График зависимости
Z от


Длина волны в волноводе
Длинной волны в
волноводе называют расстояние между
двумя ближайшими точками вдоль оси
волновода, фазы колебаний которых
отличаются на
 .
В соответствии с данным определением
.
.
В соответствии с данным определением
.
 полная
фаза
полная
фаза
Две точки:
 по определению
по определению

 -
длина волны в волноводе.
-
длина волны в волноводе.
( при совпадении длины волны в волноводе
и в свободном пространстве)
при совпадении длины волны в волноводе
и в свободном пространстве)

Фазовая скорость, скорость переноса энергии, групповая скорость
Фазовая скорость, скорость перемещения фазы гармонической волны.

Скорость переноса энергии характеризует движение энергии электрического
или магнитного полей.

Групповая скорость –скорость перемещения огибающей сигнала с ограниченным спектром. Это скорость перемещения волнового пакета, т.е. пакета, образованного группой волн.
 Скорость переноса
энергии и групповая скорость совпадают.
Скорость переноса
энергии и групповая скорость совпадают.
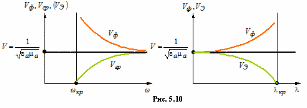
Таким образом: В волноводе имеет место волновой процесс при частоте , это необходимо учитывать при расчете волноводных линий передачи ЭМ энергии.
Энергетические параметры:
В реальном волноводе А поля падающей волны уменьшается по экспоненциальному закону:
 Мощность, переносимая
через поперечное сечение волновода:
Мощность, переносимая
через поперечное сечение волновода:

 -длинна
волноводы.
-длинна
волноводы.
Отсюда КПД:

ТЕМА №6. ПРЯМОУГОЛЬНЫЕ ВОЛНОВОДЫ
